42. Синтез управляющего устройства оптимальной по быстродействию системы методом фазовой плоскости.

По фазовому портрету можно судить об устойчивости и характеру переходных процессов системы. Метод исследования систем, основанный на построении их фазового портрета, называется методом фазовой плоскости. Достоинством метода фазовой плоскости является то, что он позволяет наглядно представить всевозможные процессы, происходящие в системе, и является точным, а не приближенным методом. Его недостатком является то, что он применим к системам второго порядка.

Фазовый метод:фазов простр-во,построен-е троекторий.

Основ-н на представ-ии о фазов простр-ве и представ-м динамики сист дв-ием точки в это простр-во.

В прост случае сист однокоординатная:

Для того чтобы знать как сист поведёт себя в будущ необход знать:

Полн опис-е сист-опис-е вых сигнала и n производных.

Постр n-мерное простр-во и сост-е сист в точку в этом n+-мерном простр-ве (двиг-ся только по непрерыв кривой).

Исследуя св-ва кривой(длину,кривизну) можно много узнать о повед-ие сист. n=2

Фаз траектория имеет направ-ие,т.к это послед отсчёты во времени.У люб траектории сущ-т определ правила:

1)в верх полупл-ти траектор может идти только слева-направо.В нижн-справа налево.

2)ось абсцисс может пересек только под прям углом.

3)сколь бы не сложна была троект-ия,будучи опред-ой для одной и той же сист при одних и тех же усл-ях троект-ия не может пересечь сама себя.Если это произошло знач проекция троект-ии в фаз простр-ве(не все пар-ры сист истены, она не изучена).

Прост-во больш разм-ти услож-ет постр-ие траектории.

В этих случ-х точка будет устойч фокусом.

Траектор могут иметь узлы-устойч и неустойч.Узлы получ-ся в периодич движ-ии.

Фокусы получ-ся в периодич движ-ии.

43. Вариационное исчисление и основные задачи вариационного исчисления. Перечислите основные задачи вариационного исчисления?

Вариационное исчисление разрабатывает методы, позволяющие находить максимальные и минимальные значения функционалов.Это один из методов для нахождения оптимального управления.

Методы вариационного исчисления позволяют найти условия, при которых достигается экстремум критерия оптимальности записанного в виде некоторого функционала, Условия получаются в виде некоторой системы уравнений относительно управления и переменных состояния ОУ фазовых координат объекта.

Функционал – переменная величена x зависящая от функции Ui(t), i(t), yj(t), j(t), i=; j=

Приращение или вариация бU_i аргумента U2(t) функционала есть разность функция из класса функций Ui(t)/

Первая вариация функционала:

Вторая вариация функционала:

Необходимым условием существования экстремума непрерывного функционала является равенство 0 его первой вариации х=0.

Вариационное исчисление применяется в задачах с закрепленными концами, подвижными концами в задачах Больца, Майера, Лагранжа

Д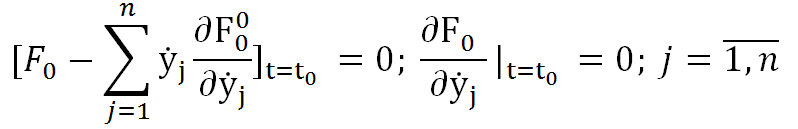ля этих двух задач необходимы условия сущ. Экстремума функционала кот. Должны быть дополнены условиями

К задачам вариационного исчисления относят задачи Больца, Майера, Лагранжа.

Оптимизация систем методом ВИ(вар. исч.) приводит к 2-ух точечной краевой задачи. Обычно решается в числин. форме методом последов.приближения. Задаем нач.условия и решаем уравнение Эйлера-Лагранжа, затем берут другие н.у. до тех пор, пока не попадем в задан.интервалы. данный способ малоэффективен.

Более эффективны методы: Метод максимума Потрягина (вышел из закона Маера. Но управл.воздействие – ограничено) и Динамич.программирование.

Основные задачи управления:

Задача управления по минимуму интеграла (задача Лагранжа)

Задача оптимальности по быстродействию (задача Майера)

Задача оптимального управления с заданными ограничениями (задача Больца)

Оптимизация СУ при вариационном исчислении приводит к двуточечной краевой задачи, а аналитическое решение возможно только в исключительных случаях.

Законы оптимального управления:

-- з.у. конечным состоянием: определение допустимого воздействия. По которому за задан.время Т нач.состояние переходит в конеч.состояние. в котором одна или неск.совокуп. составляющих состояний преобретает вохможное большее или меньшее значение при физич.огрничениях на остальные.

-- з.у. для достижения максим.быстродействия: до х(t_f) за миним.время, т.е. min_u ∫dt (пределы интеграл от t0 до tf)

--- по минимуму интеграла: нужно минимизировать нек.интеграл.

Все эти законы – частные случаи оптим.управления по координате (одной пременной). Беллман вывел оптим.стратегию управления или ПРИНЦИП оптимальности БЕЛЛМАНА: оптим.стратегия управления обладает свойством – что в независимости от нач.условия (решения) последующие (решение и стратегия) должны быть оптимальны по отношению к 1-му решению.