47. Учет физических ограничений и множители Лагранжа (на примере)

В условии задачи оптимальности одного из качеств системы фигурируют некоторые ограничения других её свойств в виде заданной управляющей силы или мощности, заданного веса заданных интервалов возможного изменения характеристик регулятора и объекта и д.р..

Основные виды ограничений:

Ограничения на фазовые координаты и управление

Введение этих ограничений приводит к задачи в закрытой области, что может привести к возможности использовать классические вариационные методы.

Метод множителей Лагранжа, метод нахождения условного экстремума функции , где , относительно m ограничений , меняется от единицы до m .

Функция Лагранжа в виде линейной комбинации

Для получения реальных условий применяют ограничения, метод множителей Лагранжа, максимум или минимум функций от одного или нескольких ограничений или зависимости задающего ограничения сложны для последовательного исключения. Делают ненужными реш. ур. опред. ограничения P(U)=P(U₁, U₂,...U_N), ограничение вида: Q(U)=Q(U₁, U₂,...U_N)≤C (2).

Например U_i² ≤ C_i,тогда исключительный вектор управления (Исходный критерий) G(U)=P(U)+ ^T Q(U), где ^T вектор столбец множителей Лагранжа.

U(λ)=U(λ₁, λ₂, …, λ_n ) (1)

Подставив (1) в (2) получим уравнение для определения множителей Лагранжа.

48. Обобщенная задача оптимального управления.

Оптимальное управление — раздел математики, изучающий неклассические вариационные задачи

Обобщенная задача оптимального управления – определение лин по отношению к одной единственной переменной с помощью процедуры инвариантности, вложение вводится доп. переменная .

Задача максимального быстродействия ,

Управление конечным состоянием

По минимуму интеграла:

49. Принцип максимума Понтрягина.

Принцип максимума Понтрягина гласит, что для оптимальности системы, т.е. для получения минимума функционала

(где x – переменные, относящиеся к заданной части системы, включающей в себя

регулируемый объект и не изменяемую в процессе синтеза часть регулятора;

переменные u выражают воздействие проектируемой части регулятора на заданную

часть системы – управления) необходимо существование таких ненулевых

непрерывных функций ₀(t)…_n(t), что при любом t[t₀; t₁], величина H, как функция переменных u₁...u_n, в заданной области их допустимых значений достигает максимума H=M(₀, . . . . , _n; x₀, . . . ., x_n) причем ₀ и M постоянны во времени и ₀ ≤0 и M=0

Этот принцип позволяет решать важные с практической точки зрения задачи, такие, как перевод космического корабля с одной орбиты на другую таким образом, чтобы расход топлива был минимален. Принцип максимума позволил решить многие проблемы оптимизации форм конструкций на основе вариационных подходов.

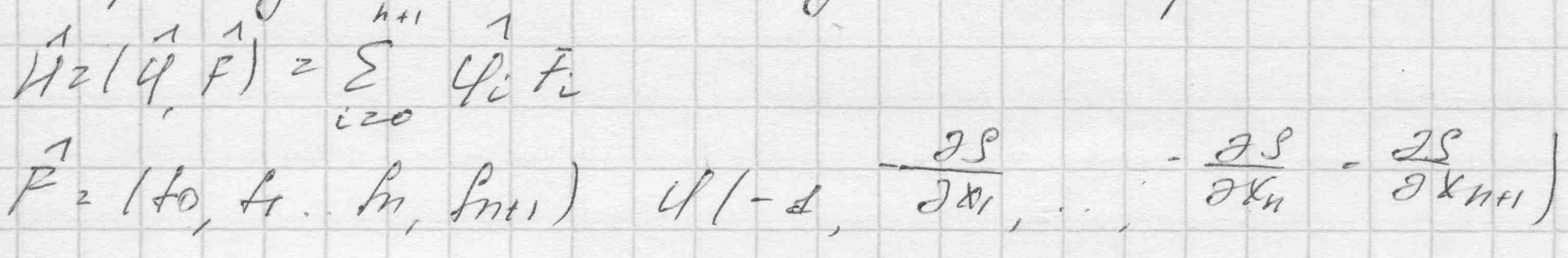
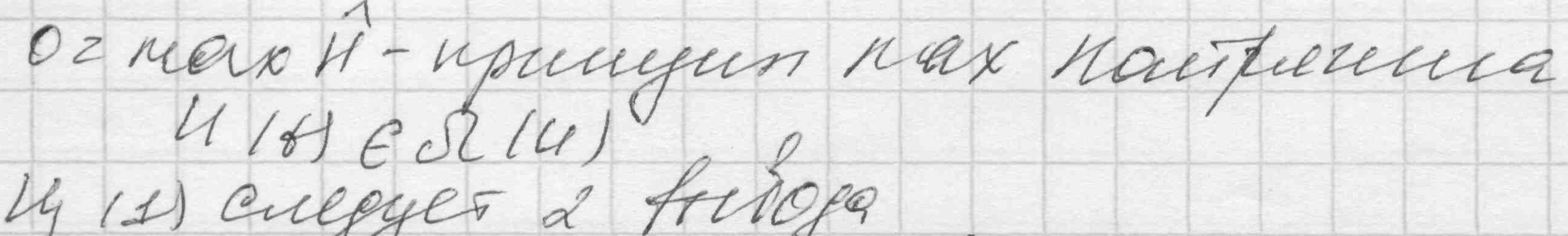
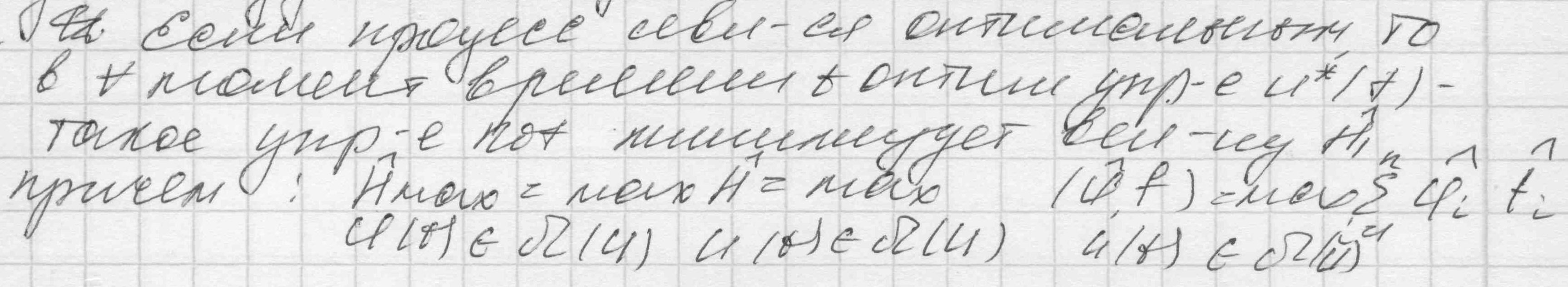
50. Метод динамического программирования Беллмана.

Динамическим программированием называют разработанный Беллманом метод оптимизации многошаговых процессов различной природы. Основу динамического программирования как метода оптимизации составляют:

1. принцип оптимальности;

2. инвариантное погружение, то есть включение исходной задачи в семейство аналогичных задач;

3. функциональное уравнение, получаемое на основе принципа оптимальности и инвариантного погружения.

Основная идея метода динамического программирования заключается в следующем. Вместо того, чтобы решать исходную задачу, ее включает в некоторое семейство задач оптимизации (инвариантное погружение). При этом может оказаться, что между отдельными задачами существуют простые соотношения и среди задач семейства найдется такая, которая легко решается. Тогда, используя решение последней и соотношение, связывающие отдельные задачи семейства, то есть функциональное уравнение, получают решение исходной задачи.

Пусть требуется найти минимум функции:

Здесь - прямое произведение областей (множеств) определения функции

Рассмотрим семейство задач

где

Исходная задача погружена (инвариантное погружение) в построенное семейство задач в том смысле, что она входит в это семейство как частный случай при m = n. В задаче параметр m можно рассматривать как дискретное время. Введем в рассмотрение функцию Эту функцию называют функцией Беллмана.

Очевидно, справедливо следующее соотношение

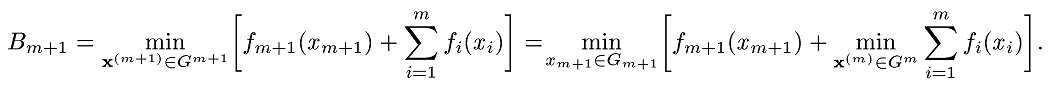
Но второе слагаемое в последнем выражении есть Bm, поэтому получаем следующее функциональное уравнение:

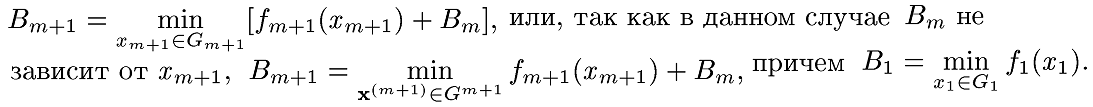
Это уравнение называют уравнением Беллмана. Решая его с учетом последнего условия, получим

Решением исходной задачи являются

Как видно, метод динамического программирования сводит задачу минимизации скалярной функции от n переменных к n задачам минимизации скалярных функций от одной переменной. В результате при числовом решении задачи существенно сокращается объем вычислений.

Принцип оптимальности Беллмана.

Оптимальная стратегия (поведение) обладает тем свойством, что, каковы бы ни были начальное соотношение и решения на начальном этапе, решения на последующем этапе должны составлять оптимальную стратегию относительно состояния, которое получается в результате принятия решений на начальном этапе.

В задачах оптимального управления оптимальность определяется функционалом (критерием оптимальности)

состояние – фазовым вектором x(t), стратегия – это управление u(t) на всем интервале решение – это выбор конкретного управления. Для задачи оптимального управления справедлив принцип оптимальности, если она обладает марковским свойством. По определению задача оптимального управления обладает марковским свойством, если после выбора управления на начальном интервале каково бы оно ни было, на величину критерия на конечном интервале оказывает влияние выбор управления на этом интервале и значение фазового вектора в конце начального интервала, то есть