
Матика 2 курс / Дифференциальные уравнения 2б
.pdf
1
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
«Кузбасский государственный технический университет»
Д.В. Алексеев, Г.А. Казунина, Н.В. Трушникова, Н.М. Латыпова
МАТЕМАТИКА: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
С ЭЛЕМЕНТАМИ ТЕОРИИ УСТОЙЧИВОСТИ
Рекомендовано в качестве учебного пособия учебно-методической комиссией специальности
140604 «Электропривод и автоматика промышленных установок и технологических комплексов»
Кемерово 2010

2
|
Рецензенты: |
|
|
Жирнова Т.С.доцент |
кафедры |
Математики |
|
Завьялов В.М., председатель |
УМК специальности |
140604 |
|
« Электропривод и автоматика промышленных установок и технологических комплексов»
Алексеев Дмитрий Валентинович, Казунина Галина Алексеевна, Трушникова Надежда Васильевна, Латыпова Наталья Минхадеевна. Математика: дифференциальные уравнения с элементами теории устойчивости: учеб. пособие [электронный ресурс]: для организации самостоятельной работы студентов специальности 140604 « Электропривод и автоматика промышленных установок и технологических комплексов»/ Г.А. Казунина.- Электрон.дан.- Кемерово: КузГТУ, 2010.- 1 электрон. опт. диск (CDROM); 3в.; цв.; 12 см. – Систем. требования: Pentium IV; 0348 Мб; Windows 97-03; (CD-ROM дисковод); мышь. Загл. с экрана.
Последовательно и доступно изложен теоретический материал по обыкновенным дифференциальным уравнениям с элементами качественной теории дифференциальных уравнений и теории устойчивости для линейных и нелинейных систем согласно государственному образовательному стандарту и рабочим программам по дисциплинам « математика» и «специальные главы математики» для специальности 140604 « Электропривод и автоматика промышленных установок и технологических комплексов». Теоретические положения сопровождаются большим количеством подробно разобранных задач.
ГУ КузГТУ
Алексеев Д.В. Казунина Г.А.
Трушникова Н.В. Латыпова Н.М.

3
ВВЕДЕНИЕ
Обыкновенные дифференциальные уравнения - главный мост,
связывающий математику и ее приложения в технике и естествен-
ных науках.
Теория дифференциальных уравнений позволяет изучать все-
возможные процессы эволюции состояния изучаемой системы (во времени или в пространстве). В зависимости от конкретной иссле-
дуемой системы может встретиться один из двух принципиально различных случаев:
-число переменных, задание которых полностью определяет состояние системы, конечно;
-число переменных, задающих состояние системы, бесконеч-
но.
Второй случай является предметом теории дифференци-
альных уравнений в частных производных и далее не рассмат-
ривается. Первый случай служит предметом изучения излагаемой ниже теории обыкновенных дифференциальных уравнений.
Важность теории дифференциальных уравнений для приложе-
ний продиктована тем, что подавляющее большинство законов природы описывается математическими равенствами, содержа-
щими искомую функцию и ее производные. Например, закон
движения Ньютона
m |
d 2 X (t) |
F(X (t),t) , |
(B.1) |
|
|||
|
d t 2 |
|
|

4
связывает искомую вектор-функцию, положение частицы X(t), и ее
d 2 X
вторую производную по времени |
|
|
- ускорение, а закон радио- |
||||
|
dt 2 |
||||||
|
|
|
|
|
|
|
|
активного распада |
|
|
|
|
|
||
|
dN(t) |
|
- kN(t) |
(B.2) |
|||
|
dt |
||||||
|
|
|
|
|
|
||
- искомую функцию N(t), |
|
число нераспавшихся ядер, |
и их |
||||
dN (t)
производную по времени dt .
Равенства вида (В.1), (В.2) называются обыкновенными диф-
ференциальными уравнениями (строгое определение дается ниже).
ФАЗОВЫЕ ПРОСТРАНСТВА,
ФАЗОВЫЕ ТРАЕКТОРИИ И ИНТЕГРАЛЬНЫЕ КРИВЫЕ
Пусть состояние изучаемой системы полностью характеризу-
ется (в фиксированный момент времени) упорядоченным набором n функций X1 (t), X2 (t),…,Xn (t). Их можно считать координатами точки M (t) в n - мерном пространстве, положение которой и задается радиус-вектором X (t) = (X1 (t), X2 (t),…,Xn (t)).
Таким образом, имеем соответствие:
{состояние системы} {точка в пространстве}.
Пространство, точки которого изображают состояние систе-
мы, называется фазовым пространством.
В процессе эволюции системы точка в фазовом пространстве

5
совершает движение, описывающее изменение состояния системы.
Траектория точки в фазовом пространстве называется фазовой траекторией системы. Следовательно, фазовая траектория системы
задается некоторой вектор - функцией X (t) скалярного аргумента,
времени t.
Производная вектор-функции dX / dt X t , как хорошо из-
вестно, есть вектор скорости V, который является касательным век-
тором к траектории, годографу вектор - функции. Когда говорят о фазовом пространстве вектора скорости, принято использовать термин «фазовая скорость».
В общем случае фазовая скорость является функцией как состояния системы, так и времени, то есть V (X ,t). Такие функции называют векторным полем.
Задача теории обыкновенных дифференциальных уравнений – отыскание фазовой траектории системы по известному полю скоростей V (X ,t). Следовательно, значение в
фиксированный момент времени отождествляется с производной dX t / dt :
|
dX (t) |
V X ,t . |
(B.3) |
|
d t |
||
|
|
|
|
Определение B.1. |
|
|
|
Равенство (В.3), связывающее траекторию точки |
X t , изоб- |
||
ражающей состояние системы в n-мерном фазовом пространстве, с n-мерным полем скоростей V (X ,t) называется дифференциаль-
ным уравнением порядка n.

6
Определение В.2.
Вектор-функция (t) , удовлетворяющая уравнениям:
d (t) |
V ( (t),t) ; |
(t |
) a const , |
(В.4) |
|
dt |
|||||
|
0 |
|
|
||
|
|
|
|
называется решением дифференциального уравнения (В.3) с
начальным условием (t0 ) a .
Иногда для геометрической интерпретации решений диффе-
ренциальных уравнений бывает удобно расширить фазовое про-
странство на одно дополнительное измерение, добавив дополни-
тельную координату - время. Построенное таким образом n +1 -
мерное пространство, состоящее из точек X t , t , называется рас-
ширенным фазовым пространством.
Траектория состояния системы в расширенном фазовом про-
странстве называется интегральной кривой дифференциального
уравнения.
Суммируем изложенное:
-эволюция системы, описываемой обыкновенным диффе-
ренциальным уравнением, геометрически изображается движением точки в фазовом пространстве - фазовой траекторией, или в расши-
ренном фазовом пространстве - интегральной кривой;
-решить дифференциальное уравнение - значит найти фа-
зовую траекторию системы по заданному полю скоростей и извест-
ному начальному состоянию системы.

7
СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
При заданном поле направлений V X ,t при решении диффе-
ренциального уравнения (В.3) могут возникнуть две принципиаль-
но различные ситуации:
-различным начальным состояниям системы соответ-
ствуют непересекающиеся фазовые траектории (и интегральные кривые), т. е. через заданную точку фазового пространства прохо-
дит единственная фазовая траектория;
-фазовые траектории (интегральные кривые) могут пере-
секаться.
На вопрос - какой из указанных случаев реализуется - дают ответ теоремы существования и единственности решений, кото-
рые являются следствием следующей основной теоремы.
Основная теорема о выпрямлении поля направлений.
Гладкое (т. е. дифференцируемое по всем своим переменным)
поле направлений V (X ,t) в окрестности любой точки X 0 ,t0 может быть преобразовано в поле параллельных направлений преобразо-
ванием координат Y Ф(X ,t) . Другими словами исходное уравне-
ние
dX (t) |
V (X ,t), |
X (t |
) X |
|
(В.5) |
|
0 |
||||
dt |
0 |
|
|
||
|
|
|
|
||
переводится в уравнение
|
|
|
|
8 |
|
|
|
|
|
|
|
dY |
0, |
Y (X |
|
,t |
|
). |
(В.6) |
||
|
|
0 |
0 |
|||||||
|
dt |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Смысл теоремы |
понятен: |
преобразование |
координат |
|||||||
Y X ,t устанавливает в окрестности точки ( X 0 , t0 ) |
расширенно- |
|||||||||
го фазового пространства соответствие между интегральными кри-
выми уравнения (В.5) и прямыми линиями, параллельными оси t,
интегральными кривыми уравнения (В.6). Однако, отыскание явно-
го вида преобразования координат Y X ,t эквивалентно реше-
нию исходного уравнения в явном виде (В.5) и является иногда за-
труднительным.
Важность данной теоремы состоит в том, что в случае выпол-
нения ее условий, гарантирующих непересечение фазовых траекто-
рий и интегральных кривых, можно на качественном уровне анали-
зировать общий вид решений дифференциальных уравнений, не прибегая непосредственно к аналитическому решению. Это осо-
бенно важно в тех случаях, когда исходное уравнение не может быть решено в замкнутой форме через известные функции и воз-
можно лишь его численное решение на ЭВМ.

9
1. АВТОНОМНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Автономным уравнением первого порядка называется уравне-
ние
dX (t) |
V ( X ) , |
(1.1) |
|
dt |
|||
|
|
где X - обычная (скалярная) функция времени t.
Фазовое пространство такой системы - прямая линия (число-
вая ось ОХ), расширенное фазовое пространство - (t, X ) - плоскость,
фазовая траектория - отрезок фазовой прямой, интегральная кривая
- линия на плоскости (t, X ).
Фазовая скорость (поле направлений) V (X ) зависит только от состояния системы - положения точки на фазовой прямой. Если функция V (X ) дифференцируема - поле направлений гладкое.
ПРИМЕР 1.1. Проанализировать решение уравнения
|
dX |
= - (X - a)(X - b), b>a > 0 , |
(1.2) |
|
|
||
|
d t |
|
|
в зависимости от начального состояния X0. |
|
||
Поле направлений V - (X - a)(X - b) - |
дифференцируемая |
||
функция. Согласно основной теореме, фазовые траектории и инте-
гральные кривые не пересекаются.
Постоянные |
( ) |
= b - решения уравнения (1.2), в |
X t a и X t |
чем легко убедиться прямой подстановкой. Их фазовые траектории
- точки на фазовой оси, а интегральные кривые - прямые, парал-
10
лельные оси Ot.
При X < a фазовая скорость V < 0 и точка, изображающая со-
стояние системы, удаляется от положения равновесия X = a. Соот-
ветствующая фазовая траектория - луч, направленный от начального положения к , , X 0 , X 0 a .
При a X b фазовая скорость положительна и точка, изоб-
ражающая состояние системы, удаляется от точки X = a, прибли-
жаясь к точке X = b, но не достигая его. Фазовая траектория - полу-
открытый интервал фазовой оси X0, b , a X0 b .
При X b фазовая скорость отрицательна и состояние при-
ближается к равновесному (X b). Фазовая траектория - полуот-
крытый интервал (b, X 0 ], |
X o b . |
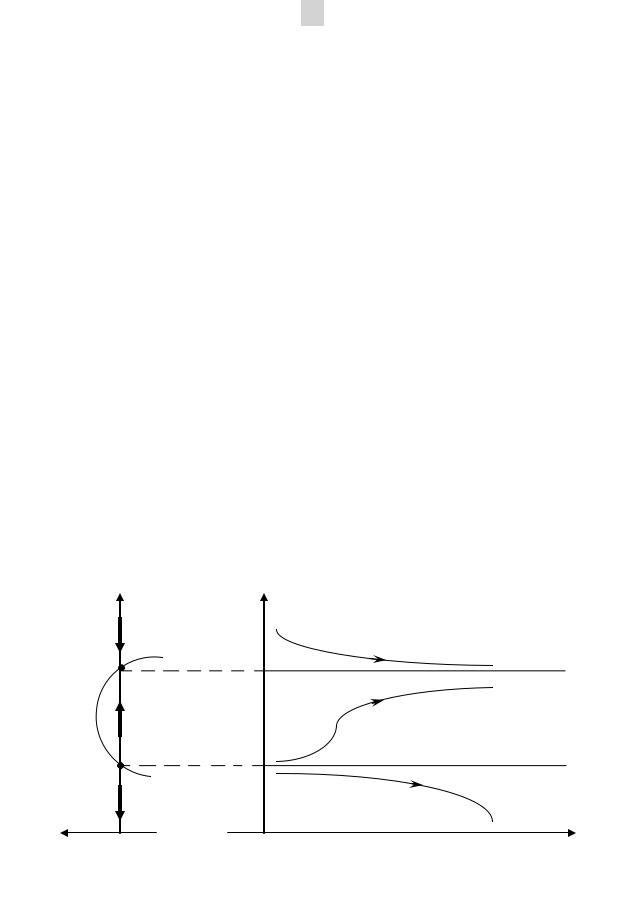
Качественный вид интегральных кривых и фазовые траекто- |
|
рии приведены на рисунке 1.1. |
|
x |
x |
|
x b |
x a
V |
t |
a) |
á) |
Рис.1.1. Качественное описание решений уравнения (1.2):
а)- фазовое пространство; б)- расширенное фазовое пространство
