
Матика 2 курс / Дифференциальные уравнения 2б
.pdf
91
координат ( Det A 0 ), то в окрестности этой точки фазовые портреты системы и фазовые портреты ее линеаризации каче-
ственно эквивалентны, если только неподвижная точка не явля-
ется «центром».
Если неподвижная точка линеаризации является «центром», то фазовый портрет исходной нелинейной системы будет «центром» или «фокусом». Для наличия «центра» необходимо, чтобы фазовые траектории исходной системы имели ось симметрии, проходящую через неподвижную точку. Последнее требование равносильно тре-
бованию того, чтобы уравнение
V1(x1, x2 ) dx1 V2 (x1 , x2 ) dx2
не изменилось при замене x1 на -x1 (или x2 на x2 ).
ПРИМЕР 3.15. Исследовать устойчивость решения нелинейной системы
dx1 |
|
e |
( x x |
|
) |
x2 |
|
|
|
|
1 |
2 |
|
||
dt |
|
||||||
|
|
|
|
|
|
|
|
dx2 |
|
x1 x1x2 |
|||||
|
|
|
|||||
dt |
|
|
|
|
|
|
|
вблизи неподвижной точки.
Решая систему уравнений
e(x1 x2 ) x2 0
x1 x1x2 0,
находим, что неподвижной точкой системы является точка
x1 1.x2 1

92
Рассмотрим отклонение системы от положения равновесия, вводя новую переменную
|
|
|
|
|
|
|
u1 |
|
x1 |
1 |
. |
||
|
|
|
|
|
|
|
|
|
|
x2 |
|
||
|
|
|
|
|
|
|
u2 |
|
1 |
||||
Подставляя |
x |
u |
1; x |
u |
2 |
|
1 в исходную систему, получаем |
||||||
|
1 |
1 |
2 |
|
|
|
|
|
|||||
|
du |
e u1 u2 u |
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|||
|
dt |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
||||
|
du2 |
u1 1 (u2 1)(u1 1) u1u2 u2 |
|||||||||||
|
|
|
|
||||||||||
|
dt |
|
|
|
|
|
|
|
|
||||
Далее можно использовать разложение Маклорена для показатель-
ной функции с точностью до бесконечно малых первого порядка e u1 u2 ~ 1 u1 u2.
И, оставляя во втором уравнении только линейное слагаемое, полу-
чаем линеаризацию системы
|
du |
|
|
|
|
|
||
|
1 |
u |
|
|
1 |
0 |
||
|
|
|
||||||
dt |
1 |
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
; |
A |
|
. |
||
|
du2 |
|
u2 |
|
0 |
1 |
||
|
|
|||||||
dt |
|
|
|
|
|
|||
Заметим, что линеаризацию можно получить по формуле (3.36)
|
|
x1 x2 |
e |
x1 |
x2 |
|
|
1 |
0 |
|
A e |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
x1 |
|
x 1 |
0 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
Характеристики матрицы |
|
|
|
|
|
|
|
||
A : SpA 0; |
DetA 1 0; |
1 |
1; |
2 |
1свидетельствуют о |
||||
том, что неподвижная точка x1 1; x2 |
1 исходной нелинейной |
||||||||

93
системы и ее линеаризации является неустойчивым положением равновесия. Фазовый портрет относится к типу «седло».
ПРИМЕР 3.16. Рассмотрим систему
dq |
p q (q2 p2 ) |
|
|
dt |
|
||
|
|
|
|
dp |
|
, |
(3.37) |
q p (q2 |
p2 ) |
|
|
dt |
|
||
|
|
|
|
используя переход к полярным координатам на (q, p) – плоскости: q cos
p sin . |
(3.38) |
Покажем, что поведение исходной системы и системы, получаемой
линеаризацией около положения равновесия |
p q 0 , различно. |
||||||||||||||||||||||
Используя формулы дифференцирования |
|
|
|||||||||||||||||||||
|
|
|
dq |
cos |
d |
|
sin |
d |
|
|
|
|
|||||||||||
|
|
|
dt |
dt |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|||||||||||
|
|
|
dp |
sin |
d |
|
cos |
|
d |
, |
(3.39) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dt |
|
dt |
|
dt |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и подстановку (3.38), (3.39) в (3.37) получаем |
|
||||||||||||||||||||||
cos |
d |
|
sin |
d |
|
sin 3сos ; |
|||||||||||||||||
dt |
dt |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin |
d |
|
cos |
d |
|
cos 3 sin . |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||
Умножая первое из этих уравнений на sin , |
а второе на cos с |
||||||||||||||||||||||
последующим вычитанием, а затем, умножая первое уравнение на cos , а второе на sin споследующим сложением,
приводим систему к виду

94
d 3 dt
|
d |
|
. |
(3.40) |
|
|
|||
dt |
|
|
Положение равновесия системы (3.37 , 3.40) - 0 (это следует из приравнивания к нулю d / dt и d / dt ).
Нелинейная система имеет при 0 вид
d 3 dt
d 1 , dt
а линеаризованная система
d 0 dt
d 1. dt
Фазовые траектории линеаризованной системы - окружности по-
стоянного радиуса const, t C , а фазовые траектории точной системы - скручивающиеся спирали (рис. 3.14):
|
d |
|
|
1 |
|
1 |
|
|||||
|
|
t ; |
|
2 t ; |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
3 |
2 |
|
2 |
||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
; |
|
t C; t 0. |
||||
|
|
|
|
|
|
|||||||
|
1 2 2 |
|
|
|||||||||
|
|
|
t |
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
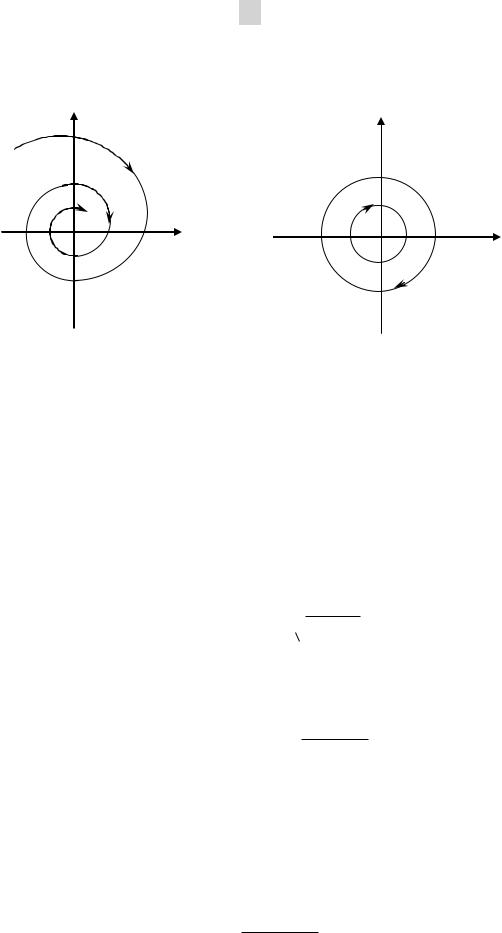
95
p |
p |
q |
q |
а) |
б) |
Рис. 3.14. Фазовые траектории точной (а) и линеаризованной (б)
системы (3.37).
ЗАДАЧА 3.10. Исследуйте на устойчивость нулевое решение системы
dx1 / dt ln( 4x2 e 3x1 ) dx2 / dt 2x2 1 3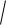 1 6x1 .
1 6x1 .
ЗАДАЧА 3.11. При каких значения параметра а нулевое ре-
шение системы будет асимптотически устойчиво?
dx1 / dt 2e x1 
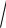 4 ax2 dx2 / dt ln(1 9x1 ax2 ).
4 ax2 dx2 / dt ln(1 9x1 ax2 ).
ЗАДАЧА 3.12. Найдите положение равновесия системы и ис-
следуйте на устойчивость
dx1 / dt ex2 ex1 dx2 / dt 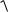
 3x1 x22 2.
3x1 x22 2.

96
ЗАДАЧА 3. 13. Покажите, что нулевое решение системы
dx1 / dt x1 cos x2 e x3
dx2 / dt sin x1 ln(1 x2 ) x1x32 dx3 / dt x12 cos x3 x2 sin x3
асимптотически устойчиво при 2 ; |
0. |

97
4. ПРИМЕРЫ АНАЛИЗА НЕЛИНЕЙНЫХ УРАВНЕНИЙ ПОРЯДКА п 2
Отличительной чертой нелинейных уравнений порядка п 2
является существование решений весьма необычного характера -
автоколебательных и хаотических режимов.
В автоколебательном режиме система независимо от началь-
ного состояния по истечении определенного времени начинает со-
вершать колебания с частотой и амплитудой, которые не зависят от начального состояния системы и определяются только исходными динамическими уравнениями. Следовательно, в таких системах ко-
нечное состояние эволюции может быть предсказано однозначно по исходным уравнениям.
В противоположность автоколебаним, в хаотическом режиме
конечное состояние системы становится принципиально непредска-
зуемым, и задачей теории является установление того, при каких значениях параметров исходного уравнения система переходит в хаотический режим.
Следует отметить, что законченной теории описанных режи-
мов в настоящее время не существует, а методы их исследования весьма разнообразны и часто зависят от рассматриваемого уравне-
ния.
Тем не менее, представляется целесообразным рассмотреть эти режимы во вводном курсе на простейших примерах по следу-
ющим причинам.

98
Во-первых, как автоколебания, так и хаос встречаются в реа-
листических моделях разнообразных явлений естествознания и ин-
женерной практики, когда исследуемая система является открытой,
то есть обменивается с окружением энергией (а в химических реак-
циях и веществом). Следовательно, будущим инженерам совер-
шенно необходимо знать о существовании данных явлений.
Во-вторых, исследование автоколебаний и хаоса позволяет в полной мере ощутить необходимость и полезность рассмотренных выше качественных методов, поскольку в этих случаях точные ана-
литические решения подучены быть не могут, а качественные ме-
тоды позволяют построить достаточно полную картину возникаю-
щего режима в этих далеко нетривиальных случаях.
4.1. ОСЦИЛЛЯТОР ВАН ДЕР ПОЛЯ
Осциллятор Ван дер Поля
d |
2 |
x |
|
|
|
x |
2 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
dx |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x 0 |
(4.1) |
|
dt |
2 |
A |
2 |
|
|
|||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|||||
является одной из простейших систем, описывающих режим авто-
колебаний. В отсутствии «затухания» 0 , уравнение (4.1)
описывает обычные гармонические колебания с частотой , а в
линейном режиме А2 , |
0 |
- затухающие колебания. |
|
В общем случае |
0, |
А2 |
нелинейное «трение» |
(x2/А2 -1) dx / dt моделирует |
обмен |
энергией между колеба- |
|

99
тельной системой и окружающей средой.
Уравнение (4.1) удобно изучать после перехода к безразмер-
ным координатам
q |
x |
; |
t , |
|
|
(4.2) |
|||
|
A |
|
||
|
|
|
||
полагая dq / dt dq / d и / . После перехода к безразмер-
ным переменным (4.2) уравнение Ван дер Поля можно стандарт-
ным образом переписать в виде
dq |
p , |
(4.3) |
|
d |
|||
|
|
dp p(1 q2 ) q. d
ЗАДАЧА 4.1. Осуществите переход от (4.1) к (4.3).
В линейном случае 0 , уравнение (4.3) принимает вид
dq p , d
dp q. d
Его фазовые траектории – окружности
p2 q2 2E
с центром в положении равновесия q p 0 . Они являются ли-
ниями постоянного уровня интеграла энергии
H |
p2 |
q2 |
. |
|
|
|
(4.4) |
||
|
2 |
|||
|
|
|
||
|
|
|
|
В случае 0 линеаризованное уравнение (4.3) имеет не-

100
устойчивое положение равновесия – фокус q p 0 . Это следует непосредственно из решения уравнений
dq p, d
dp p q. d
Рассмотрим случай слабой нелинейности 0 1 . Для ана-
лиза характера решения рассмотрим, как изменяется энергия си-
стемы за один цикл колебаний.
Дифференцируя (4.4) по τ и используя уравнение движения
(4.3) получаем, что
(4.5)
то есть скорость изменения энергии пропорциональна ε. Поскольку
ε << 1, можно считать, что p и q могут быть представлены в виде суммы решений: соответствующего 0 линейного решения и зависящих от поправок
q a sin( ) q1 ,
p a cos( ) p1 . |
(4.6) |
|
Следовательно, исследуя изменение энергии за цикл в линейном по случае, можно в выражение (4.5) подставить в качестве p и q решения линейного уравнения (4.6):
dH |
a2 cos2( )(1 a2 sin2( )) o( 2) |
|
|
(4.7) |
|
d |
. |
|
|
|
Усредняя (4.7) по периоду, получаем:
