
Матика 2 курс / Дифференциальные уравнения 2б
.pdf
31
d |
2x |
|
dx |
|
|
|||
|
|
2 |
2 |
|
2 |
x |
2 |
0 . |
|
|
2 |
|
|||||
d t |
|
|
d t |
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
Фазовое пространство системы (2.16) – плоскость (x1, x2), рас-
ширенное фазовое пространство - (x1, x2, t). При этом ось t перпен-
дикулярна фазовой плоскости.
Неподвижная точка (положение равновесия системы) x1= x2= 0 - начало координат фазовой плоскости, является особой фазовой траекторией. Соответствующая ей интегральная кривая - ось t в
пространстве.
Уравнение фазовой траектории, согласно (2.6) или (2.9), имеет
вид:
|
|
dx2 |
|
x2 |
|
(2.17) |
|
|
dx1 |
1 x1 . |
|||
|
|
|
||||
Вводя x2 / x1; |
dx2 / dx1 x1 d / dx1 , |
получаем урав- |
||||
нение d dx1 / x1, решением которого являются кривые ln( Cx1)
или x2 x1 ln( Cx1) . Полученные фазовые траектории образуют фа-
зовый портрет типа «неустойчивый вырожденный узел». Решение уравнения (2.17), записанное в виде
x2 ln x1 ln C const C1, x1
задает первый интеграл системы:
H (x , x ) |
x2 |
ln x |
const C , |
(2.18) |
|
|
|||||
1 |
2 |
x1 |
1 |
1 |
|
|
|
|
|
|
|
где значение С определяется начальным состоянием системы
32
x0
H0 2 ln x10. x10
Поэтому фазовые траектории - линии уровня функции H(x1,x2).
Направление движения точки по фазовой траектории при возраста-
нии параметра t определяется непосредственно по направлению
|
|
фазовой скорости V (x1)i |
(x1 x2 ) j в каждом квадранте фазовой |
плоскости. |
|
x2
V
x1
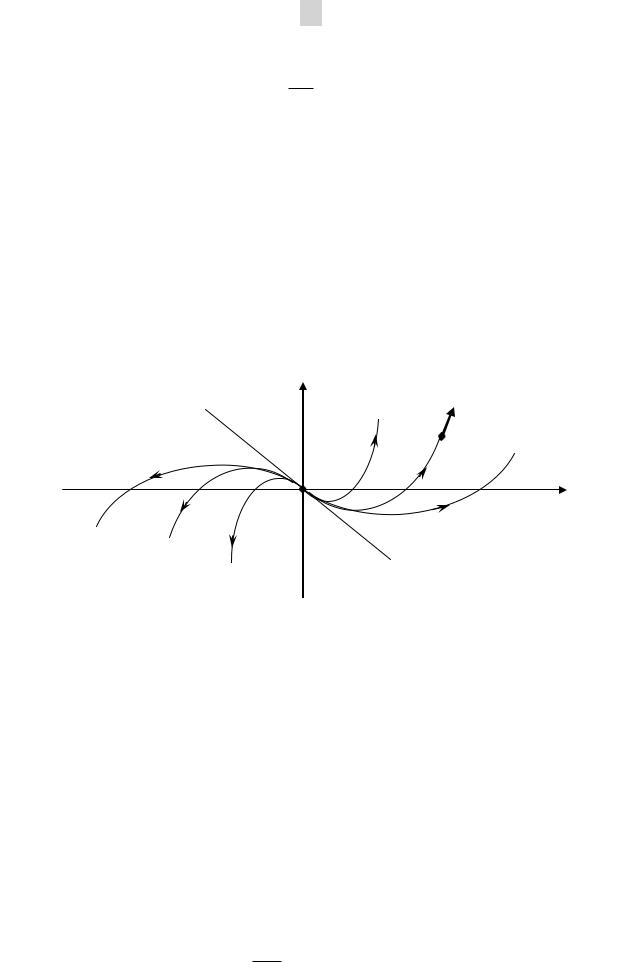
Рис. 2.2. Фазовые траектории системы (2.16) (фазовые портреты типа «неустойчивый вырожденный узел»)
Направление движения «от неподвижной точки» свидетель-
ствует о неустойчивом характере положении равновесия.
ЗАДАЧА 2.1. Показать, что
1. Уравнения фазовых траекторий системы dxdt1 x1
33
dx2 2x2 dt
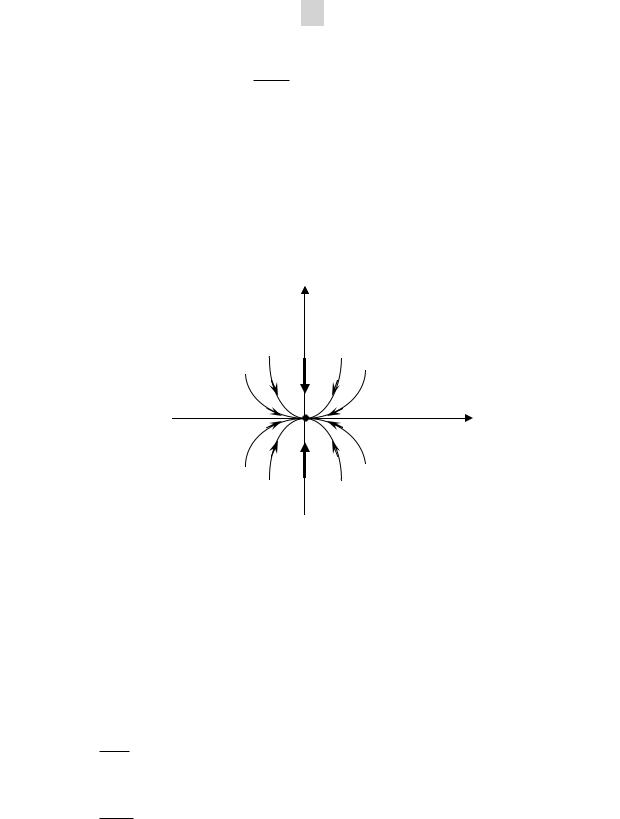
в окрестности неподвижной точки x1 = x2 = 0 имеют вид y = Cx2;
2.Первый интеграл системы H (x1, x2) = y / x2;
3.Фазовый портрет имеет тип «устойчивого узла» (рис 2.3).
x2
x1
Рис. 2.3. Фазовый портрет типа «устойчивый узел»
ЗАДАЧА 2.2. Показать, что
1. Уравнение фазовых траекторий системы dxdt1 x2
dx2 x1 dt
в окрестности неподвижной точки x1 = x2 = 0 имеет вид
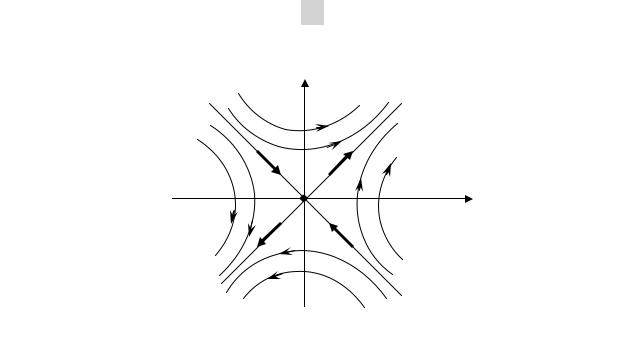
x22 – x12 = C;
2. Первый интеграл системы H (x1, x2) = x22 – x12; 3. Фазовый портрет имеет тип «седло» (рис 2.4).
34
x2
x1
Рис. 2.4. Фазовый портрет типа «седло»

35
3.ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
СПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
(Системы линейных дифференциальных уравнений)
3.1. ЭКВИВАЛЕНТНОСТЬ СИСТЕМЫ УРАВНЕНИЙ И ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
Рассмотрим однородную линейную систему дифференциаль-
ных уравнений второго порядка с постоянными коэффициентами
a11, a12, a21, a22:
dx1 a11x1 a12x2 d t
dx2 |
a |
21 |
x a |
22 |
x |
2 |
. |
(3.1) |
|
||||||||
dt |
1 |
|
|
|
||||
|
|
|
|
|
|
|
||
Покажем, что система (3.1) равносильна дифференциальному уравнению второго порядка. Выразим x 1 из второго уравнения си-
стемы:
x |
1 |
|
|
|
dx2 |
|
|
a22 |
x |
2 |
||||||||
|
|
|
|
|
||||||||||||||
1 |
|
a21 |
|
|
dt |
|
a21 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
dx1 |
|
1 |
|
d 2x2 |
- |
|
a22 |
|
dx2 |
|||||||||
|
|
|
|
|
|
|
||||||||||||
dt |
a |
21 |
|
|
dt |
2 |
|
|
|
a |
21 |
|
|
dt |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и подставим в первое уравнение. Тогда первое уравнение примет вид

36
d |
2x |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
2 |
- (a |
a |
22 |
) |
2 |
(a a |
22 |
- a |
a |
21 |
)x 0, |
(3.2) |
|
|
|
|
|||||||||||
dt |
2 |
11 |
|
|
dt |
11 |
12 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то есть является дифференциальным уравнением второго порядка с постоянными коэффициентами.
ПРИМЕР 3.1. Записать систему
dx1 |
2x |
x |
|
|
|
||
dt |
1 |
2 |
(3.3) |
|
|
dx2 x1 dt
в виде эквивалентного ей дифференциального уравнения.
Выражая x1, dx1 /dt из второго уравнения и подставляя в пер-
вое, имеем:
|
dx |
|
dx |
d |
2x |
d |
2x |
dx |
|
|
||||||
x |
2 |
, |
1 |
|
|
|
2 |
, |
|
|
2 |
2 |
2 |
x |
2 |
0. |
|
|
|
|
|
|
|
|
|
||||||||
1 |
dt |
|
dt |
dt |
2 |
|
dt |
2 |
|
dt |
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Покажем, что дифференциальное уравнение второго порядка эквивалентно системе двух дифференциальных уравнений первого порядка с постоянными коэффициентами. Рассмотрим уравнение
d |
2x |
|
dx |
|
|
|
|
|
|
|
2 |
P |
2 |
P x |
2 |
0. |
(3.3a) |
|
|
|
|
|||||
dt |
2 |
1 |
dt |
0 |
|
|
||
|
|
|
|
|
|
|
||
Введем новую переменную dx2 / dt x1 , тогда
d 2x2 dx1 . dt 2 dt

37
Подставляя в исходное уравнение, получим
d |
2x |
|
dx |
|
|
|
|
2 |
2 |
|
|
|
|
|
P1 |
|
P0 x2 ; |
dt |
2 |
dt |
|||
|
|
|
|
||
dx1 |
- P x - P x |
. |
|
||
dt |
1 1 0 2 |
|
|
|
Тогда система, равносильная исходному уравнению, имеет вид
dx1 |
- P x - P x |
||
|
|||
dt |
1 1 |
0 |
2 |
|
|
(3.3б) |
|
dx2 x1. dt
ПРИМЕР 3.2. Найти систему дифференциальных уравнений,
эквивалентную уравнению
d 2x2 2 dx2 x2 0 . dt2 dt
Обозначая dx2 / dt = x1 ; d 2x2 / dt2 dx1 / dt , получаем: dxdt1 2x1 x2
dx2 x1. dt
38
3.2. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМЫ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
ПОНЯТИЕ КАЧЕСТВЕННОЙ ЭКВИВАЛЕНТНОСТИ
Системы дифференциальных уравнений c постоянными коэф-
фициентами удобно анализировать и записывать в матричной фор-
ме, вводя обозначения:
x1 |
(t) |
матрица - столбец неизвестных, |
X |
|
|
|
|
|
x2 |
(t) |
|
X dXdt
dx1(t)
dt
dx2 (t)
dt
матрица - столбец производных,
a11
A
a21
a |
|
|
12 |
|
матрица - коэффициентов системы (3.1). |
a22 |
|
|
|
|
Система дифференциальных уравнений (3.1) переписывается следующим образом:
dx1
dtdx2
dt
a
11
a
21
a |
x |
(t) |
|
12 |
1 |
|
|
a22 |
|
|
|
x2 |
(t) |
(3.4) |
dXdt AX .
ПРИМЕР 3.3. Линейное дифференциальное уравнение второго
порядка

39
|
|
|
|
|
|
|
|
|
|
|
d 2x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
2 |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
эквивалентно системе линейных уравнений |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx1 |
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
x |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
||
с матрицей коэффициентов A |
|
|
|
. Фазовыми траекториями |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
этой |
|
системы |
|
является |
семейство |
гипербол (см. задачу 2.2.) |
||||||||||||||
x 2 |
x |
2 C . |
Матрица системы имеет собственные значения |
|||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
и |
и 2 |
1 |
и |
может быть приведена к более простой мат- |
|||||||||||||||
рице |
|
|
|
1 |
|
0 |
|
|
в |
|
базисе |
|
|
из |
собственных |
векторов |
||||
|
J |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
e1 |
|
|
e2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
, |
|
|
|
При этом матрица перехода T |
(см. |
||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 1, пример 1.1). В новой системе координат исходная система уравнений принимает более простой вид
dXdt JX dxdt1 x1
dx2 x . dt 2
Исключив параметр t, получаем, что уравнение фазовых тра-
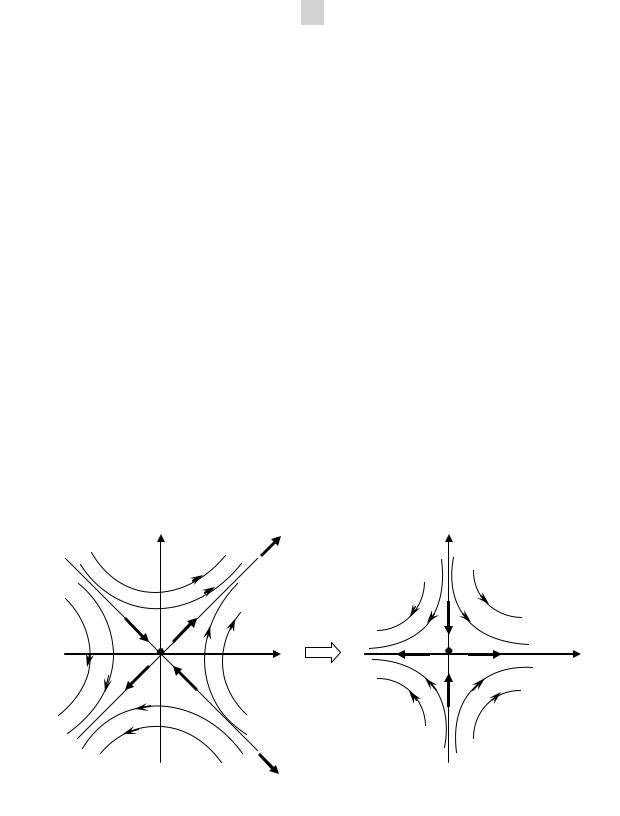
40
екторий имеет вид: x1x2 = C. Это также гиперболы. Но оси симмет-
рии этих гипербол повернуты на угол φ = π / 4 относительно осей
гипербол x12 x22 C .
Заметим, что характер фазового портрета в окрестности точки
(0; 0) (характер особой точки) сохраняется и является «седлом»
(рис. 3.1).
Две системы дифференциальных уравнений первого порядка называются качественно эквивалентными, если существует не-
прерывное взаимно однозначное преобразование, которое перево-
дит фазовый портрет одной системы в фазовый портрет другой,
так что сохраняется ориентация траектории (тип фазового портрета).
x |
|
|
|
x2 |
2 |
e |
2 |
||
|
|
|
|
ˆ
T
x |
x1 |
|
1 |
|
|
|
|
|
|
x 2 |
x 2 |
e |
1 |
x1 x2 |
C |
C |
|
||||
1 |
2 |
|
|
|
|
Рис. 3.1. Сохранение фазового портрета «седло» при переходе к новой системе координат
ПРИМЕР 3.4. Линейному дифференциальному уравнению вто-
