Матика 2 курс / Дифференциальные уравнения 2б

111

ектория - замкнутая линия вокруг центра. Когда энергия достигает критического значения Е = 0 частица движется по особой траекто-

рии - сепаратрисе (смысл этого названия будет прояснен ниже).

Наконец, когда энергия Е становится больше нуля, частица способ-

на преодолеть барьер, разделяющий ямы потенциала, и траектория становится замкнутой линией, обходящей все три положения рав-

новесия системы (рис. 4.6). Теперь становится понятным смысл названия критической траектории Е = 0 «сепаратриса». Эта траек-

тория разделяет траектории на два качественно различных вида -

локализованные (около конкретного центра) и делокализованные

(обходящие оба центра и седло).

Особенностью рассматриваемой системы является возмож-

ность точно проинтегрировать уравнение сепаратрисы:

и получить его решение в виде

Сепаратриса начинается вблизи седла при τ = - ∞ и вновь при-

ближается к седлу при τ = + ∞, проходя точку максимального уда-

ления от седла при τ = 0 . Особенность сепаратрисы заключается в следующем. Если для обхода любой из замкнутых траекторий (рис.

4.6) требуется конечное время, то для обхода по сепаратрисе - бес-

конечное время (в силу теоремы единственности, фазовые траекто-

рии не пересекаются).

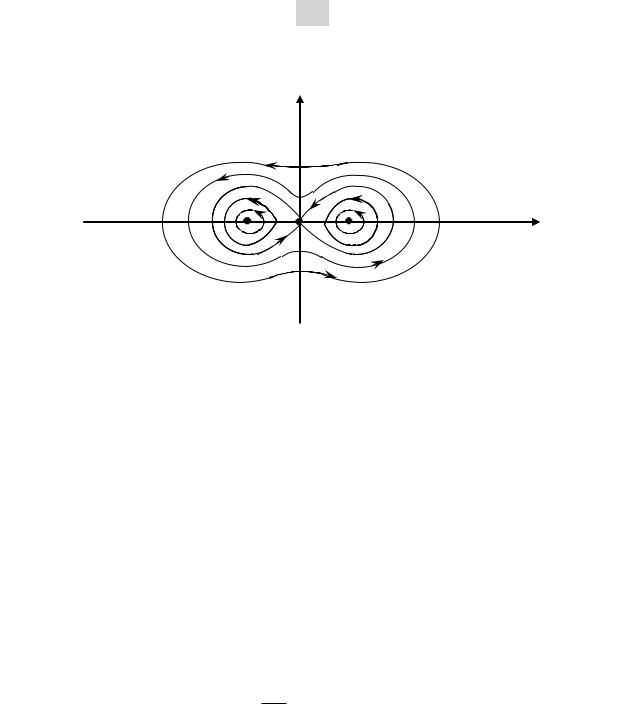
112

q

Рис. 4.6. Фазовые траектории в отсутствии затухания и вынуж-

дающей силы

ЗАДАЧА 4.8. Проинтегрируйте (4.19), используя замену u = 1/q.

Рассмотрим изменение фазовых траекторий при включении слабого затухания 0 < γ << 1 . В этом случае система уравнений имеет вид

dqdt p ,

Его положения равновесия расположены там же, где и у системы без затухания, однако их характер изменяется: р = q = 0 по-

прежнему седло; р = 0, q = ± 1 - устойчивые фокусы.

ЗАДАЧА 4.9. Исследуйте тип положений равновесия (4.21).

В присутствии затухания энергия убывает, поскольку в силу

113

уравнения (4.21)

dHdt p dpdt (q3 q) dqdt p2 0.

Отсутствие сохранения энергии приводит к разрушению за-

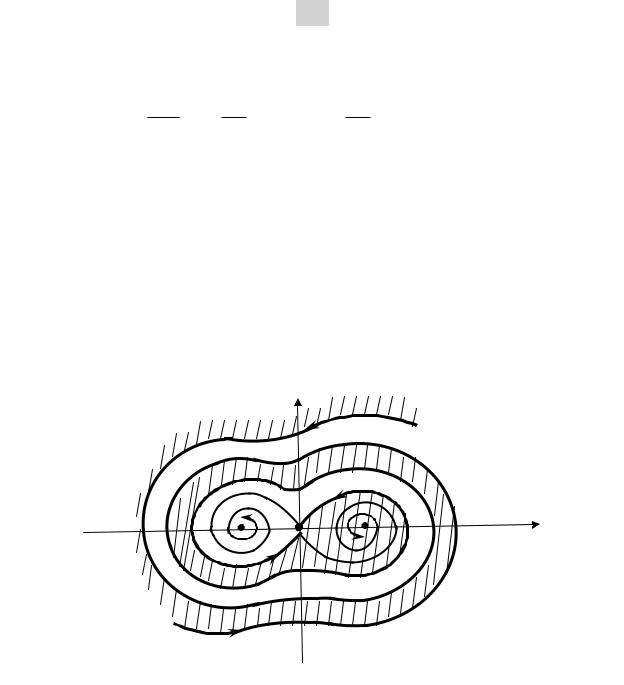
мкнутости сепаратрисы и разбиению фазового пространства вдали от фокусов на систему двух чередующихся качественно различных слоев: система «притягивается» к определенному фокусу только в том случае, если она находится во вполне определенном слое фазо-

вого пространства (рис. 4.7).

q

Рис. 4.7. Разбиение фазового пространства на слои в присутствии затухания незамкнутыми сепаратрисами

Исследуем, как изменяется характер фазовых траекторий в от-

сутствии затухания при действии на систему слабой 0 < f << 1 вы-

нуждающей силы частоты ω. Уравнения движения имеют вид

114

dqdt p ,

Будем искать поправки, обусловленные внешней силой, к не-

возмущенной траектории (4.18) (q0 (τ), p0 (τ)) . Представляя исход-

ное решение в виде

и, выполняя линеаризацию в (4.22), получаем

Это уравнение описывает вынужденные колебания линейной системы с переменной частотой. В отсутствии резонанса исходная фазовая траектория получает, согласно (4.23), приращение, про-

порциональное амплитуде вынуждающей силы. Если исходная тра-

ектория замкнутая, за один период невозмущенных колебаний воз-

мущенная траектория пересекает возмущенную конечное число раз.

Если невозмущенная траектория - сепаратриса, то соответ-

ствующая ей возмущенная траектория пересечет сепаратрису бес-

конечное число раз. Это связано с тем фактом, что обход по сепара-

115

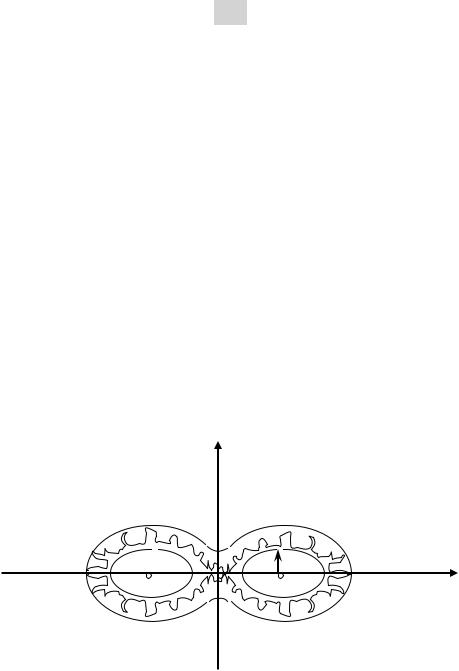
трисе требует бесконечного времени. Следовательно, вынуждаю-

щая сила превращает сепаратрису исходной системы из гладкой кривой в «дрожащую», с амплитудой пропорциональности f (рис.

4.8).

Рассмотрим качественную картину возникновения хаотиче-

ского режима при совместном действии вынуждающей силы и за-

тухания. Под воздействием вынуждающей силы сепаратрисы си-

стемы с затуханием (рис. 4.7), разделяющие фазовое про-

странство на слои, ведущие к различным фокусам, начинают

«дрожать».

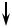~ f

q

Рис. 4.8. Сепаратриса возмущенная вынуждающей силой f cos

Увеличение затухания γ «раздвигает» сепаратрисы, а возрас-

тание амплитуды силы f усиливает их «дрожание». Если удается установить, что сепаратрисы имеют точку пересечения, это будет означать, что они пересекаются бесконечное число раз. Следова-

тельно, необходимо иметь некоторый критерий пересечения сепа-

117

описывает убывание энергии за счет затухания, второе - ее измене-

ние за счет действия вынуждающей силы. Знак второго слагаемого чувствителен к начальной фазе ωτ0. Знак H ( 0 ) отрицательный,

если

и является неопределенным в противоположном случае. Именно условие неопределенности знака H ( 0 ) и служит критерием хао-

тического режима:

Как показывает сравнение критерия (4.26) с результатами фи-

зических и численных экспериментов, он дает нижнюю границу области хаотических режимов. Таким образом, критерий хаоса

(4.26) следует понимать в следующей трактовке.

Если параметры системы γ, f, ω не удовлетворяют критерию

(4.26), движение системы строго предсказуемо.

Если γ, f, ω удовлетворяют (4.26), возможно возникновение хаотического режима, при котором движение системы становится непредсказуемым.

118

ПРИЛОЖЕНИЕ 1.

НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ЛИНЕЙНОЙ АЛГЕБРЫ

Наиболее важными примерами линейных пространств могут

служить множество векторов размерности n : Rn ; множество мат-

риц порядка n : an ; множество функций, непрерывных на от-

резке. Для любых элементов этих множеств определены линейные операции - умножение на число и сложение.

Базисом в линейном пространстве Rn называют упорядочен-

ную систему линейно независимых векторов (элементов простран-

ностью пространства. Любой элемент пространства (вектор) может быть выражен через элементы базиса единственным образом:

базисе. При этом вектор задается своими координатами, например,

в виде матрицы-столбца:

x1x2

X... .

....

xn

Впространстве Rn определено бесконечное количество бази-

119