Матика 2 курс / Дифференциальные уравнения 2б

103

в точках локальных экстремумов (-1, 2ε / 3), (1, - 2ε / 3) происхо-

дит «срыв» - смена знака амплитуды ~ . Поэтому движение осцил- q

лятора Ван дер Поля с сильной нелинейностью можно приближен-

но представить в виде, изображенном на рис. 4.2 б.

Большому изменению ~ соответствует изменение амплитуды p

вой точки ~ ~ по линии (4.11) (участки АВ и СD на рис.

(q( ), p( ))

Переходя от координат ( ~ ~ ) к исходным фазовым координа- q, p

там (q, р), переходим к представлению предельного цикла в виде,

приведенном на рис. 4.3.

ЗАДАЧА 4.4. Исходя из формул (4.9), (4.11) и рис. 4.2, полу-

чите рис. 4.3.

(dp / d 0) значения импульса.

104

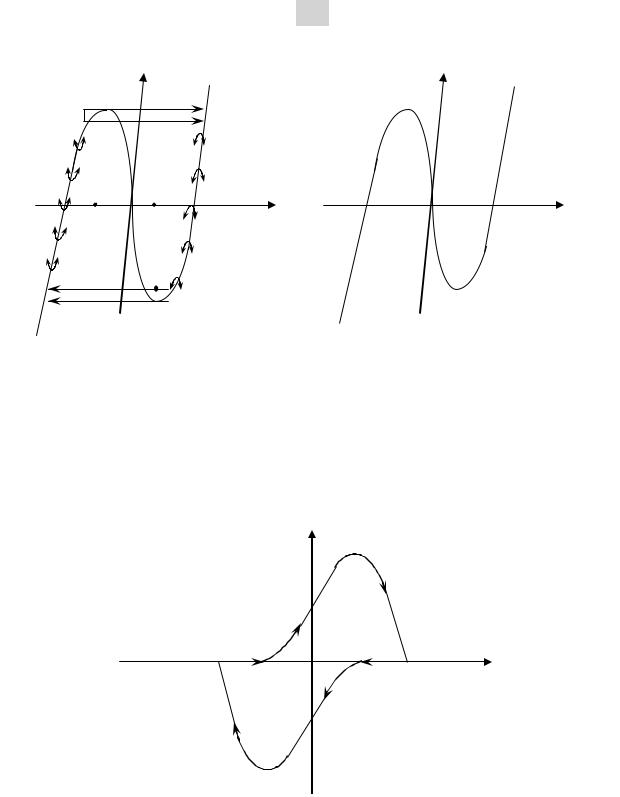
Рис. 4.2. Качественный портрет (а) и приближенный предельный цикл (б) осциллятора Ван дер Поля на плоскости Льенара в случае сильной нелинейности

Рис. 4.3. Предельный цикл осциллятора Ван дер Поля на фазовой плоскости в случае сильной нелинейности

Найдем приближенно явный вид зависимостей q (τ) и период колебаний в случае сильной нелинейности, используя вид фазовой

106

q

2

1

1

2

Рис. 4.4. Релаксационные колебания осциллятора Ван дер Поля.

ЗАДАЧА 4.5. Получите формулу (4.13).

Поскольку, из условий сшивки следует

для полупериода получаем:

Следовательно и в случае сильной нелинейности ε >> 1 осциллятор

обратно пропорциональной ε. Этот режим называется релаксацион-

ными колебаниями.

107

Таким образом можно сделать вывод, что существование ав-

токолебательного режима является универсальным свойством ос-

циллятора Ван дер Поля в случае любой нелинейности 0 < ε < +∞,

а от конкретного значения параметра ε = γ / ω зависит, в частности,

частота, автоколебаний, тогда как амплитуда остается практически постоянной.

108

4.2.ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

ВСИММЕТРИЧНОМ ДВУХЪЯМНОМ ПОТЕНЦИАЛЕ ПРИ НАЛИЧИИ ЗАТУХАНИЯ

Затухающие колебания частицы в двухьямном потенциале

(рис. 4.5) под действием гармонической силы являются примером системы, обладающей хаотическим поведением.

После перехода к соответствующим безразмерным перемен-

ным уравнение, описывающее процесс, может быть записано в ви-

де:

U

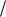14

Рис. 4.5. Симметричный двухъямный потенциал u(q) q4 / 4 q2 / 2

Вводя новые переменные p dq / dt и z , перепишем

(4.14) в виде автономной системы третьего порядка

109

Тот факт, что фактический порядок уравнения (4.14) п = 3, не явля-

ется случайным. Как показали многочисленные исследования (см.

например, [5]), п = 3 является низшей размерностью автономных систем, обладающих хаотическим режимом.

Исследование решений (4.15) начнем с простейшей ситуации

f = γ = 0 (отсутствие затухания и вынуждающей силы). Тогда уравнение

dqdt p,

и, следовательно, его фазовые траектории - линии уровня постоян-

ной энергии Н (q, р) = E.

ЗАДАЧА 4.6. Получите формулу (4.17).

Поскольку p dq / dt dq / d при фиксированном E получаем параметрическое уравнение траектории при помощи интегрирова-

ния уравнения с разделяющимися переменными:

Или после разделения переменных

Входящий в (4.18) интеграл не вычисляется через элементарные функции при произвольном Е. Он называется эллиптическим инте-

гралом, и связанные с ним функции q (τ) - эллиптическими функци-

ями (теория эллиптических функций достаточно сложна и здесь не рассматривается).

Качественный анализ фазовых траекторий (4.18) в зависимо-

сти от E проведем на основе линейного приближения для (4.16) и

интеграла энергии (4.17).

Уравнение (4.16) имеет три положения равновесия р = q = 0

и p = 0, q = ± 1 . Положение равновесия р = q = 0 - седло, два

других положения равновесия: p = 0, q = ± 1- центры.

ЗАДАЧА 4.7. Проведите классификацию положений равнове-

сия уравнения (4.16).

Поскольку потенциал имеет два минимума u ( 1) 1/ 4 , a

p2 0 , из вида интеграла энергии следует, что фазовые траекто-

рии не существуют при Е 1/ 4, а при E 1/ 4 фазовые траекто-

рии - положения равновесия q1 1, q2 1. Если 1/ 4 E 0

частица заперта около того положения равновесия, q1 1 или q2 1, около которого она находилась в начале и ее фазовая тра-