
Матика 2 курс / Дифференциальные уравнения 2б
.pdf
11
ПРИМЕР 1.2. Проанализировать решение линейного уравнения
первого порядка:
dX |
kX b, |
k 0 . |
(1.3) |
|
dt |
||||
|
|
|
Уравнение имеет одно положение равновесия Xeq = - b / k , а
поле направлений дифференцируемо. Вводя новую функцию, укло-
нение от равновесия U (t) X (t) - X eq , перейдем от исходного урав-
нения к уравнению для U t :
dU |
kU, |
Ueq 0. |
(1.4) |
|
d t |
||||
|
|
|
Фазовые пространства для уравнений (1.3) и (1.4) различают-
ся только положением состояния равновесия на фазовой оси.
При U > 0 ( X X eq - b / k) состояние удаляется от положения
равновесия. При U < 0 ( X X eq ) состояние также удаляется от равновесного.
Фазовые траектории системы – лучи X0 , , или |
, X 0 , |
или точка X 0 b / k . |
|
Преобразование координат (t,X) = (t,U - kt) (t,(X - Xeq )e- kt) пе-
реводит интегральные кривые в прямые, параллельные оси Ot, то
есть осуществляет выпрямление поля скоростей:
dY |
|
d (Ue k t ) |
|
dU |
|
- kt |
- kt |
0, |
|
|
|
e |
|
- Uke |
|||
dt |
dt |
dt |
|
|||||
|
|
|
|
|
|
что показано на рис. 1.2.
12
U |
U |
y |
V |
t |
t |
|
||
|
|
a) |
á) |
â) |
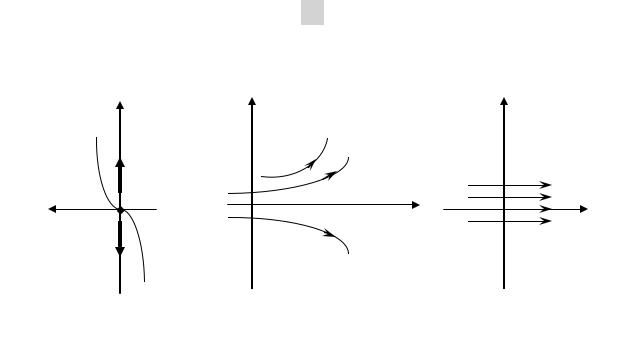
Рис.1.2. Фазовые траектории (а), интегральные кривые (б) и
выпрямленные интегральные кривые (в) линейного уравнения (1.3),
(1.4)
Заметим, что выпрямляющее преобразование удалось постро-
ить при помощи известного решения (1.4) U e kt |
(в чем легко |
1 |
|
убедиться прямой подстановкой). Следовательно, любое решение
U (t) может быть получено из U = ekt умножением на константу |
|||||
|
|
|
|
1 |
|
Y |
U(a) - начальное значение в момент времени t = 0. U (t) Y e kt |
||||
0 |
|
|
|
|
0 |
Y |
U (t)e kt const - прямая, |
параллельная оси |
Ot на плоскости |
||
0 |
|
|
|
|
|
t,Y . |
|
|
|||
|
ПРИМЕР 1.3. Показать, что для уравнения |
|
|||
|
|
dX |
|
3 (X-a) 2/ 3, a 0 |
(1.5) |
|
|
dt |
|||
|
|
|
|
||
нарушается условие единственности решения (непересечения фазо-
вых траекторий и интегральных кривых).
13
Положение равновесия X = a - решение уравнения (1.5). Урав-
нение для уклонения U X a |
имеет вид: |
|
||
|
dU |
3 U 2 / 3 |
. |
(1.6) |
|
d t |
|||
|
|
|
|
|
Прямой подстановкой убеждаемся, что U (t) (t - t0 ) 3 - решение уравнения (1.6). Следовательно,
X (t) a (t -t ) 3 |
(1.7) |
0 |
|
решение (1.5). Фазовая скорость всегда положительна. Кривая
(1.7) пересекает прямую X a , если начальное значение
X (t0 ) X 0 a.
x |
x |
x a
x0
V |
t |
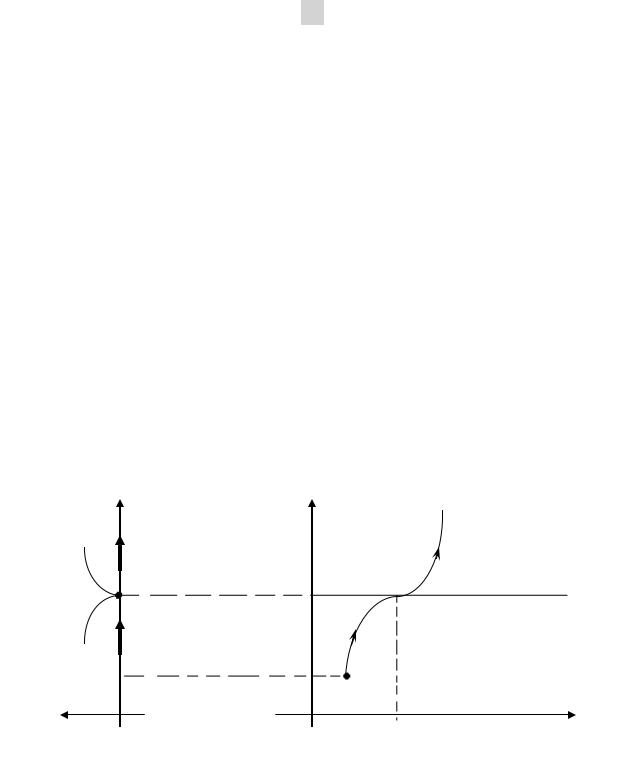
Рис. 1.3. Нарушение единственности решения уравнения (1.5):
фазовая траекториялуч [x0 , ) пересекает положение равновесия
x a , x0 a
Следовательно, единственность решения нарушается за счет пересечения фазовой траектории с положением равновесия (рис. 1.3). При этом нарушение единственности происходит именно в той
14
точке фазового пространства X = a, где поле направлений не явля-
ется гладким (производная d(X-a)2/ 3 2/ 3(X-a) -1/ 3 не существует dX
при X = a). Это полностью согласуется с основной теоремой о вы-
прямлении.
В приведенных примерах встречались различные состояния равновесия: к одним состояние системы приближалось в процессе эволюции, от других удалялось.
Дадим классификацию состояний равновесия системы -
решений уравнения V(x) = 0, где V(x) - гладкая функция в состоянии
равновесия (рис. 1.4).
x |
x |
x |
x |
V |
V |
|
V |
V |
|
а) |
б) |
в) |
г) |
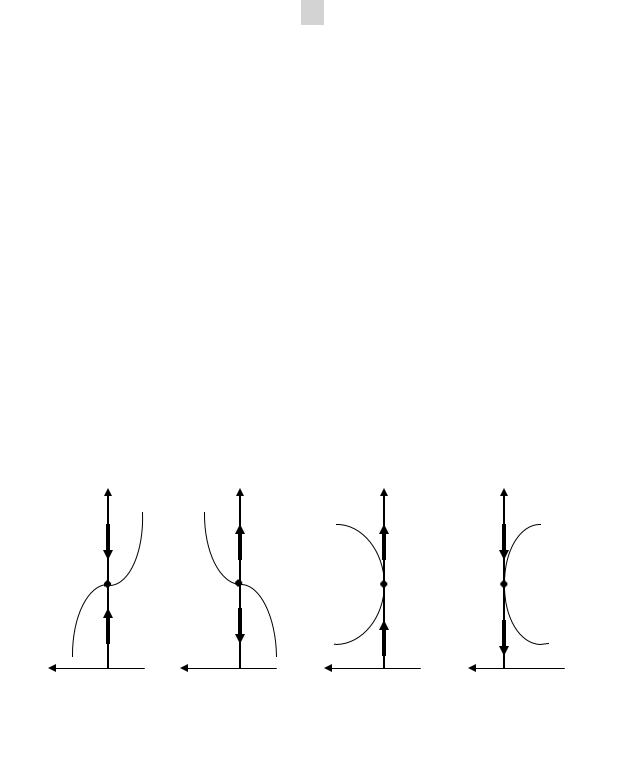
Рис 1.4. Аттрактор (а) и неустойчивые положения равновесия:
репеллер (б), шунты (в, г)
ОПРЕДЕЛЕНИЕ 1.1.
Состояние равновесия X = a, V(a) = 0 называется устойчивым или аттрактором (притягивающим), если в его окрестности фазо-
вая скорость направлена по направлению к состоянию равновесия.

15
ОПРЕДЕЛЕНИЕ 1.2.
Состояние равновесия X = a, V(a) = 0 называется неустойчи-
вым, если фазовая скорость в его окрестности направлена от состо-
яния равновесия (репеллер), либо не меняет знак при переходе через состояние равновесия (шунт).
Если два уравнения имеют одно положение равновесия, то тип их положений равновесия может либо различаться, либо совпадать.
ОПРЕДЕЛЕНИЕ 1.3.
Два различных уравнения вида (1.1) с одним положением рав-
новесия называются качественно эквивалентными, если их по-
ложения равновесия однотипны.
ПРИМЕР 1.4. Исследовать на качественную эквивалентность
уравнения: |
|
|
|
|
|
|
|
|
а) |
dX |
X ; |
б) |
dX |
sh (X - a); |
в) |
dX |
(X-b)2 . |
dt |
dt |
|
||||||
d t |
Все уравнения имеют по одной неподвижной точке и их поля направлений - гладкие. Фазовые портреты (схемы фазовых траек-
торий) приведены на рис. 1.5.
Уравнения (а) и (б) имеют однотипные положения равновесия
- репеллеры (отталкивающие) и, следовательно, качественно экви-
валентны.
Если система имеет несколько положений равновесия, то для разбиения уравнений на качественно эквивалентные классы стано-
вится важным не только число положений равновесия и их тип, но и последовательность их чередования.
16
x |
x |
x |
|
a |
b |
|
0 |
|
V |
V |
V |
|
|
|
а) |
б) |
в) |
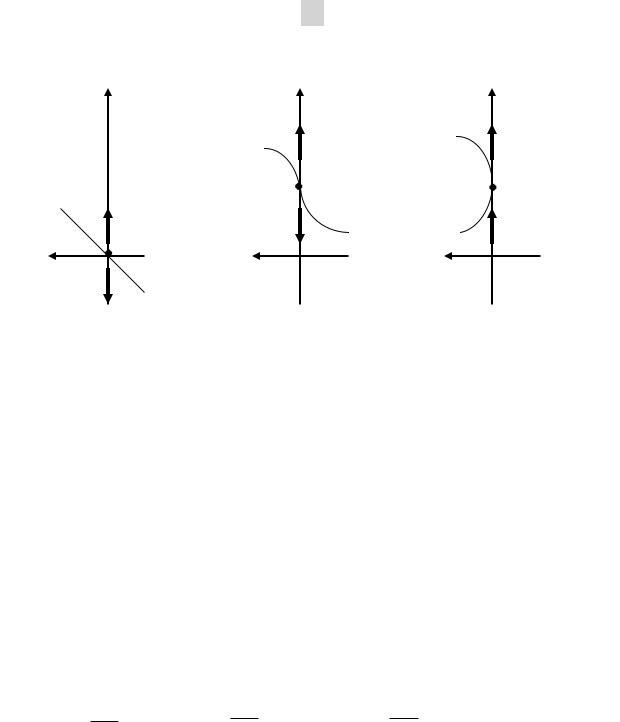
Рис. 1.5. Фазовые портреты к примеру 1.4
ОПРЕДЕЛЕНИЕ 1.4.
Два уравнения вида (1.1) называются качественно эквивалент-
ными, если они имеют равное число положений равновесия, упоря-
доченных по возрастанию и характер положений равновесия с оди-
наковыми номерами, совпадает.
ПРИМЕР 1.5. Какие из уравнений качественно эквивалентны:
а) dXdt X 2 -1; б) dXdt X (X -1); в) dXdt (X 2)( X 1) .
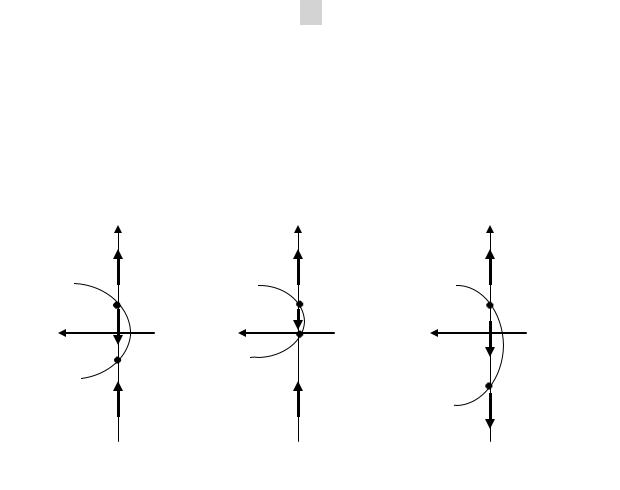
Все уравнения имеют по две неподвижные точки. Фазовые портреты приведены на рис. 1.6.
Из фазовых портретов видно, что все три уравнения имеют нижнее (меньшее) положение равновесия - аттрактор, и верхнее -
репеллер. Следовательно, все три уравнения качественно эквива-
лентны.
17
В некоторых случаях уравнения вида (1.1) могут быть решены аналитически. Это решение сводится к вычислению некоторого ин-
теграла и формулируется следующей теоремой.
x |
x |
x |
1
V
1
|
1 |
1 |
V |
0 |
V |
2
Рис. 1.6. Фазовые портреты к примеру 1.5
ТЕОРЕМА БАРРОУ. Если Х0 не является положением рав-
новесия дифференциального уравнения dX / dt = V(X) с гладким по-
лем направлений, то его решение X(t) с начальным условием
X (t0 ) X 0 дается формулой:
t t0 |
X (t ) |
dx |
, |
(1.8) |
|||
|
|
|
|||||
V (x) |
|||||||
|
X |
0 |
|
|
|||
|
|
|
|
|
|
||
определяющей решение X(t) в неявном виде.
Из (1.8) видно, что успех аналитического решения зависит от возможности вычисления входящего в (1.8) интеграла, а это, как хорошо известно, возможно не всегда.
ПРИМЕР 1.6. Найти аналитически решение уравнений

18
а) |
dX |
kX ; |
б) |
dX |
X 2 -1. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно (1.8) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
t - t |
0 |
1 |
|
X |
dx |
|
|
|
1 |
ln | x |
|
X |
; |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(а) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
k |
|
X |
|
|
x |
|
|
|
|
k |
|
|
|
|
|
X |
0 |
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X |
|
dx |
|
|
|
|
1 |
|
|
|
x 1 |
|
|
X |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
t - t0 |
|
|
|
|
ln |
|
|
|
|
|
|
|
(б) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
X0 x2 1 |
|
|
2 |
|
x 1 |
|
|
X0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Если X0 ≠ 0 в случае «а», и X0 ≠ ± 1 в случае «б», освободив- |
|||||||||||||||||||||||||||
шись от логарифмов, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
X X0 e |
k(t-t0 ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
(а) |
|||||||||
X |
|
( X 0 1) |
|
|
|
|
( X 0 1)e |
2(t t |
0 ) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
( X 0 1) |
|
|
|
|
( X 0 |
1)e |
2(t t |
0 |
) . |
|
(б) |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Важно, что приведенные формулы дают правильные решения и в том случае, когда начальное условие является положением рав-
новесия:
X (t) |X |
0 , |
(а) |
|
0 |
|
X (t) |
|
1; |
X (t) |
|
1. |
(б) |
|
X |
1 |
|
X |
1 |
|
|
|
0 |
|
|
0 |
|
ЗАМЕЧАНИЕ. Наше внимание не случайно было направлено на автономные уравнения (1.1), так как к ним сводятся многие не-
автономные уравнения:
|
19 |
|
|
|
dX |
V (X ,t), |
(1.9) |
||
|
||||
dt |
|
|||
допускающие аналитическое решение.
Когда поле направлений
V (X ,t) F(X ) G(t),
уравнение (1.9) называется уравнением с разделяющимися пере-
менными:
dX |
F(X )G(t). |
(1.10) |
|
||
dt |
|
|
Его решение с начальным условием X(t0) = X0 дается формулой ти-
па (1.8):
X |
dx |
t |
G(t) dt . |
(1.11) |
|
∫F(x) |
|||||
∫ |
|
||||
X 0 |
|
t0 |
|
|
|
Из (1.11) видно, что введение вместо t нового «времени»
T G(t)dt
сводит уравнение (1.10) к автономному уравнению.
Если поле направлений имеет вид:
V (X ,t) h X / t ,
то неавтономное уравнение
dX |
h(X /t) |
(1.12) |
|
||
dt |
|
|
называется однородным. Замена искомой функции X (t) через вспомогательную U (t) = X / t сводит (1.12) к уравнению с разделя-
ющимися переменными:
dX |
U t |
dU |
; |
dU |
|
h(U ) U |
. |
(1.13) |
|
|
|
|
|||||
dt |
|
dt |
|
dt |
|
t |
|
|

20
Следовательно, и однородное неавтономное уравнение (1.12)
сводится преобразованием переменных к анализу автономного уравнения.
Аналогично, при помощи последовательных преобразований переменных, решается и неоднородное линейное (содержащее ис-
комую функцию и ее производную в первой степени) уравнение с
переменными коэффициентами:
dX |
a(t)X b(t). |
(1.14) |
|
||
dt |
|
|
Решение (1.14) разбивается на два этапа. Сначала находим решение однородного линейного уравнения с разделяющимися пе-
ременными:
|
|
|
dX |
a (t) X ; |
|
|
|
|
|
|
|
|
(1.15) |
||
|
|
|
d t |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
t |
|
|
|
X |
f |
(t) exp ( |
a(t)dt) |
. |
(1.16) |
||
|
|
|
∫ |
||||
|
|
|
|
t0 |
|
|
|
Далее решение (1.14) находим в виде суммы: |
|
||||||
|
|
X (t) CX f |
(t) X f (t)A(t) , |
(1.17) |
|||
где константа С определяется из начального условия X (t0) = X0 и
равна C = X0 при условии, что так называемое частное решение
X1(t) A t X f (t), |
(1.18) |
удовлетворяет уравнению (1.14) и начальному условию X1 (t0) = 0.
Подстановка (1.18) в (1.14) дает уравнение для A(t):
