Матика 2 курс / Дифференциальные уравнения 2б

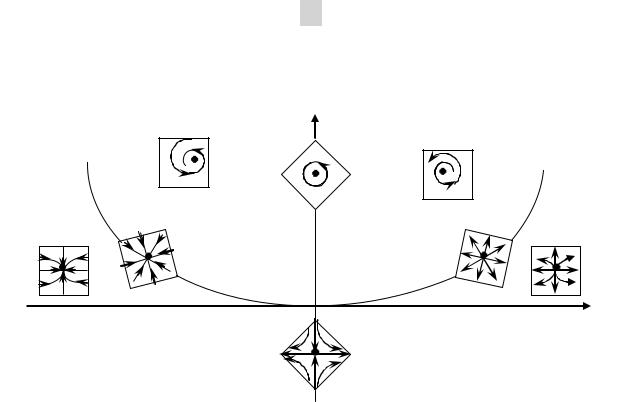
61

det A

Sp A

Рис. 3.12. Зависимость характера фазового портрета от свойств матрицы А

2). Из проведенных исследований следует, что линейные преобразования сохраняют качественное поведение решений и лю-

бая линейная система на плоскости, имеющая одну неподвижную точку, качественно эквивалентна одной из систем, фазовыми порт-

ретами которых являются: узел (устойчивый или неустойчивый);

вырожденный узел (устойчивый или неустойчивый); седло, фокус

(устойчивый или неустойчивый), центр. Тип фазового портрета определяется корнями характеристического уравнения матрицы си-

стемы А, которые в свою очередь определяются через Det А и Sp А.

Это позволяет определить тип фазового портрета и характер устой-

чивости точки (0,0) непосредственно по значению Sp А и Det А по диаграмме (рис. 3.12). Все фазовые портреты, соответствующие устойчивому положению равновесия точки (0, 0) находятся во вто-

62

ром квадранте: Sp A < 0; Det A > 0.

ЗАДАЧА 3.1. Запишите общее решение однородных уравне-

ний по таблице 3.1

а) d 2 x / dt 2 5dx / dt 6x 0 б) d 2 x / dt 2 2dx / dt x 0

в) d 2x / dt 2 6dx / dt 13x 0

ЗАДАЧА 3.2. Перепишите уравнение колебаний

d 2 x / dt 2 2 dx / dt 02 x 0

в виде эквивалентной ему системы. Запишите характеристическое уравнение и проанализируйте характер изменения фазового порт-

рета при изменении коэффициента трения γ:

ПРИМЕЧАНИЕ. Если Det А = 0, то хотя бы одно из собственных значений 0. Тогда линейная система называется непростой. От-

сюда следует, что существует ненулевые решения системы

a11x1 a12x2 0 a21x1 a22x2 0,

и кроме начала координат система имеет другие неподвижные точ-

ки. Существует две возможности а) А = 0 (все точки неподвижны)

б) ранг матрицы А равен 1 (неподвижные точки образуют прямую проходящую через начало координат).

63

ПРИМЕР 3.6. Система

dx1 4x1 2x2 dt

dx2 2x1 x2 dt

находим уравнение фазовых траекторий:

x2 x1/ 2 C.

x2

x1

Рис. 3.13. Фазовый портрет системы 3.6, имеющей множество неподвижных точек

64

3.4. АЛГОРИТМ РЕШЕНИЯ ОДНОРОДНОЙ СИСТЕМЫ

Запись решения линейной однородной системы в матричной

форме удобно выполнить, используя матрицу e A t , которая называ-

ется матричной экспонентой:

мой подстановкой e A t в систему

убеждаемся, что X e At - решение.

x (t)

Обозначив X 1 - матрицу искомых функций, а

x2 (t)

решение системы (3.26) в компактном виде

X e A(t t0 ) X 0

65

ЗАМЕЧАНИЕ 1. Вид матрицы eJt легко получается непосред-

ственной подстановкой в формулу

найдена по формулам

а) для случая различных собственных значений (действитель-

б) для случая одинаковых собственных значений 1 2 0

eAt e 0t E t A 0 E ,

1 0 где E .

0 1

66

Таблица 3.2. Определение вида матрицы e J t

Исходя из вышеизложенного, алгоритм нахождения решения можно разделить на несколько шагов. Рассмотрим это на примере.

ПРИМЕР 3.7. Найти решение системы

Найдем след и определитель матрицы системы

Согласно рис. 3.12 отрицательное значение определителя Det A < 0

свидетельствует о том, что неподвижная точка x1 x2 0 является неустойчивым положением равновесия, а фазовый портрет является

«седлом».

Шаг 2. Запишем характеристическое уравнение матрицы А и

найдем собственные значения матрицы А

Шаг 3. По виду собственных значений 1, 2 согласно табл. 3.2 или приложения П. 1.9 выбираем матрицу

Приравнивая элементы матрицы, стоящие на одинаковых местах,

получаем систему уравнений:

которая имеет множество решений, удовлетворяющих соотноше-

ниям

a c

2b d .

Выбирая простейшее из этих решений, получаем матрицу перехода

Шаг 7. По виду матрицы J выберем матрицу eJt по табл. 3.2.

и находим матрицу e A t :

Эта запись удобна тем, что позволяет сразу находить решение

ЗАДАЧА 3.3. Решите системы уравнений:

3.5. НЕОДНОРОДНЫЕ СИСТЕМЫ

Неоднородные линейные системы дифференциальных урав-

нений с постоянными коэффициентами имеют вид