Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Матика 2 курс / Дифференциальные уравнения 2б

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

2.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

рого порядка

d	2x			dx
		2	3	2	2x	2	0
		2
dt				dt

соответствует система уравнений

dxdt1 3x1 2x2

dx2 x1 dt

с матрицей коэффициентов		3	2
с матрицей коэффициентов	A			.
		1	0
		1	0

Исключив параметр t из системы уравнений, для нахождения фазовых траекторий получаем однородное дифференциальное уравнение

		dx1		3 2				x2		.
				3 2						.
		dx2							x1
Обозначив x / x					2	,	dx / dx					d / dx		x	, по-
	1				2				1		2		2	2
лучаем
	ln cx		ln( 1)/( 2)2 .												(3.5а)
	2
При c 1 имеем семейство парабол
x 2	4x x				4x 2				x		x	2	0		(3.6)
1	1		2				2		1			2

с осью симметрии, расположенной под углом 1/ 2arctg(4 / 3) к

оси ОХ1.

Замечание.	Тип кривой определяется из общего уравнения
кривой второго	порядка	Ax 2	2Bx x	2	Cx	2 Dx Ex		F 0.
		1	1	2	2	1	2

										42
Параболическому типу соответствует АС В2 0 ;																				эллиптическому
типу AC B2 0;						гиперболическому типу AC B2														0.
	Для приведения системы к более простому виду находим соб-
ственные значения матрицы А: 1 2;																2	1 и собственные векто-

		2	,			1
ры:	e		,	e
ры:	1			2		.
		1			1

	Матрица перехода от базиса											E		i , j			к базису			E						имеет
	Матрица перехода от базиса											E		i , j			к базису			E	2	e		, e	2	имеет
												1									2		1		2
вид
							2	1									1	1
					T		1					T	1				1
							1	1	;								1	2

	В базисе Е2 исходная матрица принимает простой вид
											2			0		:
								J								:
											0			1
											0			1
								1	1			3		2			2	1	2		0
			J T
			J T		1AT
								1				1			0				0 1				,
								1	2			1			0		1 1		0 1

а исходная система преобразуется в систему

dxdt1 2x1 dxdt2 x2.

После исключения t и интегрирования получаем уравнения фазовых траекторий, которые также являются параболами

x22 cx1 .

Построение фазовых траекторий (3.6) вызывает затруднения.

Поэтому для построения фазовых траекторий в случае «седла» и

«вырожденного узла» нужно, прежде всего, найти фазовые траек-

тории, которые лежат на прямых, проходящих через начало коор-

динат. Эти направляющие прямые - сепаратрисы всегда направле-

ны вдоль собственных векторов матрицы А. Для особой точки типа

«узел» траектории касаются той прямой, которая направлена вдоль собственного вектора, соответствующего меньшему по абсолютной величине значению (рис 3.2).

Уравнения направляющих прямых можно найти из уравнения

(3.5), положив x2 = kx1 ,

dx1 3 2 x2 dx2 x1

3 2k;

2k 2 3k 1 0;

k 1;

;

x x ;

x1.

( 1 )

e1 ( 2 )

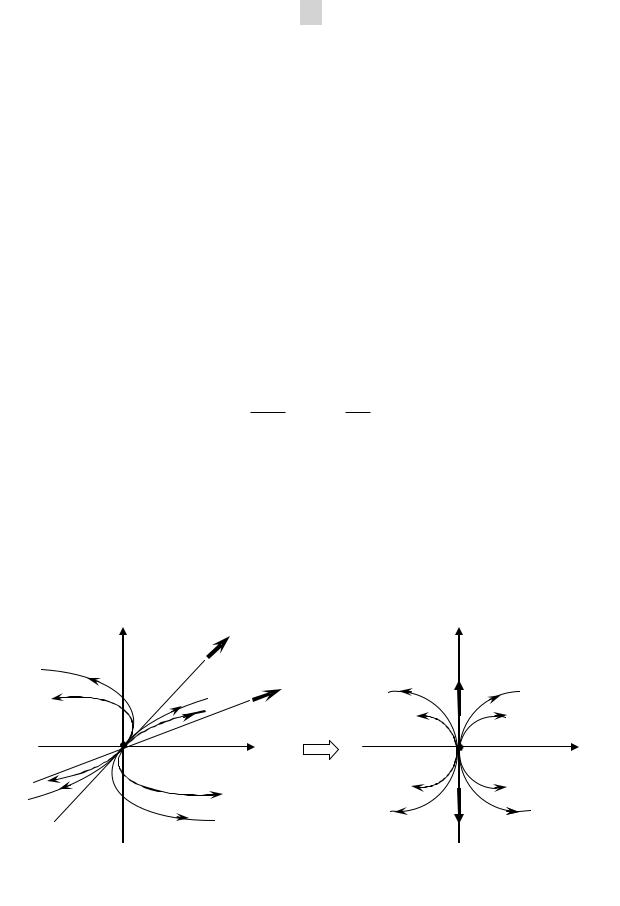
Рис.3.2.Сохранение характера фазового портрета типа «неустой-

чивый узел» при переходе к новой системе координат (пример 3.4)

ПРИМЕР 3.5. Дифференциальному линейному уравнению

d	2x			dx
		2	2	2	x	2	0
		2	2		x		0
dt				dt
				dt

соответствует система

dxdt1 2x1 x2 dxdt2 x1

с матрицей коэффициентов

	2	1	,
A			,
	1	0
	1	0

которая имеет два одинаковых собственных значения λ0 = 1. Урав-

нения фазовых траекторий имеют вид

dx1 2 x2 , dx2 x1

а фазовые траектории задаются семейством кривых x2 (x1 x2 ) ln( x1 x2 )c.

		1	2	переводит матрицу А к матрице J вида
Матрица T				переводит матрицу А к матрице J вида
			1
		1	1

J	1	1
J		.
	0
	0	1

			1			2
В новом базисе					e		система дифференциаль-
В новом базисе	e			,	e		система дифференциаль-
		1	1		2	1

ных уравнений имеет вид

	dx1		x	x
			x	x
	dt	1		2
	dt
	dx2		x ,
			x ,
	dt	2
	dt

а фазовые траектории задаются уравнением					x1 x2 ln	Cx2

(рис. 3.3).

x	2	x	2
	2

	ˆ
	T
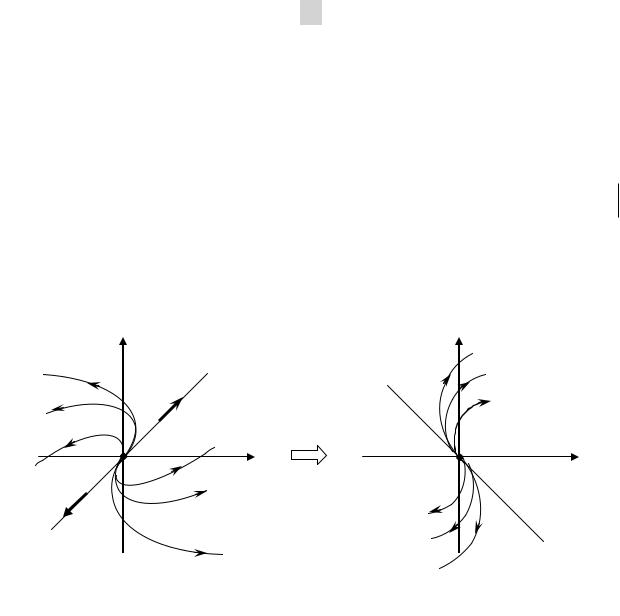
x1	x1

Рис.3.3. Сохранение характера фазового портрета «неустойчивый вырожденный узел» при переходе к новой системе координат в примере 3.5.

Обобщая примеры 3.3, 3.4, 3.5 видим, что любую линейную систему уравнений (матрицу системы) можно привести к простей-

шему (каноническому или жорданову) виду. Качественное поведе-

ние решения (характер фазового портрета) при этом сохраняется и определяется собственными значениями матрицы А, которые не изменяются при преобразованиях подобия (выборе новой системы координат).

Системы линейных дифференциальных уравнений, которые имеют один и тот же характер фазового портрета, называют качественно эквивалентными.

Следовательно, для решения линейных дифференциальных уравнений второго порядка необходимо:

1- расклассифицировать все линейные системы второго по-

рядка по характеру собственных значений;

2 - исследовать все простейшие качественно различные типы линейных систем;

3 - построить алгоритмы решения исходной системы на осно-

ве известного решения качественно эквивалентной ей простейшей системы.

3.3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННО РАЗЛИЧНЫХ

ТИПОВ ЛИНЕЙНЫХ СИСТЕМ

Классы эквивалентности для матриц второго порядка опреде-

ляются собственными значениями матрицы А (корнями характери-

стического уравнения):

a11	a12	0

a21	a22

	SpA	(SpA)2 4DetA

1,2		2
		2

	47
SpA a11 a22;	DetA a11a22 a12a21

(подробнее см. Приложение I). При этом возможны следующие случаи.

СЛУЧАЙ 1. Собственные значения матрицы А действитель-

ные и различные 1 2 .

Матрица системы А может быть приведена к простейшему ви-

ду

		0
	1
J	0		.
		2
Качественно эквивалентная исходной простейшая система
имеет вид

dx2

0 2

dx1

(3.7)

dx2

x .

Последняя система легко решается путем разделения переменных в каждом уравнении:

dx1	dt;	ln	x1	t ;

1			C1	1
x1

dx2	dt;	ln	x2	t ;

2			C2	2
x2

x C e 1t ;		x C		e 2t .	(3.8)
1	1	2	2

Решение в матричном виде можно записать в виде матричной экс-

поненты - матрицы eJt , которую можно найти по формуле

eJt E Jt J 2 t2 J 3 t3 ... 2! 3!

1			0		1		0		0		2
1	0	1			1	1		1			2
0	1	0		t		0		0		t		...
				t						t		...
					2!
			2				2		2

		2
1 t		1	t2 ...		0
1 t			t2 ...		0
	1	2!
	1

					2
		0		1 t	2
		0		1 t
				2	2!
					2!


			t
			t
		e	1
t2			0
t2	...		0

0 .

e 2

(3.8а)

С учетом того, что eJt удовлетворяет уравнению (3.7):

d(eJt ) J eJt dt ,

решение записывается в виде

e 1t

X eJt X

0 0

0 e 2t

	0		0
x1		x1

	0		0

x		x
x	2	x	2
	2		2

e 1t

e t (3. 8б)

												49
	x 0
Здесь		1		- матрица начальных условий.
Здесь				- матрица начальных условий.
		0
	x2
Фазовый портрет системы (3.7) зависит от знака собственных
значений	1,	2 . Уравнения фазовых траекторий имеют вид:
											dx2 2						x2
											dx							x	.	(3.9)
										1				1			1
Решая уравнение (3.9), получаем
								dx2					2			dx1

								x	2							x
									2	1				1
				x2		2	ln x ,								x Cx 2 / 1 .
		ln				2														(3.10)


				C					1					2			1
					1									1 2 0 фазовый
					1
Из	(3.10)		следует, что							при										портрет в

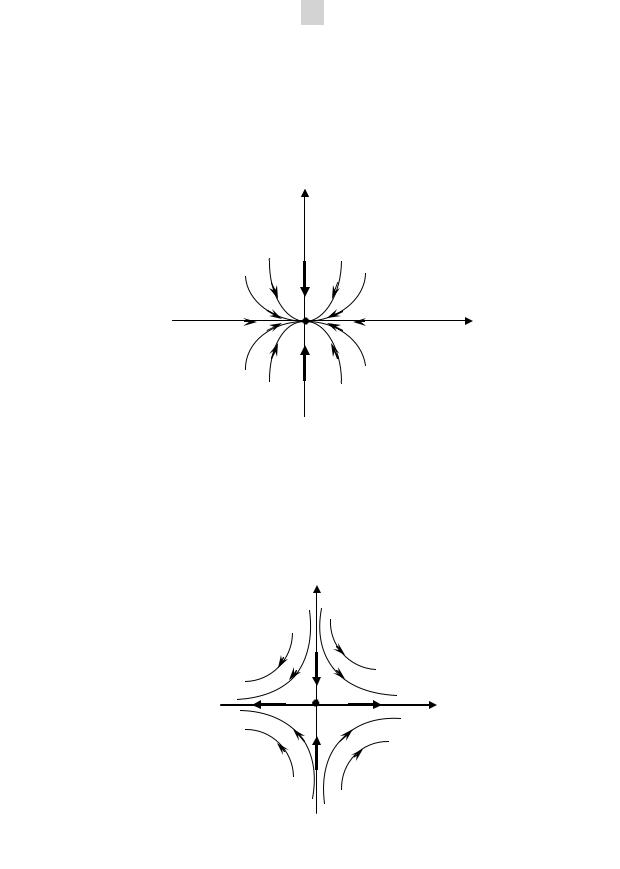
окрестности неподвижной точки x1 = x2 = 0 будет «неустойчивым узлом» (рис. 3.4).

Рис. 3.4. Фазовый портрет системы (3.7) для 1 2 0 («не-

устойчивый узел»)

При условии 2 1 0 фазовый портрет системы (3.7) в

окрестности неподвижной точки x1 = x2 = 0 будет «устойчивым уз-

лом» (рис. 3.5).

Рис. 3.5. Фазовый портрет системы (3.7) для 2 1 0 («устой-

чивый узел»)

Рис. 3.6. Фазовый портрет системы (3.7) для 2 0 1

(«седло»)

<<< < Предыдущая 1 2 3 45 / 165 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в папке Матика 2 курс

#
10.05.20152.24 Mб22Дифференциальные уравнения 2б.pdf
#
10.05.20151.59 Mб38Специальные главы математики 140410(ЭАб).pdf
#
10.05.201521.98 Кб11структура и содержание дисциплины.docx
#
10.05.20154.36 Mб43Фурье Лаплас.doc
#
10.05.2015266.24 Кб26ЭА спец глав матем практика.docx