§ 11. Колебания

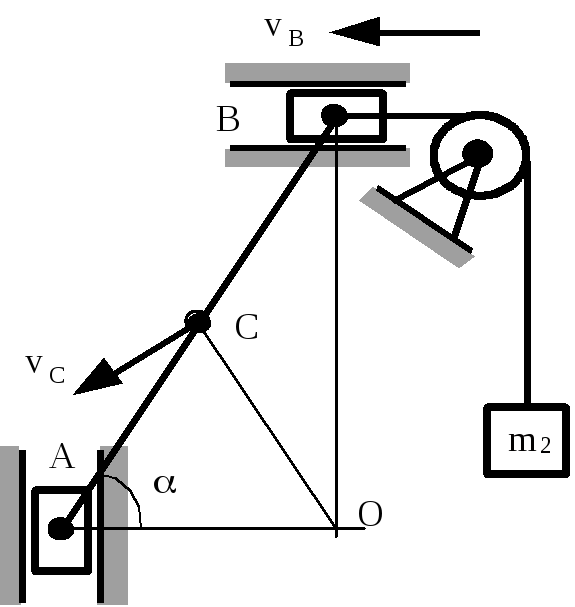
 Пример 11.1. Однородный стержень AB массой m и длиной 2l может скользить своими концами A и B по гладким взаимно перпендикулярным направляющим (рис. 76). В точке B к стержню прикреплена нить, перекинутая через идеальный блок, к другому концу которого присоединен груз массой m₂ = m₁. Определить угол ₀ , при котором система находится в равновесии, и период T малых колебаний около этого положения. Массой ползунов и блока пренебречь.

Решение.

Рис. 76

Функция Лагранжа осциллятора при малых отклонениях от положения равновесия имеет вид:

L = T – U = m_q ² / 2 – k_q q² / 2 , (11.1)

где T – кинетическая энергия, U – потенциальная функция (потенциальная энергия системы «груз – Земля», а q – обобщенная координата. Незначительное отклонение от положения устойчивого равновесия приводит к гармоническим колебаниям с периодом

T = 2  . (11.2)

Таким образом, анализ возможных колебаний сводится к определению положения устойчивого равновесия и нахождению для него величин

m_q = = и k_q = – = . (11.3)

В данной задаче

T = m₁ v_C² / 2 + J ² / 2 + m₂ v_B² / 2 , (11.4)

где v_C – скорость центра масс стержня, v_B – скорость груза m₂ , равная скорости точки B, J = m₁ l² / 3 – момент инерции стержня относительно центра масс.

Потенциальная энергия равна работе сил тяжести при переходе системы в нулевое состояние. Приняв состояние с  =  / 2 за нулевое, получим:

U = – m₂ g 2 l cos  + m₁ g (l – l sin ) . (11.5)

Положение равновесия определяется условием = 0 . Подставляя в это условие (11.5), найдем равновесное значение = ₀ :

2 m₂ g l sin ₀ – m₁ g l cos ₀ = 0. 

tg ₀ = m₁ / (2 m₂) = 1 / ( 2 ) =/ 4 .(11.6)

В качестве обобщенных координат возьмем  , то есть q  . Тогда из (11.5), (11.3) и (11.6) получим, используя также соотношение

1 + tg² ₀ = 1 / cos² ₀ :

k_q = 2 m₂ g l cos ₀ + m₁ g l sin ₀ = m₂ g l 3 / = 3 m₁ g l . (11.7)

Поскольку величина k_q > 0, то равновесие является устойчивым (функция U() имеет минимум при  = ₀).

Входящие в выражение (11.4) скорости v_C и v_B можно выразить по формуле Эйлера, принимая во внимание, что точка O (рис. 76) является мгновенным центром вращения стержня AB:

v_C = ·OC = l; v_B = · OB = 2l sin .

Подставляя эти значения в (11.4), получим

T = 2 m₁ l^{2 2} (1 + 3 sin² ) / 3 .

Отсюда с учетом (11.6) найдем:

m_q = =m₁ l² . (11.8)

Теперь можно подставить (11.7) и (11.8) в (11.2) и получить ответ:

T = 2  = 5,08 .

 Пример 11.2. Два невесомых стержня длиной l с укрепленными на нижних концах грузами массой m могут свободно вращаться в вертикальной плоскости вокруг точек A и B (рис. 77). Стержни соединены пружиной жесткостью k на расстоянии b от верхних концов. Когда стержни расположены вертикально, нить не деформирована. Найти собственные частоты ₁ и ₂ и нормальные координаты Q₁ и Q₂ рассматриваемого осциллятора.

Рис. 77

Решение.

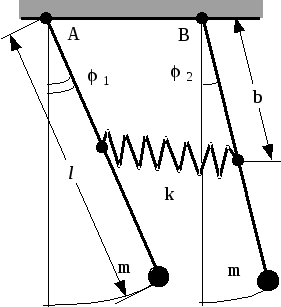
Заданная в задаче система действительно представляет собой двумерный осциллятор, поскольку она обладает двумя степенями свободы и при вертикальном положении стержней находится в устойчивом равновесии.

В качестве обобщенных координат естественно взять углы ₁ и ₂ отклонения стержней (рис. 77). Через эти координаты нужно выразить функцию Лагранжа L = T –U.

Кинетическая энергия T равна:

T = m l² (₁² + ₂²) / 2 . (11.9)

Потенциальная функция U, или потенциальная энергия системы «стержни с грузами – пружина – Земля» равна работе сил тяжести и упругости при переходе системы в нулевое состояние. Пусть в нулевом состоянии

 ₁ = ₂ = 0 .

Тогда U = m g (l – l cos ₁) + m g (l – l cos ₂) + k ( b sin ₂ – b sin ₁)² / 2 .

Если ограничиться малыми колебаниями, то последнее выражение приводится к виду:

U  (m g l + k b²) (₁² + ₂²) / 2 – k b² ₁ ₂ . (11.10)

Рассмотрим вначале стандартный метод анализа нормальных колебаний.

Находим кинематические m _{i j} и динамические k _{i j} параметры системы по формулам m _{i j} = ; k _{i j} = , где i, j = 2, 2 . Дифференцирование (11.9) и (11.10) дает:

m₁₂ = m₂₁ = 0 ; m₁₁ = m₂₂ = m l² ; (11.11)

k₁₁ = k₂₂ = m g l + k b² ; k₁₂ = k₂₁ = – k b² . (11.12)

Для нахождения собственных частот решаем вековое уравнение

(11.13)

mgl + k b2 – m l2 2	– k b2
		= 0
– k b2	m g l + k b2 – m l2 2

Det (k _{i j} – ² m _{i j}) = 0 . С параметрами (11.11) и (11.12) оно имеет вид:

Решая (11.13), находим собственные частоты, то есть частоты нормальных колебаний:

₁ = и₂ = . (11.14)

Соответствующие этим частотам нормальные координаты Q₁ и Q₂ должны удовлетворять уравнениям

 _i = A _{i } Q _ , (11.15)

где  = 1, 2, а A _{i } находится из системы

(k _{i j} – m _{i j}  _²) A _{j } = 0 . (11.16)

Подставляя в (11.16) _ = ₁, а также (11.11) и (11.12), получим:

(m gl + k b² – m l² g / l ) A₁₁ – k b² A₂₁ = 0 ,

–k b² A₁₁ + (m g l + k b² – m l² g / l ) A₂₁ = 0.

Отсюда следует, что A₁₁ = A₂₁ .

Аналогично, подставляя в (11.16)  _ =  ₂, найдем, что A₁₂ = – A₂₂.

С найденными значениями уравнения (11.15), то есть

₁ = A₁₁ Q₁ + A₁₂ Q₂ ,

₂ = A₂₁ Q₁ + A₂₂ Q₂ ,

дают:

Q₁ = (₁ + ₂) / (2 A₁₁) , (11.17)

Q₂ = (₁ – ₂) / (2 A₂₂) . (11.18)

Если Q₂ = 0, то есть  ₁ = ₂ , то в системе реализуются нормальные колебания с частотой ₁ (11.14). В этом случае пружина не деформирована, и поэтому результат такой же , как для математического маятника.

Второе нормальное колебание (при Q₁ = 0, или ₁ = – ₂) происходит с большей частотой ₂ (11.14), так как процесс убыстряется благодаря силе упругости пружины.

Рассмотрим второй способ анализа нормальных колебаний – метод приведения функции Лагранжа к каноническому виду, то есть к виду:

L = (m _{ }² – k _Q _²) / 2 . (11.19)

Сопоставляя формулы (11.9) и (11.10) с (11.19), видим, что приведение функции Лагранжа к каноническому виду сводится к такому подбору линейных комбинаций типа (11.15), при котором формула (11.10) избавилась бы от смешанных производных обобщенных координат, то есть чтобы произведение 1·2 превратилось в выражение B1 Q12 + B2 Q22 , где B1 и B2 – некоторые постоянные.

Формула разности квадратов наводит на мысль попробовать подстановку

₁ = Q₁ + Q₂ и ₂ = Q₁ – Q₂ . (11.20)

Подставляя (11.20) в (11.9) и (11.10), получим

L = m l² (₁² + ₂²) – m g l (Q₁² + Q₂²) – 2 k b² Q₂² .

Лагранжиан в координатах Q₁ и Q₂ действительно имеет канонический вид (11.19) с параметрами:

m₁ = m₂ = 2 m l² ; k₁ = 2 m g l , k₂ = 2 m g l + 4 k b² . (11.21)

Соответствующие нормальным координатам Q₁ и Q₂ частоты определяются формулой _ = . При подстановке (11.21) она дает соотношения (11.14).

Формулы (11.20) приводят к выражениям (11.17) и (11.18), полученным ранее другим способом , если положить произвольные постоянные A₁₁ = A₂₂ = 1.



Задачи для самостоятельного решения

 Задача 11.1. U- образная трубка с одинаковой площадью поперечного сечения по всей длине открыта с двух концов. Трубка содержит две несжимаемые и не смешиваемые жидкости с плотностями ₁ и ₂. Определить период  собственных колебаний системы около положения равновесия, если длина части трубки, занимаемой одной жидкостью, равна l₁, а части, занимаемой другой, – l₂.

Ответ :  = 2  .

 Задача 11.2. Однородный сплошной цилиндр радиусом r может катиться без скольжения по внутренней поверхности неподвижной трубы, радиус которой равен R. Найти период  малых колебаний оси цилиндра.

Ответ :  = 2  .

 Задача 11.3. К середине упругой невесомой горизонтально расположенной балки с коэффициентом k присоединен математический маятник массой m и длиной l. Определить собственные частоты ₁ и ₂ и нормальные координаты Q₁ и Q₂ системы.

Ответы : ₁ = ,Q₁ =  – угол отклонения маятника от вертикали; ₂ = ,Q₂ = s – смещение точки подвеса от положения равновесия.

Рис. 78

Задача 11.4. Два одинаковых однородных стержня длиной l каждый соединены между собой в точке A шарнирно, а концы B и C могут скользить без трения по горизонтальным направляющим (рис. 78). К шарниру A присоединена вертикальная пружина, длина которой в недеформированном состоянии равна l, а жесткость такова, что равновесие системы имеет место при  = 30⁰ . Определить период  малых колебаний системы около этого положения равновесия, пренебрегая массами ползунов.

Ответ :  = (4  / 3).

Рис. 79

Задача 11.5. Частица массой m находится на гладкой неподвижной горизонтальной плоскости и прикреплена к двум пружинам, концы которых закреплены неподвижно. В положении равновесия обе пружины не напряжены и образуют между собой прямой угол. Определить частоты  ₁ и  ₂ системы, ели жесткости пружин равны k₁ и k₂.

Ответ :  ₁ = ;  ₂ = .

 Задача 11.6 К*). К однородному цилиндру с моментом инерции J =  m r² и радиусом r, имеющему неподвижную горизонтальную ось вращения, прикреплены с двух сторон вертикальные упругие нити с коэффициентами жесткости k₁ и k₂ (рис. 79). Конец первой нити закреплен неподвижно в точке A, а на конце второй нити висит груз массой m. Найти собственные частоты ₁ и ₂ системы в символьном виде при k₁ = 2 k₂;  = 2. С помощью файла «Осциллятор2» вычислите значения собственных частот при k₁ = 10, k₂ = 30 и  = 2, а также  = 100.

Ответы : ₁ = ; ₂ = ;

₁ = 5,602, ₂ = 21,632 при  = 2;

Рис. 80

₁ =0,995, ₂ = 17,407 при  = 100.

 Задача 11.7 Ш. Брусок массой m скреплен пружиной жесткостью k с доской массой M (рис. 80). Доска лежит на гладкой горизонтальной плоскости. Пружину сжимают на величину x₀ и отпускают. Найти зависимость деформации x пружины от времени t.

Ответ: x = x₀ cos ( t) , где  = .

Рис. 81

Задача 11.8. На гладкой плоскости, наклоненной к горизонту на угол , находится прикрепленный к пружине, как показано на рисунке 81, брусок массой m. В положении равновесия пружина растянута на величину l. Растянув пружину на 3 l, ее отпустили без начальной скорости. Найти зависимость растяжения x пружины от времени t.

Ответ: x = 2 l cos ( t) , где  = .

Рис. 82

Задача 11.9. Определить период  малых колебаний метронома, изображенного на рисунке 82. Метроном состоит из маятника AC, центр масс которого C отстоит от оси вращения O на величину s₀, и подвижного груза G, удаленного от оси O на величину s. Момент инерции маятника относительно O равен J. Масса маятника – M, масса груза – m.

Ответ:  = 2 .

 Задача 11.10. На концах горизонтально расположенного тонкого непроводящего стержня длиной l расположены две бусинки, несущие на себе электрический заряд q₁ каждая. Третья такая же бусинка с зарядом q свободно надета на стержень и помещена посредине. Смещение бусинки из средней точки приводит к ее колебаниям . Найти период  этих колебаний, считая их малыми.

Рис. 83

Ответ:  =  l.

 Задача 11.11. Шар массой m, укрепленный на верхнем конце невесомого стержня длины l, зажат между двумя горизонтальными пружинами жесткостью k с закрепленными концами (рис. 83). Стержень может свободно поворачиваться вокруг неподвижной нижней точки. Считая пружины в положении равновесия не напряженными, найти период  колебаний системы.

Ответ:  = 2  / .

Рис.84

Задача 11.12. Однородный стержень массой m и длиной l шарнирно закреплен в точке O и удерживается в горизонтальном положении при помощи вертикальной пружины с жесткостью k, прикрепленной в точке M к стержню на расстоянии а от точки O (рис. 84). Определить период  малых колебаний стержня в вертикальной плоскости.

Ответ:  = 2  .

 Задача 11.13.К. Груз массой M = 0,5 кг прикреплен к вертикально расположенной пружине жесткостью С = 10 Н/м. К грузу снизу подвешена аналогичная система с M1 = 2 M и C1 = 2 C. Проанализируйте колебания рассматриваемой системы с помощью файлов «Изучение МО» и «Функция Лагранжа». Запишите периоды T1 и T2 нормальных колебаний и функцию Лагранжа L в каноническом виде.

Ответы: T1 = 0,727 c, T2 = 2,714 с;

L = 0,429 vq1² – 32,055 q1² + 0,634 vq2² – 3,397 q2².