Б. В. Селюк

ЗАДАЧИ

по классической механике

Смоленск

2005

Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Смоленский государственный педагогический университет

Кафедра физики

Б. В. Селюк

Задачи

по классической механике

Учебное пособие

Издательство

Смоленского государственного

педагогического университета

2005

УДК 531 (075)

ББК Б.22.22я73

С 28

Рецензент

Е. А Царева, кандидат технических наук, доцент

Смоленского государственного педагогического университета

Селюк, Б. В.

Задачи по классической механике: Учебное пособие. – Смоленск: СГПУ, 2005. – 76 с.

П

С 28

особие адресовано студентам физмата, изучающим раздел «Классическая механика» курса теоретической физики. В этом пособии студенты найдут необходимый на практических занятиях и для самостоятельной работы материал, который научит их применять на практике изучаемые теоретические положения. По каждой теме приводятся поучительные примеры, условия задач для самостоятельного решения, а также для индивидуальных письменных работ. Некоторые задачи предназначены для решения с помощью компьютера.

УДК 531 (075)

ББК Б.22.22я73

© Селюк, Б.В., 2005.

© Издательство СГПУ, 2005.

Предисловие

Решение задач является важной составной частью изучения студентами классической механики. Оно позволяет не только лучше уяснить и запомнить теоретические положения, но и помогает развить необходимые учителю физики навыки анализа механических систем и грамотного применения физических законов при их описании. Кроме того, многие идеи и методы, используемые при решении задач классической механики, применяются и в школьной физике.

Большая часть задач, включенных в настоящее пособие, заимствована из других источников, в частности, из задачников [1] и [2], а также из [3]. Тексты условий ряда задач несколько изменены с учетом профессиональной ориентации студентов физмата.

Прежде чем решать задачи по той или иной теме, студенту следует, разумеется, изучить соответствующий теоретический материал. Можно воспользоваться, например, пособием [4], содержащим необходимые теоретические сведения. Приводимые в настоящей брошюре примеры иллюстрируют методы решения типичных задач.

Работа с примерами должна строиться следующим образом. Вначале следует попытаться решить задачу, прочитав только ее условие. При возникновении затруднений нужно познакомиться с приведенным решением. После этого необходимо самостоятельно решить задачу и сверить найденное решение с образцом. Наконец, следует подготовиться к ответам на следующие вопросы, относящиеся к разбираемому примеру:

1. Перескажите условие задачи и сделайте рисунок.

2. Проанализируйте содержание условия и на этой основе сформулируйте план решения.

3. Дайте обоснование используемого соотношения.

4. Получите те или иные промежуточные результаты или ответ (по требованию преподавателя).

5. Какие идеи и приемы решения можно использовать при решении других аналогичных задач?

Из числа задач для самостоятельного решения формируются индивидуальные задания письменных контрольных работ. Их содержит таблица в конце брошюры.

Письменные работы выполняются в отдельной тетради. В этих работах приводятся решения задач с подробными пояснениями. По мере прохождения соответствующей темы, тетради с очередной шестеркой решенных задач сдаются на проверку.

Задачи, помеченные значком «Ш», – школьные. Они должны быть решены на доступном школьнику уровне. Значком «*)» помечены задачи, которыми студент может, если пожелает, заменить одну из задач своего индивидуального задания. Разумеется, замена относится к задачам из одного и того же параграфа. Значок «К» означает, что задача решается с помощью компьютера.

I. Механика ньютона

§ 1. Кинематика частицы

Рис. 1

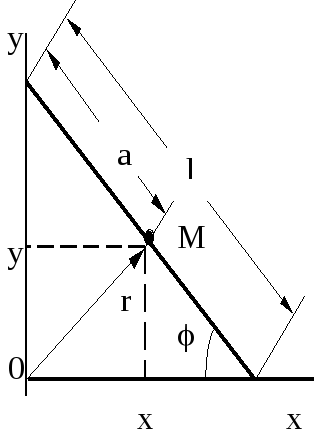
 Пример 1.1. Концы отрезка длиной l скользят по двум взаимно перпендикулярным прямым OX и OY (рис. 1). Найти траекторию, скорость и ускорение точкиM, находящейся на расстоянии a от верхнего на рисунке 1 конца отрезка. Угол  изменяется с течением времени по закону  =  t.

Решение.

Решение сводится к применению кинематических соотношений для точки M. Удобно использовать декартовы координаты x и y точки M (рис. 1).

Рис. 2

Для записи кинематических уравнений эти координаты нужно выразить через угол , зависимость которого от t задана:

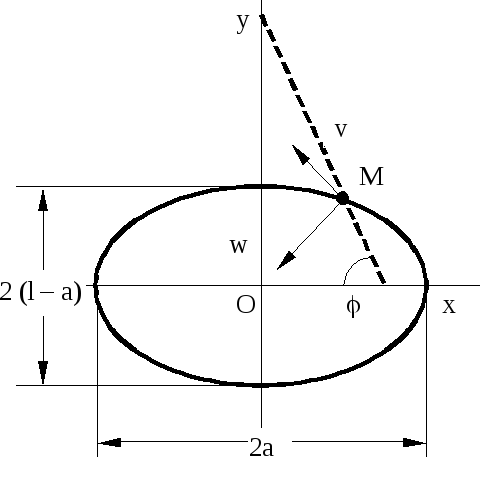
x = a cos  ; y = (l – a) sin  .

Получим:

x = a cos ( t) ; (1.1)

y = (l – a) sin ( t) . (1.2)

Чтобы найти траекторию, следует из кинематических уравнений (1.1) и (1.2) исключить параметр t:

. (1.3)

Траектория имеет вид эллипса с полуосями a и l – a. Он изображен на рисунке 2.

Проекции скорости находятся дифференцированием (1.1) и (1.2):

= – a sin ( t) , (1.4)

= ( l – a) cos ( t) . (1.5)

При 0 <  t < / 2 проекция скорости < 0 , а> 0. Это соответствует направлению скорости, показанному на рисунке 2. Модуль скорости

v = =  . (1.6)

Дифференцируя (1.4) и (1.5) и сравнивая результаты с (1.1) и (1.2), получим для проекций ускорения:

w_x = = – ² x , (1.7)

w_y = = – ² y . (1.8)

Видно, что проекции ускорения отличаются от проекций вектора(рис. 2) множителем². Это определяет показанное на рисунке 2 направление вектора . Модуль ускорения

w = = ² = ² r . (1.9)

 Пример 1.2. Найти траекторию, которую опишет корабль, сохраняющий постоянный угол  между направлением скорости и направлением на некоторый пункт О (рис. 3). В начальный момент расстояние корабля от пункта О равно ₀.

Рис. 3

Решение.

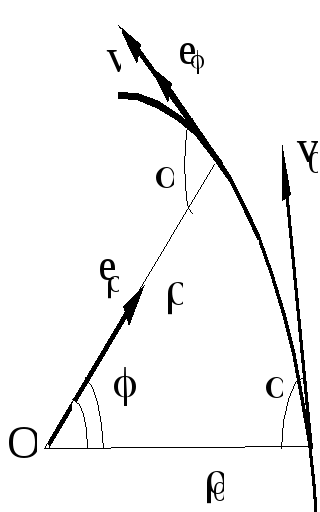
При решении этой кинематической задачи удобно использовать полярные координаты  и  (рис. 3). В этих координатах скорость определяется формулой

= + . (1.10)

Здесь иединичные орты, соответствующие полярным координатам.

Проекция скорости на направление, то есть=может быть выражена через фиксированный угол:

= – v cos  = – cos. (1.11)

Уравнение (1.11) содержит в неявном виде искомую зависимость от. Возведя это уравнение в квадрат, получим:

sin²  = ² cos²  . (1.12)

Теперь можно извлечь квадратный корень и умножить полученное равенство на величину dt, которая не равна нулю:

d = – d  ctg  . (1.13)

В выражении (1.13) оставлен лишь один из двух знаков, получающихся при извлечении квадратного корня. Именно этот знак обеспечивает уменьшение  при положительных d и ctg , как это должно быть в соответствии с исходными формулами (1.11) и (1.10).

Остается проинтегрировать уравнение (1.13) при начальном условии _=0 = ₀ :

 = ₀ exp (– ctg ) . (1.14)

Это и есть искомое уравнение траектории. При  =  / 2 траектория – окружность с радиусом ₀ и с центром в точке О. При  >  / 2 величина  возрастает с ростом  – получается раскручивающаяся логарифмическая спираль. При  = 0 или  =  угол  может быть равным только нулю – корабль движется по прямой, соединяющей его с пунктом О.

Рис. 4

 Пример 1.3. На проволочной окружности надето колечко M. Через него проходит стержень OA (рис. 4), который вращается вокруг точки О с угловым ускорением k cos  (k – постоянная величина). Определить скорость и ускорение колечка М как функцию угла . В начальный момент (t = 0) угол  и угловая скорость стержня равнялись нулю. Радиус окружности – r, 0     .

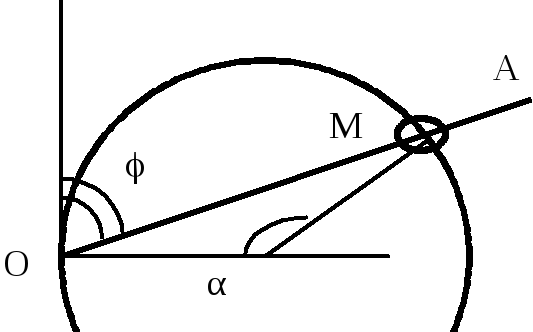
Решение.

Поскольку траектория, по которой движется колечко, известна – окружность, то целесообразно воспользоваться траекторным методом описания движения частицы.

В качестве траекторной координаты возьмем путь, проходимым колечком. Выразим этот путь через угол (рис. 4):

S = r  = r ( – 2 ( / 2 – ) ) = r 2  . (1.15)

Скорость колечка находится дифференцированием (1.15):

v = = 2 r= 2 r.(1.16)

Величину можно определить из заданного в задаче углового ускорения:

= k cos  . (1.17)

Преобразуем левую часть последнего уравнения следующим образом:

= = .

После этого уравнение (1.17) легко интегрируется:

=  = ±.

Следует оставить лишь знак «+», так как по условию задачи угол  увеличивается. После подстановки последнего выражения в (1.16) получим

v = 2 r . (1.18)

Ускорение колечка имеет две составляющие_n и _ . Поэтому

w = . (1.19)

Обе составляющие ускорения могут быть найдены с помощью формул (1.18) и (1.16):

w_n = v² / r = 8 r k sin  ,

w_ = = 2 r = 2 r k cos  .

Подставляя найденные значения в (1.19), получим ответ:

w = 2 k r .



Задачи для самостоятельного решения

 Задача 1.1. По данным уравнениям движения частицы (величины заданы в единицах СИ) найти ее траекторию в плоскости xoy и начальное положение. Нарисовать эту траекторию и указать направление движения частицы в начальный момент времени.

а) x = 3 cos t ; y = 3 – 5 sin t .

б) x = a (sin (k t) + cos (k t)) ; y = b (sin (k t) – cos (k t)) .

в) x = a + r cos ( t ) ; y = r sin ( t ) .

г) x = 2 sin (t²) ; y = 3 cos (t²) .

д) x = 3 t ; y = 6 t – 5 t² .

е) x = 3 tg (t / 2) ; y = cos t . ( t <  ) .

ж) x = 4 sin (2 t) ; y = 2 cos t . ( t <  ) .

з) x = 2 tg (t / 2) ; y = 3 sin t .

Рис. 5

и) К*). x = x₀ sin(2  t / T + ₀); y = y₀ sin(2  n t / T). Константы x₀, y₀, T – положительные числа, n – целое число. Исследовать движения при: n = 1, ₀=  / 4; n = 2, ₀=  / 2; n = 3, ₀=  / 4. Можно воспользоваться файлом «X(t)Y(t)».

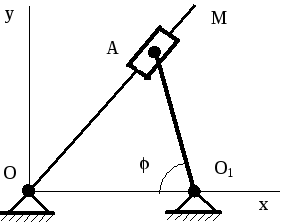
 Задача 1.2. Изображенная на рисунке 5 кулиса OM длиной l приводится в движение кривошипом O₁A, угол поворота которого  = k t (k – постоянная). Определить скорость v и ускорение w точки M, если O₁O = O₁A..

Ответы : v = k l / 2 ; w = k² l / 4 .

 Задача 1.3. Самолет равномерно набирает высоту, поднимаясь на высоту h = 7,00 км за время t = 1 мин 40 с и движется при этом со скоростью v = 900 км/ч по винтовой линии, расположенной на вертикальном цилиндре радиусом R =10 км. За самолетом следит луч радиолокатора, помещенного на оси винтовой линии. С какой быстротой должен при этом изменяться угол поворота антенны вокруг вертикальной оси?

Ответ : =  2,4·10^–2 с^–1.

 Задача 1.4. Движение частицы задано кинематическими уравнениями в полярных координатах:  = ₀ exp (t) ,  = t, где  и ₀ – постоянные. Найти траекторию и для произвольного момента времени t скорость v, ускорение и радиус кривизны траекторииR.

Ответы : Траектория – логарифмическая спираль;

v =   ; = 2²  ;R =  .

 Задача 1.5 Ш. На горе с уклоном  = 30 ⁰ бросают мяч с начальной скоростью v₀ = 9,8 м/с перпендикулярно склону горы. Найти время t полета мяча. На каком расстоянии s от точки бросания упадет мяч?

Указание: Решить задачу методом нахождения проекций перемещения, а также методом декартовых координат.

Ответы :

t = 2 v₀ / (g cos )  2,3 с ; s = 2 v₀² sin  / (g cos²)  13 м.

Рис. 6

Задача 1.6. Два стержня OA и O₁B (рис. 6), соединенные крестообразным ползуном D, могут вращаться вокруг точек O и O₁, соответственно, образуя между собой все время угол 90⁰. Определить скорость v и ускорение w точки D, если OO₁ = a, угол  = k t, где k– постоянная, а t – время.

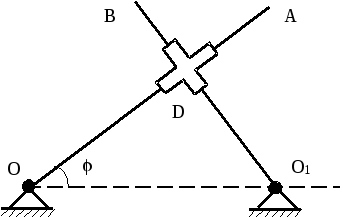
Ответы :

v = a k ; w = 2 a k².

 Задача 1.7 К. Колесо электровоза, движущегося со скоростью v = 10 м/с, имеет радиус R = 1 м. Получить траекторию точки, лежащей на расстоянии 0,5 м от оси колеса. Считая, что в начальный момент времени точка находилась в нижнем положении, указать на траектории место ее нахождения по прошествии времени t = 0,1 с; 0,2 с; 0,4 с; 0,5 с; 0,6 с. Для тех же моментов найти скорость рассматриваемой точки.

Указания.

1. Задача сводится к анализу следующих кинематических уравнений:

x = 10 t – 0,5 sin (10 t), y = 1 – 0,5 cos (10 t). Получите их.

2. Для анализа полученных кинематических уравнений используйте файл «X(t)Y(t)».

3. Зарисуйте траектории с монитора, указав на рисунке значения координат искомых точек.

4. Запишите найденные для различных моментов времени скорости в виде таблицы.

 Задача 1.8 Ш. Поезд, двигаясь под уклон, прошел за время t = 20 с путь s = 340 м и развил скорость v = 19 м/с. С каким ускорением a двигался поезд, и какова была его скорость v₀ в начале уклона?

Ответы :

a = 2 (v – s / t) / t = 0,2 м/с ; v₀ = 2 s / t – v = 15 м/с.

 Задача 1.9 Ш. Мяч бросают горизонтально со скоростью v₀ = 14 м/с с горы, составляющей угол  = 45⁰ с горизонтом. На каком наибольшем расстоянии h от поверхности горы окажется мяч во время полета? На каком расстоянии s от точки бросания он приземлится?

Ответы :

h = v₀² sin  tg  / (2 g)  7,1 м ; s = 2 v₀² tg  / (g cos )  57 м.

 Задача 1.10 Ш. Определить скорость v и ускорение a, которым обладают точки земной поверхности в Смоленске за счет суточного вращения Земли. Географическая широта Смоленска  = 55⁰.

Ответы :

v = (2  / T) R cos   2,6 · 10² м/с ; a = (4 ² / T²) R cos   1,9 · 10^–2 м/с² .

 Задача 1.11 Ш. C аэростата, опускающегося со скоростью u, бросают вертикально вверх тело со скоростью v₀ относительно Земли. Какое будет расстояние l между аэростатом и телом к моменту наивысшего подъема тела относительно Земли? Каково наибольшее расстояние l_m между телом и аэростатом? Через сколько времени  от момента бросания тело поравняется с аэростатом?

Ответы :

l = (v₀² + 2 u v₀) / g ; l_m = (u + v₀)²/ (2 g) ;  = 2(u + v₀) / g .

 Задача 1.12 Ш. Зенитная ракета стартует с поверхности Земли с постоянным ускорением a и через время  падает на Землю. Сколько времени t работал двигатель?

Ответ : t =  (1 – .

 Задача 1.13. Изображенная на рисунке 5 кулиса OM длиной l приводится в движение кривошипом O₁A, вращающимся по закону  = k t² (k – постоянная.) Составьте кинематические уравнения, описывающие движение конца кулисы M, если O₁O = O₁A.

Ответ : x = l sin (k t² / 2) ;

y = l cos (k t² / 2) .

 Задача 1.14. На проволочной окружности радиуса R = 10 см надето колечко M (рис. 7). Через него проходит стержень OA, который равномерно вращается вокруг точки O, лежащей на той же окружности. Угловая скорость  стержня такова, что он поворачивается на прямой угол за время t = 5 с. Определить скорость v и ускорение w колечка.

Рис. 7

Ответы :

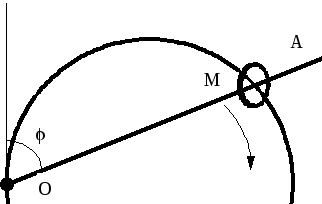
v =  R / t = 2  см/c ;

w = ² R / t² = 0,4 ² см/c² .

 Задача 1.15 . Кривошип OA (рис. 8) вращается с постоянной угловой скоростью  = 10 c^–1 . Длина OA = AB = l = 80 см. Найти траекторию средней точки M шатуна AB, а также ускорение w ползуна B в момент времени, когда угол  = 0.

Рис. 8

Ответ : w = 2 l ² = 1,6 · 10² м/с² .

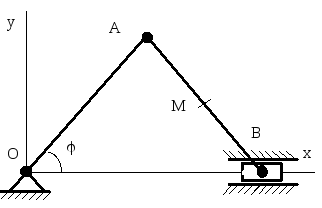
 Задача 1.16 . В кривошипно-шатунном механизме, показанном на рисунке 8, AO = AB = 60 см, MB = AB / 3,  = 4  t , где t – в секундах. Найти скорость v , ускорение w и радиус R кривизны траектории точки M в начальный момент времени.

Ответы : v = 80 · cм/с ; w = 1600·² cм/с²; R = 4 cм .

 Задача 1.17 Уравнения движения частицы в декартовой системе координат имеют вид

x = a cos (k t), y = a sin (k t), z =  t.

По какой траектории движется частица? Найдите скорость и ускорение частицы в цилиндрической системе координат.

Ответы : = k a_ +  _z , = – a k² _ .

 Задача 1.18 . Точка движется по окружности радиуса R = 10 см согласно уравнению s = 20  t² (s – в сантиметрах, t – в секундах). Определить тангенциальное w_ и нормальное w_n ускорения точки после того, как она один раз обойдет всю окружность.

Ответы : w_ = 40 ; w_n = 160 ² .

 Задача 1.19 . Движение точки задано в цилиндрических координатах уравнениями  = 2,  = t² / 2, z = t³ / 3. Все величины выражены в единицах СИ. Определить радиус R кривизны траектории в момент времени t = 1,0 с.

Ответ : R = 2,3 м.

 Задача 1.20 . Частица движется по окружности радиусом R равноускоренно из состояния покоя и совершает первый полный оборот за время T. Определить скорость v и ускорение w частицы в конце этого промежутка времени.

Ответы : v = 4  R / T; w = (4  R / T²) .

Рис.9

Задача 1.21 . Тело брошено со скоростью v₀ под углом  к горизонту. Пренебрегая сопротивлением воздуха, найти радиус кривизны траектории в момент возвращения тела к горизонтальной плоскости, в которой оно находилось в момент броска.

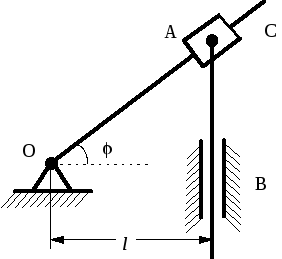
Ответ : R = v₀² / (g cos ).

 Задача 1.22 . В кулисном механизме, изображенном на рис. 9, определить угловую скорость  и угловое ускорение  кулисы OC в момент, когда угол  = 45⁰, если штанга AB движется с постоянной скоростью v, а ползун A скользит вдоль OC. Расстояние от оси вращения O до штанги AB равно l.

Ответы :

 = v cos² () / l = v / (2 l );

 = – v² cos²() sin (2) / l² = – v² / (2 l²).

 Задача 1.23 . Цепная передача велосипеда состоит из цепи, охватывающей зубчатку, приводимую в движение педалями, и шестерню, жестко связанную с задним колесом велосипеда. Зубчатка имеет z₁ = 26 зубьев, а шестерня – z₂ = 9 зубьев. Диаметр заднего колеса велосипеда D = 70 см. С какой скоростью v едет велосипедист, делающий педалями n = 1 оборот за время t = 1 секунду, если колеса катятся без проскальзывания.

Ответ : v =  n z₁ D / (z₂ t) = 22,9 км/ч.