§109 Оператор Гамильтона в методе вторичного квантования.

Мы знаем оператор

Одночастотный оператор описывает

систему независимых не взаимодей-

ствующих между собой частиц.

Взаимодействие между частицами.

Мы описываем систему Бозе-частиц. Внешнее взаимодействие входит в .

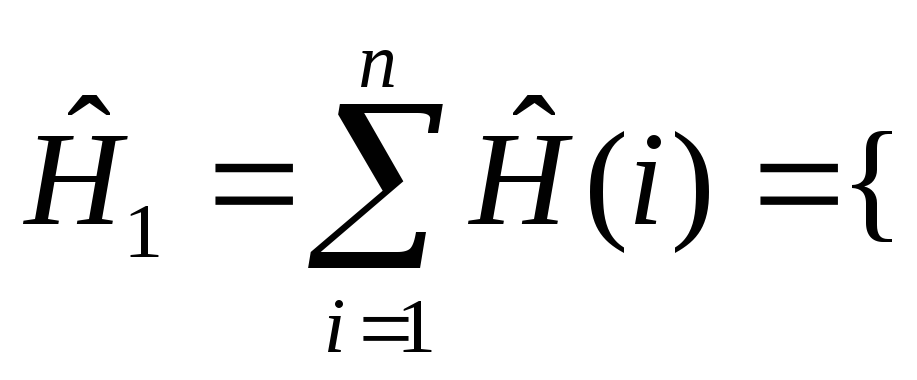в методе вторичного квантования

Запишем матричный элемент

и - одночастичные состояния: мы учтём, чтои- есть собств. Функции оoдночастичного оператора , т.е.и учтём

тогда

тогда с учётом этого имеем суммирование по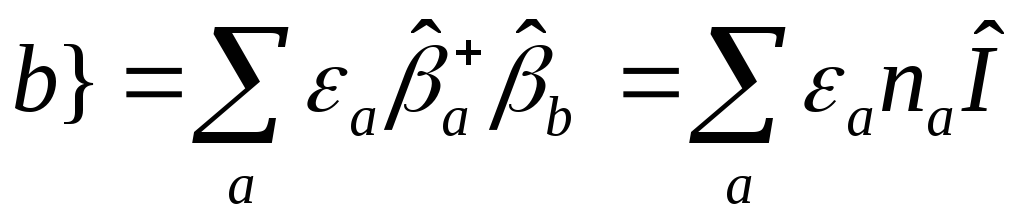- это есть энергия состояния

т.е. - это собственное значение одночастичного оператора, т.е..

Далее можно рассмотреть. Оператор взаимодействия между частицами, он рассмотрен в теории возмущений с учётом существующих только парных взаимодействий:

переходит в .

Это всё для случая статистики Бозе -Эйнштейна.

Д/з разложение по произведению одночастичных функций- по такому базису.

§110 Операторы вида и их свойства.

Часть их называют полевыми операторами или операторными функциями.

Рассмотрим оператор одночастичный, который был получен через операторы рождения и уничтожения:

(1), где матричный элемент

Подставим этот матричный элемент в сумму (1), то получим:

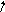
( здесь сумму разбили на 2 части)

здесь можно выделить два оператора и введём обозначения:

(2) , здесь перемен.рассмотрим в качестве параметра.

Такое разложение часто используется для мотивировки разложения по вторичному квантованию.

В (2) оператор как бы играет роль коэффициентов разложения, т.е. имеем коэффициенты – операторы.

Напомним обычное разложение по базису: .

Поэтому метод назвали методом вторичного квантования.

Найдём оператор сопряженный оператору (2):

Мы переставим местами ит.к.- это не оператор, а функция одночастичного состояния, которая является собственной функцией оператора-одночастичного оператора во внешнем поле:

.

Оператор действует на

, т.е. он действует на числа заполнения

- получили такой матричный элемент.

Идёт интегрирование по координате .

Мы свели оператор одночастичный к одному матричному элементу.

Запишем двухчастичный оператор:

(4)

={Напомним, что, где- оператор взаимодействия-той и-той частицы}=

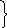
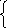
= таков вид матричного элемента, его надо вписать в (4 стр. 33а) и исп. Определение полевых =

операторов

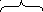
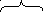
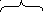
(5) - т.е. получим аналогично двухчастичного матричного элемента.

Это выражение компактно, от него можно исходить при переходе к вторичному квантованию.

А:

Теперь стоит проблема коммутации операторных функций.

Рассмотрим коммутатор

(6)

в этом коммутаторе есть функции, которые можно вынести за знак коммутатора как коэффициенты, т.к. они не принимают участия в коммутаторе – они не операторы

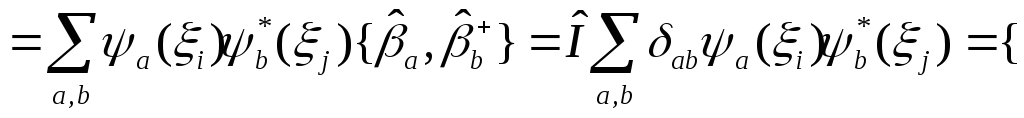
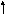суммируем по

Итак имеем

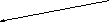Это условия коммутации

Рассмотрим оператор плотности частиц :

- это его определение.

Найдём интеграл по от этого оператора:

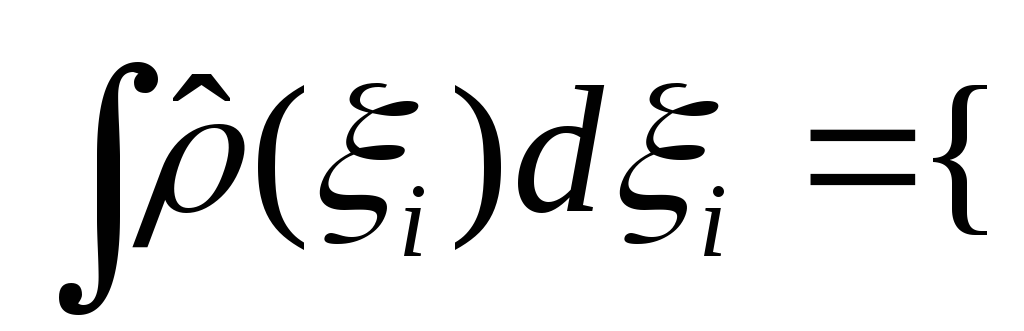далее i писать не будем, хотя не считаем заN-мерный вектор

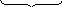
это условие ортонормированности =

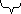
это есть оператор числа частиц в одночастичном состоянии а.

Где - оператор числа частиц в системе, тогда

, тогда есть оператор плотности

, где - объём в пространствеи одно спиновое значение.