§102Операторы рождения и уничтожения

в задаче об ЛГО (линейном гармоническом осцилляторе)

Введем оператор следующим образом:

В силу эрмитовости оператора

, найдем сопряженный этому оператору:

и:и

Посмотрим как действуют операторы ина:

Из (15): (15’)

Из (15’) и (14) мы получаем:

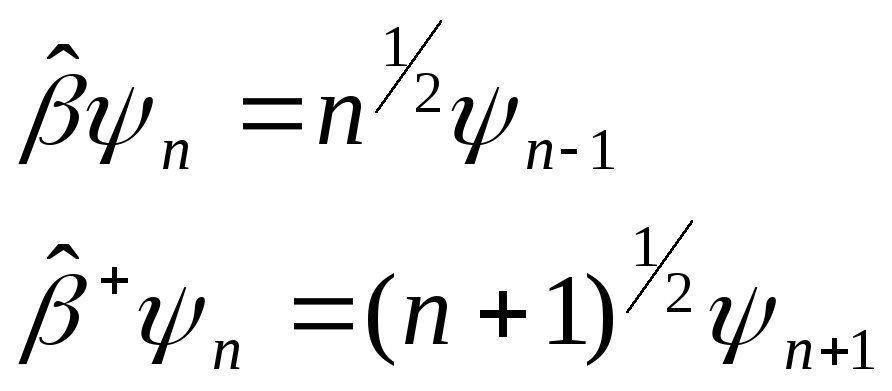(16)

Сами операторы ина себе нагрузки не несут. Но их можно интерпретировать как операторы рождения и уничтожения, т.е. имеется ансамбль одинаковых частиц с энергией, и можно осуществить переход между эквивалентными энергиями. Потому переход частицы на нижний уровень мы интерпретируем как уничтожение частицы с энергией, а переход частицы на верхний уровень мы интерпретируем как рождение частицы с квантом.

- оператор уничтожения частицы с квантом  на данном энергетическом уровне.

- оператор рождения частицы с квантом  на данном энергетическом уровне.

§103 Свойства рождения и уничтожения. Оператор .

Мы введем оператор

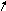
Это вид в координатном

представлении.

Действие на :

(1*)

в силу этого отношения, - оператор уничтожения.

Мы ввели понятие числа частиц n, c квантом , которые характеризуют состояние осциллятора . Это состояние мы интерпретируем как n частиц с квантом .

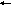
, тогда матричный элемент оператора уничтожения: это различные модификации матричного элемента , т.к. n=n₁-1 это тоже самое, что и n+1=n₁.

Наряду с этим, мы введем сопряженный оператор:

его вид в координатном представлении

Действие этого оператора на волновую функцию :

(2*)

И матричный элемент этого оператора имеет вид:

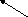
Это разные модификации

этого матричного элемента.

Очевидно, что можно получить из :

,т.к. - сопряженный к .

В силу вещественности имеем:

Рассмотрим коммутационные соотношения операторов и :

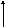
эта часть есть оператор ; т.е.,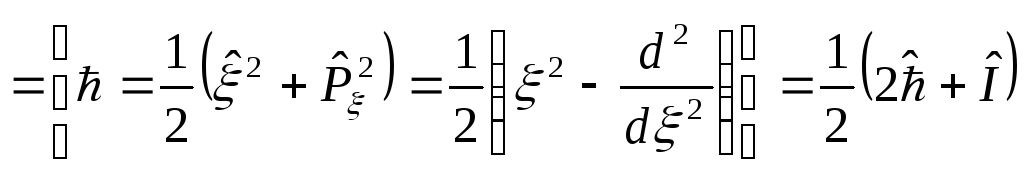

где - единичный оператор.

Рассмотрим , он равен

Н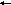айдем коммутатор:получим единичный оператор.

Выразим оператор через рождения и уничтожения:

симметризуя, получаем: , чаще используют

Найдем собственные значения для и , найдем их в матричной форме.

, тогда

Аналогично: - посмотрим на этот матричный элемент.n – это число частиц с квантом . Поэтому оператор - это оператор числа частиц: . Тогда

Посмотрим на соотношение (1*).

Подействуем: - т.е. состояние соответствует нулю частиц, это состояние вакуума или основное состояние.

Подействуем (2*):

Подействуем на : 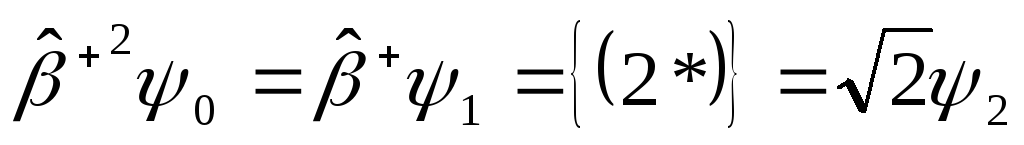и т.д.: этим

соотношением устанавливается связь между и , тогда имеем

Достаточно найти , и тогда сможем найти все остальные функции .

§104 Полином Эрмита (пэ) и функции Эрмита (фэ).

Функции - называются ФЭ, они удовлетворяют уравнению:

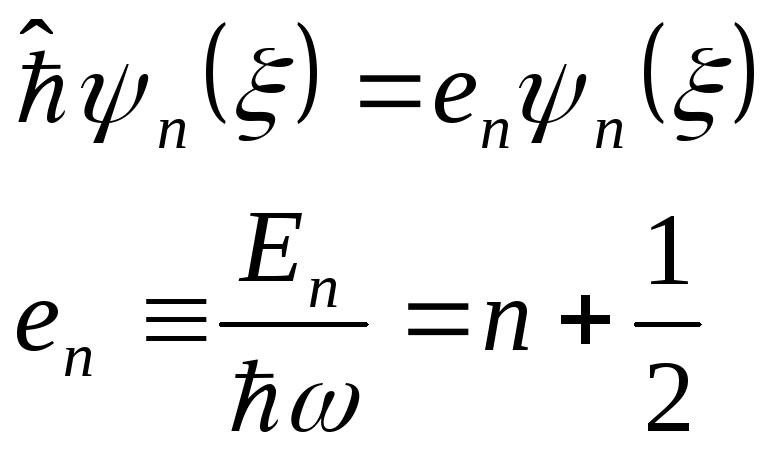
Оператор

Тогда ФЭ удовлетворяют уравнению: - это дифференциальное уравнение.

ФЭ – ортонормированны:. Скалярное произведение.

Это означает:

Теперь запишем дифференциальное уравнение, которому удовлетворяет функция , это дифференциальное уравнение 1-го порядка: , т.е. - решение этого уравнения: .

Константу C₀ найдем из условия нормировки:

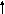
взяли Re C₀, т.к. сама - вещественная.

Тогда .

Поэтому:

Найдем функцию .

Рассмотрим коммутацию:

Но коммутатор:

Тогда:

Тогда получаем операторное равенство:

но оператор ,

тогда

Д

Легко заметить, что

ля расчета нам надо найти :

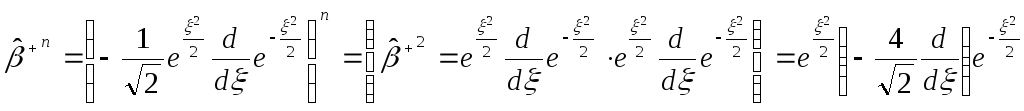
это = 1

Тогда

часто пишут: (3*)

где: - это ПЭ.

Константа C_n:

Запишем 2-3 полинома вида ПЭ:

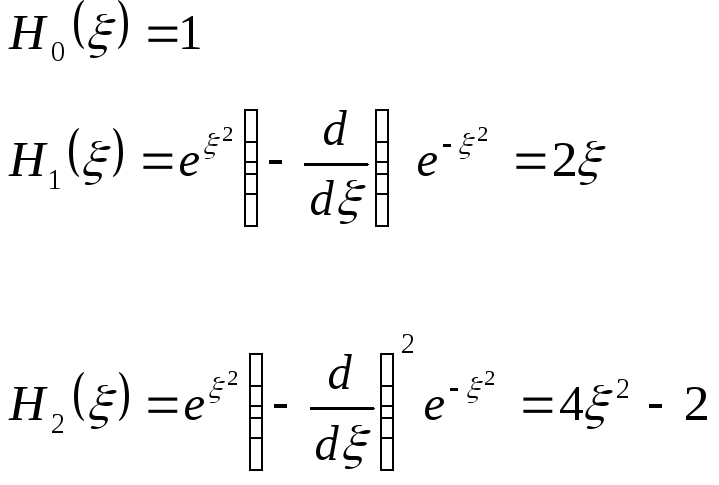
Так получаются ПЭ.

Индекс полинома n указывает максимальную степень переменной .