
- •§98 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства.
- •§99Энергетическое представление в случае дискретного спектра: методы Шредингера и Гейзенберга.
- •, ( 1 )
- •§102Операторы рождения и уничтожения
- •§103 Свойства рождения и уничтожения. Оператор .
- •§104 Полином Эрмита (пэ) и функции Эрмита (фэ).
- •Метод вторичного квантования в случае статистики Бозе-Эйнштейна (б-э).
- •§ 105 Волновая функция в - представлении:
- •§ 106 Оператор в -представлении.
- •§107 Операторы рождения и уничтожения частиц.
- •§108 Оператор в- представлении.
- •- Одночастичных состояний.
- •§109 Оператор Гамильтона в методе вторичного квантования.
- •§110 Операторы вида и их свойства.
- •Метод вторичного квантования в случае статистики Ферми-Дирака(ф-д). Основные формулы.
- •Предмет и метод статистической физики. Статистическое описание систем с большим числом степей свободы.
- •§111 Системы с большим числом степеней свободы.
- •§112 Метод статистической физики (Элементы теории вероятностей).
- •§113 Микро- и макро- параметры систем.
- •§114 Свойство эргодичности системы.
- •§115 Два способа усреднения в стат физике.
- •§116 Понятие ансамбля систем.
- •§117 Эргодическая гипотеза.
- •§118 Равновесное состояние у системы.
- •§119 Время релаксации.
- •§120 Квазизамкнутость с статическая независимость подсистем.
- •§121 Принцип равновероятности микросостояний.
- •§122 Статистический вес макросостояния.
- •§123 Статистическая энтропия.
- •§124 Теорема Лиувилля.
- •§125 Микроканоническое распределение Гиббса. Рассмотрим замкнутую систему, и согласно принципу равной вероятности, все состояния системы, с заданной энергией , равновероятны.
- •§126 Каноническое распределение Гиббса.
- •§127 Принцип возрастания энтропии.
- •Добавление к т. Лиувилля
- •Добавление к микроканоническому распределению Гиббса.
- •§128 Каноническое распределение Гиббса.
- •§129 Флуктуации аддитивных величин. Рассмотрим величины, которые для всей системы связаны с аналогичными величинами подсистем по закону суперпозиции: ,
- •Посмотрим среднее от аддитивной наблюдаемой случайной величины:
- •§§ Энтропия и статистический вес.
- •§130 Температура.
- •§131 Статистическая сумма и ее свойства.
- •§132 Функция распределения вероятностей по энергии w(e) и распределение Гаусса.
- •§133 Квазиклассическое приближение в статистической физике.
- •- Это площадка, описывающая состояние
Добавление к микроканоническому распределению Гиббса.
Аналогом соотношения
![]() является для кв. подсистем соотношение
является для кв. подсистем соотношение![]()
Для замкнутых кв.
систем энергия системы
![]() ,
тогда имеет место принцип равной
вероятности всех микросостояний, которые
отвечают данному значению энергии
системы, тогда
,
тогда имеет место принцип равной
вероятности всех микросостояний, которые
отвечают данному значению энергии
системы, тогда![]() ,
и тогда
,
и тогда
![]()
 (начало этого
вопроса стр. 44а)
(начало этого
вопроса стр. 44а)
это
вероятность реализации
![]() состояния с энергией
состояния с энергией![]()
![]() {т.
к. все состояния одинаковы}
{т.
к. все состояния одинаковы}![]()
![]() -
номер подсистемы.
-
номер подсистемы.
§128 Каноническое распределение Гиббса.

Система 1 и термостат 2 образуют замкнутую систему и микроканоническое распределение.
На базе микроканонического распределения строят макроканоническое распределение.
Также можно получить макроканонческое распределение системы через принцип возрастания энтропии.
Рассмотрим систему 1, и считаем что состояние стационарное.
Найдем
условия
![]() экстремума ф-ции
экстремума ф-ции![]() :
где
:
где![]()
мы исп.
![]() - квантовые ф-ции, т. к. это удобнее, чем
исп.
- квантовые ф-ции, т. к. это удобнее, чем
исп.![]() , т. к. при исп.
, т. к. при исп.![]() вылезает константа, которая вылезает
из-за размерности
вылезает константа, которая вылезает
из-за размерности![]() .
.
![]() - размерная величина,
а
- размерная величина,
а
![]() надо брать от безразмерной величины.
надо брать от безразмерной величины.
А
![]() - это безразмерная величина.
- это безразмерная величина.
![]()
второе
начало термодинамики:
![]() т. е., если система выведена из состояния,
то система идет в развитии с увеличением
, поэтому - имеем условие экстремума.
т. е., если система выведена из состояния,
то система идет в развитии с увеличением
, поэтому - имеем условие экстремума.
(1)
![]() - имеем условие экстремума.
- имеем условие экстремума.

отсюда
имеем задачу поиска экстремума ф-йии
![]() .
.
вероятность удовл. условию нормировки:
(2)
![]() - это условие для отыскания экстремума
.
- это условие для отыскания экстремума
.
Задача (1) и (2) является задачей поиска условного экстремума.
Однако
с помощью метода неопределенных
множителей Лагранжа можно найти
безусловный экстремум . Для этого
вводится ф-ции
![]() ,
,
где
![]() ,
,
где
![]()
Найдем
производную
![]()
(остальные члены при диф. обращаются в 0)
Найдем 2-ые производные:
![]() ,
при
,
при
![]()

![]() это выражение
отрицательное.
это выражение
отрицательное.
столь быть мы имеет , т. к. II производная <0.
Тогда
из условия
![]() находим само условие экстремума
находим само условие экстремума
![]()

![]() это константа
находится из условия нормировки
это константа
находится из условия нормировки
![]() , где
, где![]() - число всех состояний
- число всех состояний
это есть принцип равной вероятности для замкнутых системы; это есть микро каноническое . распределение.
Теперь найдем экстремум энтропии при двух условиях, а именно при
(1)
![]() и (2)
и (2)![]()
Переходим
от условного экстремума энтропии к
безусловному экстремуму ф-ции
![]() :
:![]()
ищем абсолютный экстремум этой ф-ции
Берем производные:
![]() это условие экстремума
это условие экстремума
![]() ,
это одно и тоже
,
это одно и тоже
обозначим
что условие
экстремума для
![]()
это
![]() при условиях (1) и
(2)
при условиях (1) и
(2)
Тогда
имеем:

Отсюда
для
![]() (3)
(3)
Постоянная
![]() находится
из условия нормировки, мы получим:
находится
из условия нормировки, мы получим:
![]() =1
,тогда
=1
,тогда
![]()
это выражение наз. статистической суммой.
Тогда
const
![]() есть
статистич. сумма.
есть
статистич. сумма.
Это распределение (3) относится к системе


, где 1 находится в тепловом контакте с термостатом 2.
(3)-это Константа распределения Гиббса.
Микроканоническое
распределение мы получали для замкнутых
систем, где
![]() ,
т. е. условия
,
т. е. условия
![]()
 выражаются
выражаются
![]()
в
одно условие
![]()
и для
микроканоническое. распределение мы
получили
![]()
а каноническое распределение получили когда система 1 была в тепловом контакте с термостатом 2, и получили
![]()
const
![]() находится из условия
находится из условия
![]() ,
т. е.
,
т. е.![]() ,
,
здесь
![]() -это
среднее значение энергии, т. к. у нас
случай термодинамики.
-это
среднее значение энергии, т. к. у нас
случай термодинамики.
Найдем связь энтропии с энергией:

 тогда
тогда
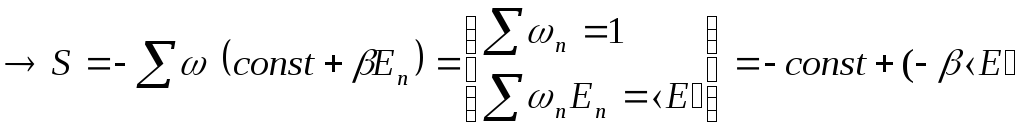
это
![]() по
энергии.
по
энергии.
В
термодинамике
![]() -
это наблюдаемая величина, поэтому пишут
эту величину просто
-
это наблюдаемая величина, поэтому пишут
эту величину просто![]() ,
т. к.
,
т. к.

 А набл.
А набл.
![]()
Это из эксперимента это из теории
Т огда
огда![]()
Это из термодинамики.
тогда
![]() ,
но
,
но![]() ,
тогда
,
тогда
![]()

![]() мы
определили тогда второй неопределенный
мы
определили тогда второй неопределенный
множитель Лагранжа.
тогда каноническое распределение Гиббса имеет вид:
![]() ,
где
,
где
![]()
Аналогично
пишут для
![]() ,
но для
,
но для![]() вместо стат. суммы
вместо стат. суммы![]() будет интеграл.
будет интеграл.
![]() -температура
в энергетических единицах.
-температура
в энергетических единицах.
