2.3 Эпюры точек, расположенных в четвертях пространства

Плоскости π1 и π₂ делят пространство на четыре четверти, которые принято нумеровать так, как показано на чертеже 10.

Ось проекций X делит π1 и π₂ на две полуплоскости, которые обозначаются соответственно: π1 и -π1 ; π₂ и - π₂ . Зритель условно находится в первой четверти. Плоскости считаются непрозрачными, поэтому видно только то, что находится в первой четверти.

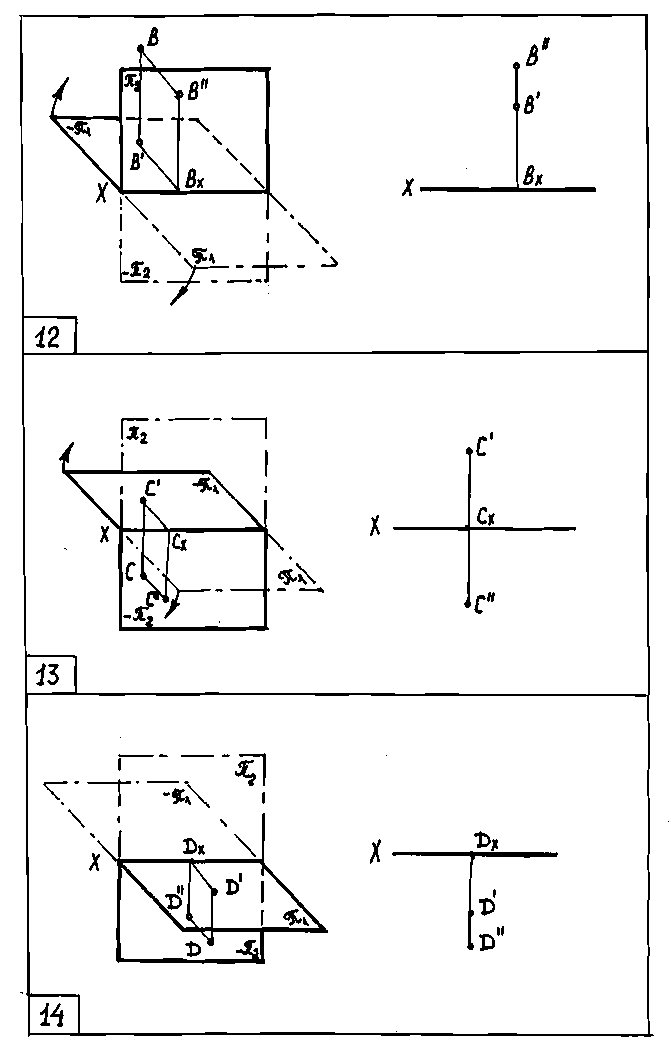
При переходе от пространственного изображения к эпюру, т.е. при совмещении горизонтальной плоскости проекций с фронтальной, передняя полуплоскость π1 будет вращаться на 90° вокруг оси X вниз, а задняя (-π1) - вверх. Поэтому горизонтальные проекции точек, лежащих во II-й и III-й четвертях, будут находиться над осью X, а фронтальные проекции точек III-й и IV-й четвертей под осью X (черт. 11, 12, 13, 14). Независимо от того, как изменяется положение проекций точки относительно X, горизонтальная и фронтальная проекции обязательно лежат на одном перпендикуляре к оси X.

2.4 Эпюры точек, расположенных в октантах пространства

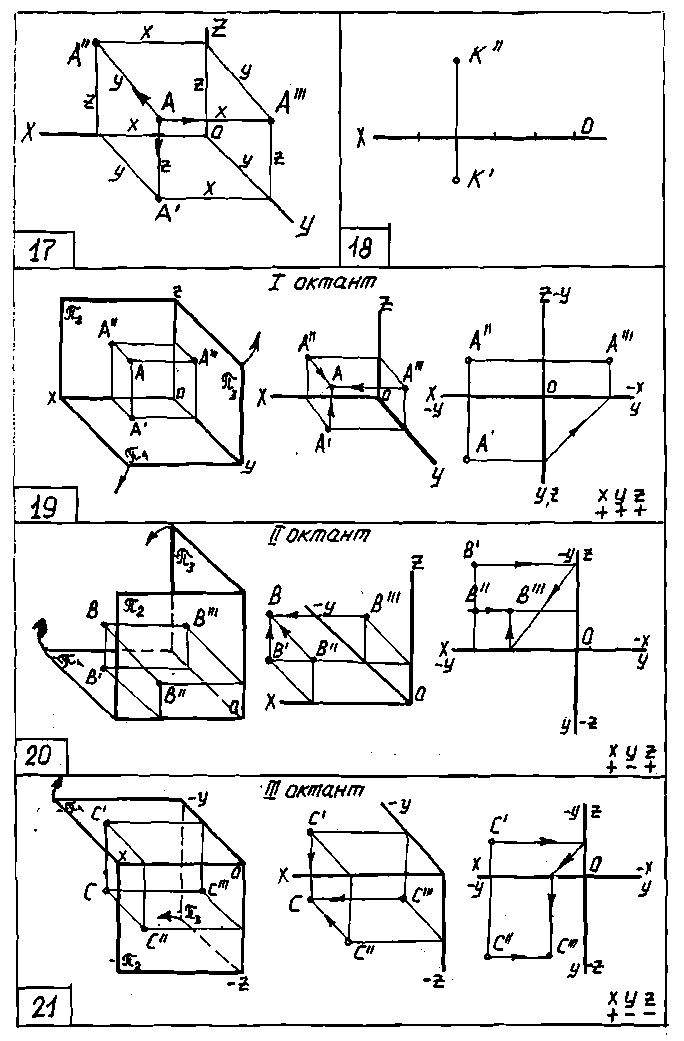
Плоскости проекций, π1, π_2, π₃ в своём пересечении образуют восемь трёхгранных углов - восемь октантов. Нумерация октантов указана на чертеже 15. Октанты с I-го по IV -й нумеруются подобно четвертям, октанты с

V-го по VШ-й аналогично, с той лишь разницей, что они располагаются за профильной плоскостью проекций.

Точка пересечения осей проекций О принимается за начало координат, поэтому X, У и Z могут быть как положительными, так и отрицательными (см. черт.15). При переходе к плоскому изображению учитываем вращение плоскостей проекций π1 и π₂. Особенно важно запомнить, что фронтальная плоскость проекций π₂ (вместе с фронтальными проекциями) всегда остаётся на месте. π1 вращается вокруг оси Х на 90°, а π₃ - вокруг оси Z также на 90°.

Полученное таким образом совмещение трёх плоскостей проек­ций (черт.16) является плоской моделью системы трёх пространственных координатных плоскостей.

На чертеже 17 построена в пространстве точка А по её координатам X, У, Z. Из приведённого изображения видно, что каждая проекция точки определяется двумя координатами: А' (X, Y); А" (X, Z); А"' (Y, Z). Следовательно, по координатам точки X, Y, Z может быть построен эпюр.

На чертеже 18 приведён эпюр точки К (3; 1; 2) в системе π1 / π_2, построенный по её координатам. Особо подчёркиваем: две проекции точки однозначно определяют её положение в пространстве.

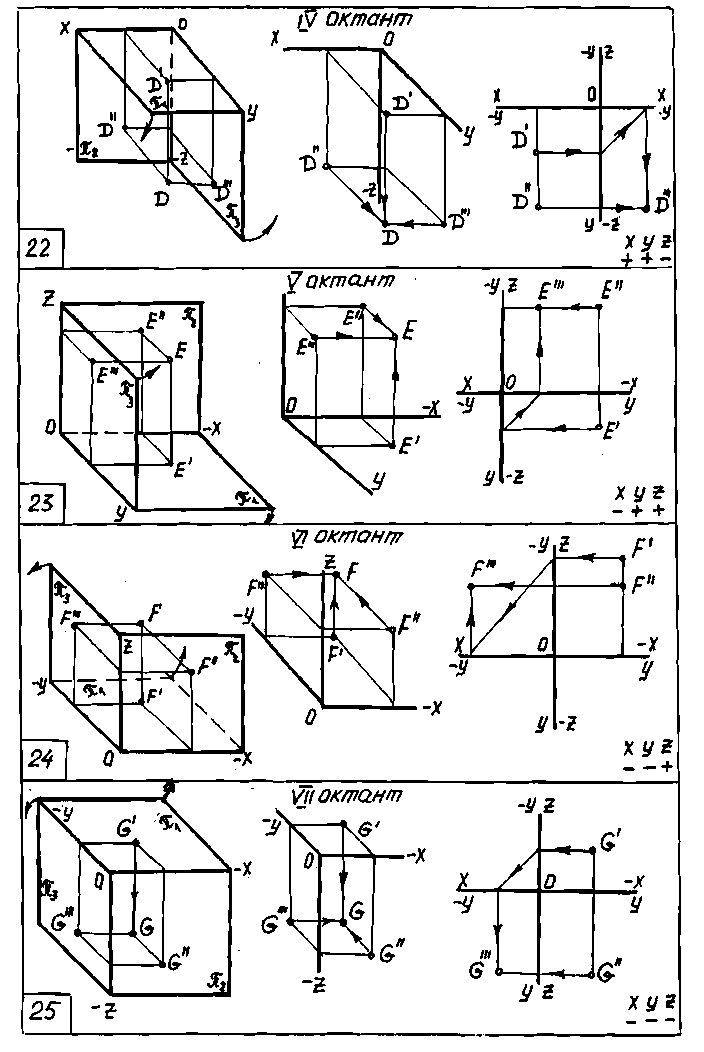
Следовательно, по двум (любым) проекциям точки можно определить её координаты Х,Y,Z, построить третью проекцию и аксонометрическое (наглядное) изображение точки в пространстве. На чертежах 19-26 приведены эпюры точек для восьми октантов, даны наглядные изображения, при построении которых размеры по оси ординат Y сокращены в два раза (М 1:2) в соответствии с правилами построения фронтальной диметрической проекции (ГОСТ 2.317-69). На этих чертежах приведены также знаки координат точек.

3 Прямая

3.1 Проекции отрезка прямой

По инвариантному свойству параллельного проецирования проекция

прямой есть прямая. Имея две точки, можно построить прямую линию.

Следовательно, имея проекции этих точек на плоскости π1, π_2, π₃ можно построить проекции прямой линии на эти плоскости (соединив одноимённые проекции точек).

На чертеже 27 приведено наглядное изображение прямой АВ с её проекциями: А'В' - горизонтальной; А"В"- фронтальной и А'"В'" - профильной. Эпюр этого отрезка изображён на чертеже 28. Отрезок АВ не параллелен ни одной из плоскостей проекций. Это отрезок прямой общего положения.

У отрезка прямой общего положения

А'В'<АВ; А"В"<АВ; А'"В'"<АВ,

т.е. каждая из его проекций меньше истинной величины самого отрезка.