3.4 Следы прямой линии

/ Точки пересечения некоторой прямой линии (а) с плоскостями проекций называют следами прямой линии (черт. 44):

H ( Н', Н", Н"') -горизонтальный след

F (F', F", F"') - фронтальный след

Р (Р',Р",Р'") - профильный след.

Горизонтальная проекция ( H') горизонтального следа (Н) все­гда совпадает с самим следом, т.е. H = H' (Z=0) соответственно,

F=F" (Y=0), Р=Р'"(Х=О).

Для того чтобы найти горизонтальный след, необходимо (черт. 45):

1) отметить точку пересечения фронтальной проекции прямой с осъю Х;

2) через полученную точку Н" провести прямую (b), перпендикулярную к оси Х;

3) пересечь перпендикуляр b с горизонтальной проекцией прямой а', отметить точку их пересечения как горизонтальную проекцию горизонтального следа.

Для того чтобы найти фронтальный след Р , применяем это же правило.

Сам профильный след всегда лежит на профильной проекции прямой и совпадает со своей профильной проекцией.

Три следа (Н,F,Р) имеет только прямая общего положения. Следует иметь в виду, что прямая, параллельная какой либо плоскости проекций, следа на эту плоскость иметь не может, т.к. она с ней не пересекается (черт. 46, 47).

В начертательной геометрии считается, что наблюдатель распо­ложен в

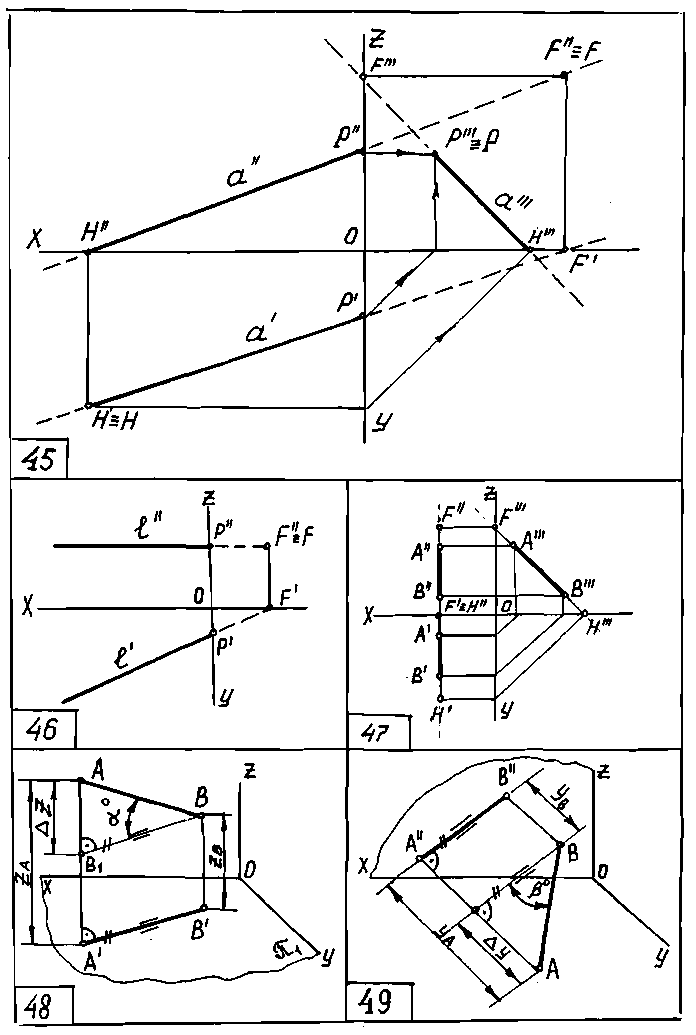
первой четверти (первом октанте), поэтому видимыми геометрическими фигурами будут только те, которые расположены в 1-м октанте, проекции этих фигур показываются сплошными линиями. Фигуры, расположенные в других пространственных частях, не видны наблюдателю, и их проекции показываются штриховыми линиями (черт. 45, 46, 47).

Каждый след прямой изменяет её местоположение в пространстве, т.е. прямая переходит из одного октанта в другой. Ход прямой дает информацию о "путешествии" прямой в пространстве. Прямая на чертеже 45 берёт начало в бесконечности пространства IV-го октанта. Горизонтальный след H "переводит" прямую в I-й октант, профильный след Р - в V-й октант, а фронтальный след F - из V-го в VI-й.

3.5 Построение на эпюре натуральной величины отрезка прямой общего положения

На чертеже 48 показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А'В'. Проведя прямую ВВ₁, параллельную горизонтальной проекции отрезка А'В' ( В₁ || А ' В'), получим прямоугольный треугольник АВВ_1.

Длина отрезка АВ равна гипотенузе этого треугольника, катета­ми которого являются: ВВ₁ = А'В' и разность координат Z точек А и B (∆Z=Z_a-Z_B).

Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и её проекцией на плоскость (А'В'). Следовательно, угол треугольника АВВ₁, лежащий против катета ∆R, равен углу наклона отрезка АВ к горизонтальной плоскости проекций π₁ (угол α °).

Аналогично рассуждая (черт. 49), можно показать, что длина от­резка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А"В" и разность координат Y точек А и В (∆Y = Y_A – Y_B). Угол этого треугольника, лежащий против катета ∆Y , равен углу наклона отрезка АВ к фронтальной плоскости проекций π₂.

По аналогии длина отрезка АВ может быть определена и как ги­потенуза

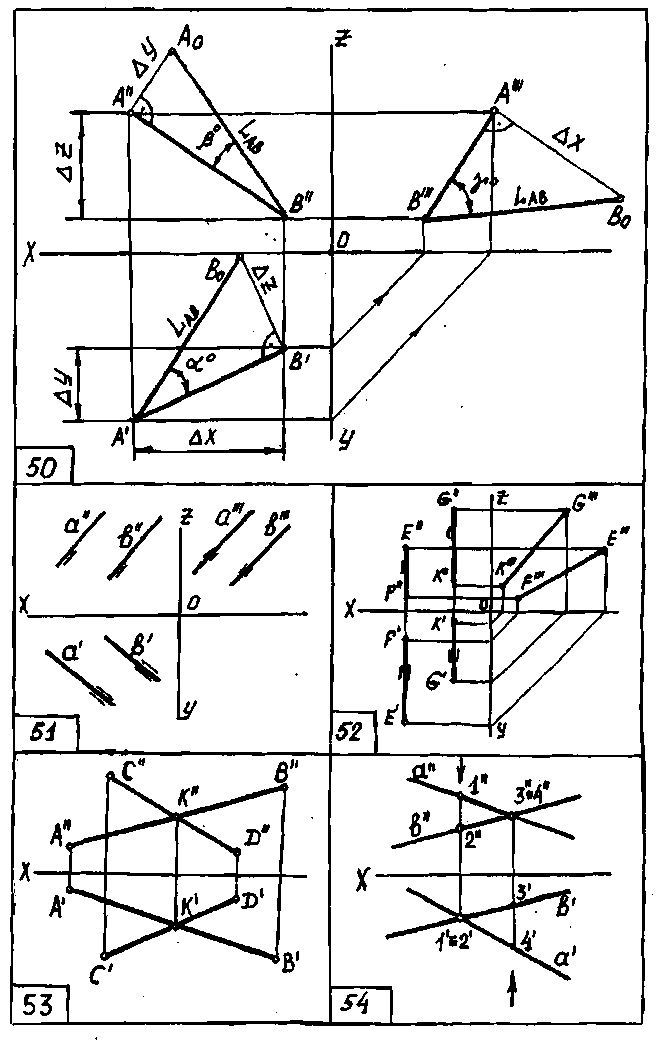
треугольника, катеты которого - профильная проекция отрезка А"'В'" ( чертеж не приводится ).

На чертеже 50 показан пример определения длины отрезка АВ и уг­лов наклона его к плоскостям проекций: \АВ\ - длина отрезка АВ; α° , β° , γ° - углы его наклона соответственно к π1, π_2, π_3.