4 Плоскость

4.1 Способы задания плоскости

На эпюре плоскость может быть задана графически одним из следующих способов:

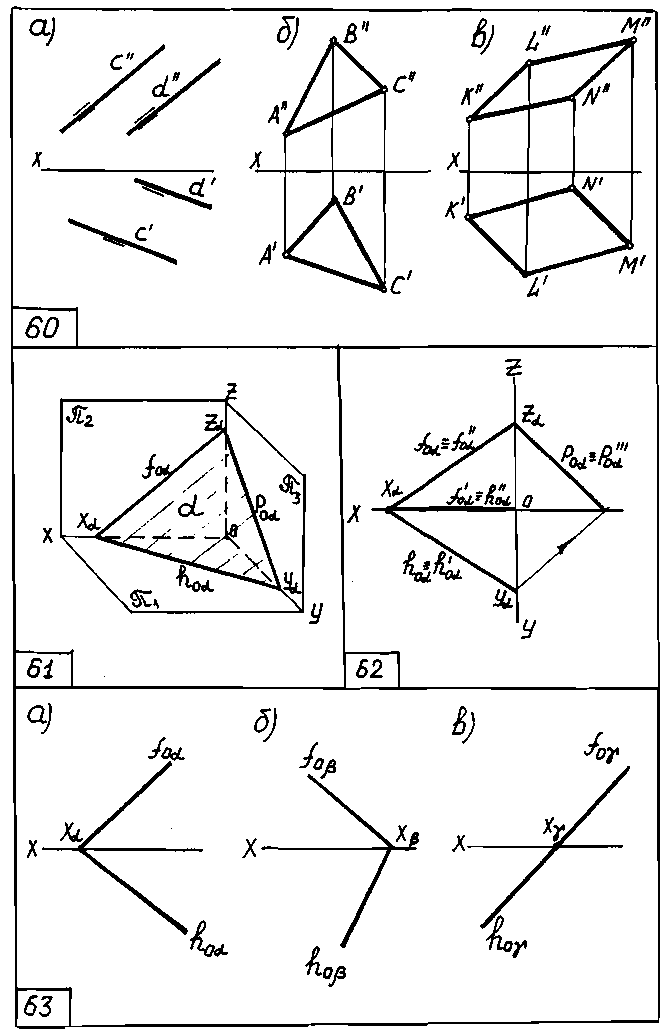
1) тремя точками, не лежащими на одной прямой (А, В, С – черт.59а);

2) прямой и точкой вне её ( прямая а и точка А – черт. 59б);

3) двумя пересекающимися прямыми (а и b – черт. 59в);

4) двумя параллельными прямыми (с и d – черт. 60а);

5)плоской фигурой (∆АВС и параллелограмм КLМN - черт. 60б и черт.60в).

Каждый из перечисленных способов задания плоскости легко может быть преобразован в другой.

Кроме того, плоскость на эпюре может быть задана следами. Следом плоскости α называется линия пересечения этой плоскости с плоскостью проекций. В системе трех плоскостей проекций π1, π_2, π₃ плоскость общего положения имеет три следа:

h_оа- горизонтальный след плоскости α;

foa - фронтальный след плоскости α;

pоа- профильный след плоскости α.

На месте пересечения плоскости α с осями получаем точки, на­зываемые точками схода следов: X_α; Y_α; Z_α.

Иногда плоскость может быть задана координатами точек схода следов. На черт. 62 приведён эпюр плоскости α , заданной следами в системе π1, π_2, π₃ .

В дальнейшем для упрощения записи следы плоскости могут обозначаться так, как показано на чертеже 63, т.е. только следами, а не

проекциями.

4.2 Положение плоскости в пространстве относительно плоскостей проекций

На чертежах 62, 63 изображены плоскости, которые не перпендикулярны ни к одной из плоскостей проекций. Это плоскости общего положения. Рассмотрим свойства проекций плоскостей частного положения на эпюре.

1. Плоскости, перпендикулярные плоскостям проекций – проецирующие плоскости:

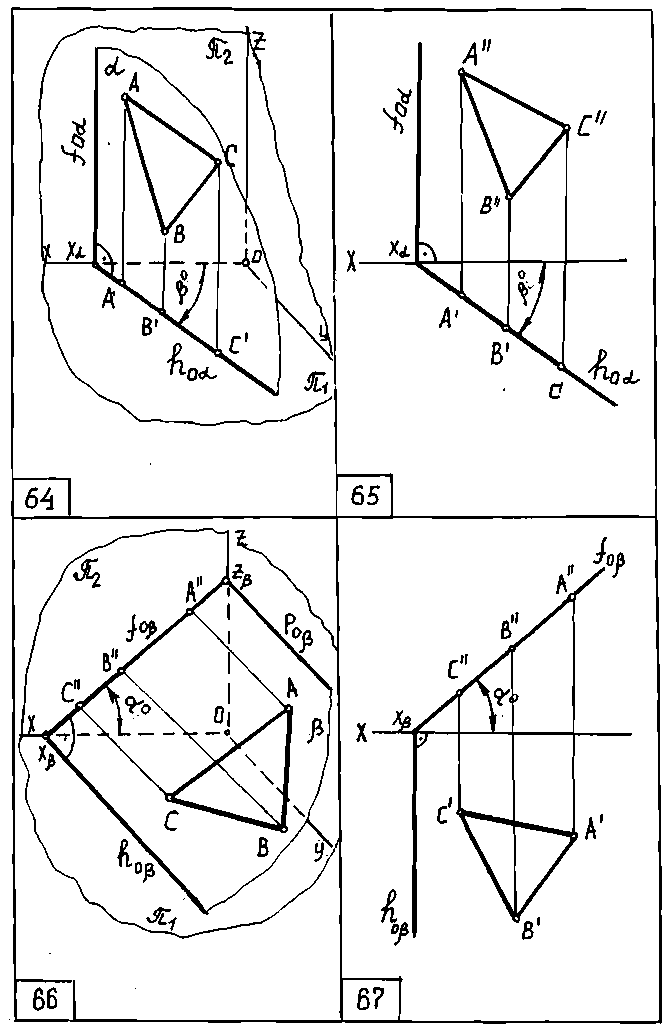
а) α перпендикулярна π1 - горизонтально проецирующая плоскость (черт. 64, 65) Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположенная в этой плоскости, проецируется на π1 в прямую линию, совпадающую с горизонтальным следом h_оа . Угол β° равен углу наклона плоскости α к плоскости проекций π_{2 .}Фронтальный след такой плоскости перпендикулярен к оси X..

б) β перпендикулярна π₂ - фронтально проецирующая плоскость (черт. 66, 67). Основным свойством фронтально проецирующей плоскости является то, что любая фигура, расположенная в той плоскости, проецируется на π₂ в прямую линию, совпадающую с фронтальным следом плоскости β . Угол α° равен углу наклона плоскости Р к горизонтальной плоскости проекций. След такой плоскости перпендикулярен к оси X.

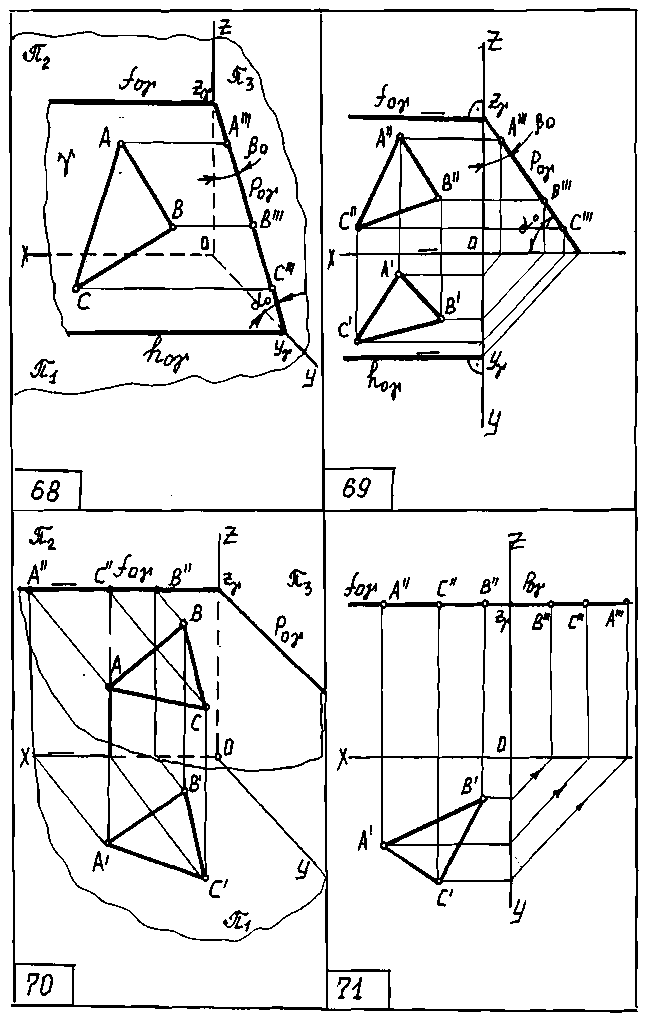
в) γ перпендикулярна π₃ - профильно проецирующая плоскость (черт. 68, 69). Проявляет те же свойства по отношению к π₃, что и две предыдущие плоскости.

2. Плоскости, параллельные плоскостям проекции -плоскости "уровня":

а) γ || π1 - горизонтальная плоскость (А'В'С' =АВС, черт. 70, 71).

б) δ|| π₂ - фронтальная плоскость. Свойства её проекций видны на чертежах 72,73.

в) η || π₃ - профильная плоскость. (Чертеж не приводится).

4.3 Проведение проецирующей плоскости через прямую линию

Приём проведения проецирующей плоскости через прямую ли­нию ("заключение" прямой в плоскость), является важным для решения довольно

большого числа позиционных задач.

Через прямую общего положения может быть проведена любая из проецирующих плоскостей. На чертежах 74, 75 через прямую общего положения АВ проведена горизонтально проецирующая плоскость. На чертежах 76, 77 прямая СD заключена во фронтально проецирующую плоскость β. Для проведения этого приёма используются свойства проецирующих плоскостей (см. п. 4.2).