Точка. Прямая. Плоскость

1 Метод проекций

Центральная проекция (коническая, полярная) - плоское изображение, полученное при помощи проецирующих лучей, проходящих через одну и ту же точку S, называемую центром проекций (черт.1).

Параллельная проекция - это изображение, полученное при по­мощи проецирующих лучей, параллельных какому-то заданному направлению (черт. 2).

Если направление проецирования (S) составляет с плоскостью проекций (π₁) прямой угол (S перпендикулярно π₁), то такая проекция называется прямоугольной (ортогональной).

Ортогональное проецирование является основным в черчении, т.к. обладает большей наглядностью. Более подробно об инвариантных свойствах центрального, параллельного и ортогонального проецирования можно узнать из учебников, приведенных в списке литературы.

Поскольку одна проекция точки, линии или фигуры на одну плоскость проекций не определяет ее положения в пространстве, необходимо иметь их проекции на две взаимно перпендикулярные плоскости проекций.

Параллельные прямоугольные проекции на две взаимно перпендикулярные неподвижные плоскости проекций - основной метод составления технических чертежей. Этот метод называется методом Монжа.

2 Точка

2. 1 Точка в системе двух плоскостей проекций π1, π2

Согласно методу Монжа возьмём две взаимно перпендикулярные плоскости и примем их за плоскости проекций (черт.3). Условимся их называть: π1 - горизонтальная плоскость проекций; π₂ - фронтальная плоскость проекций; X - ось проекций (пересечение π1, с π₂); π1/π₂ - система плоскостей проекций.

Плоскости π1 и π₂ делят пространство на четыре двугранных угла. Эти четыре пространства называются четвертями. Первой четвертью считается пространство, грани которого обозначены π1 и π₂.

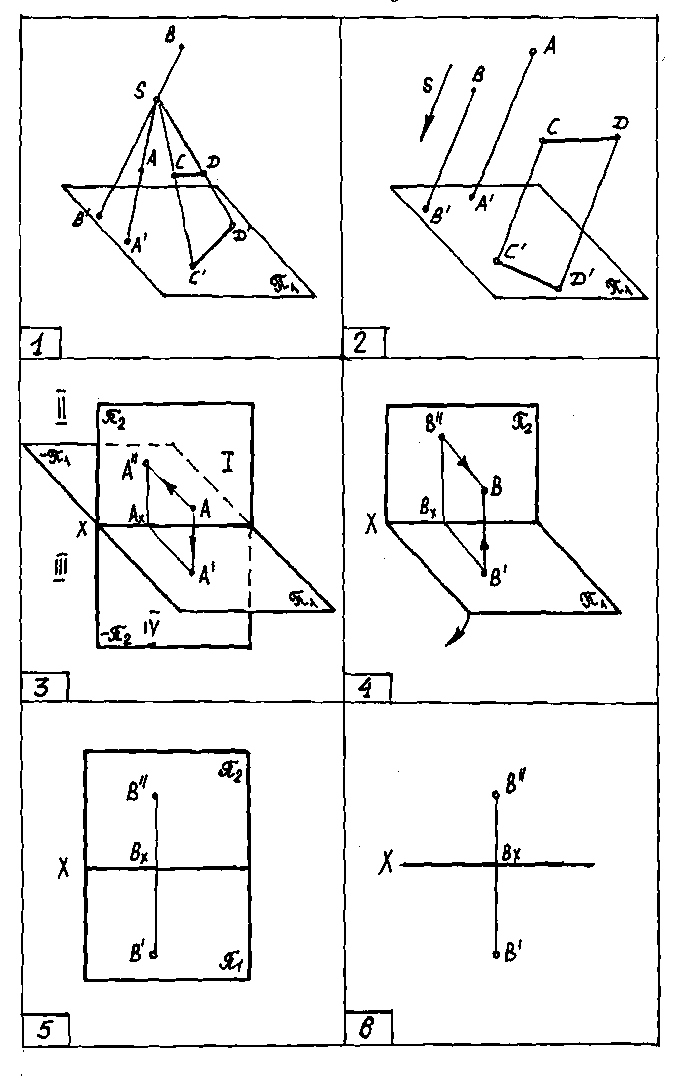
Прямая, перпендикулярная к оси проекций X, и соединяющая горизонтальную и фронтальную проекции точки называется линией связи .

Изображение, полученное в результате поворота плоскости проекций π1 на угол 90° до совмещения с π₂, называется эпюром. В дальнейшем эпюр мы будем представлять так, как показано на чертеже 6, поскольку плоскости проекций безграничны. По эпюру мы можем определить расстояния от точки В до плоскостей проекций:

А,А " - расстояние от точки А до плоскости π1;

А,А' - расстояние от точки А до плоскости π₂.

2.2 Точка в системе трёх плоскостей проекций

В систему плоскостей π1/π₂ введём ещё одну плоскость проекций π₃, перпендикулярную как к π1, так и к π₂ (черт. 7). π₃ -профильная плоскость проекций. Линии пересечения трёх плоскостей образуют координатные оси, пересекающиеся в точке О, которая является началом координат.

На чертеже 7 показано построение проекций точки А в системе трёх плоскостей т.е. на три плоскости проекций; опустив перпендикуляры на эти плоскости, получаем соответственно горизонтальную (А'), фронтальную (А") и профильную (А '") проекции точки А.

Перейдём к плоскому изображению, совместив плоскости π1 и π₃ с плоскостью π₂ поворотом каждой на 90°, как показано на чертеже 7 стрелками.

Получим эпюр точки А в системе трёх плоскостей проекций (черт. 8). При этом ось Y как бы раздвоилась - одна её часть ушла вниз с плоскостью π1, а вторая - вправо с плоскостью π₃ . Упростим плоское изображение как показано на чертеже 9 (поскольку плоскости проекций бесконечны в пространстве).

На эпюре горизонтальная (А') и фронтальная ( А") проекции точки А лежат на одной линии связи, которая перпендикулярна оси X; фронтальная (А") и профильная (А"') - на линии связи, перпендикулярной к оси Z; профильная проекция (А"') находится на таком же расстоянии от оси Z, как и горизонтальная (А') от оси X.

На полученном эпюре можно измерить удалённость точки А.

а) от π1: А_ХА" =А_УА'";

б)от π₂:А_хА'=А_гА'";

в) от π₃: А₂А " = ОА_Х =А_УА'.