4.6 Взаимное положение прямой линии и плоскости

Прямая может находиться в плоскости, быть параллельной ей или пересекать плоскость (о принадлежности прямой плоскости см. раздел 4.5).

Прямая а параллельна плоскости α, если она параллельна прямой b, принадлежащей этой плоскости. На чертеже 91 показаны прямые,

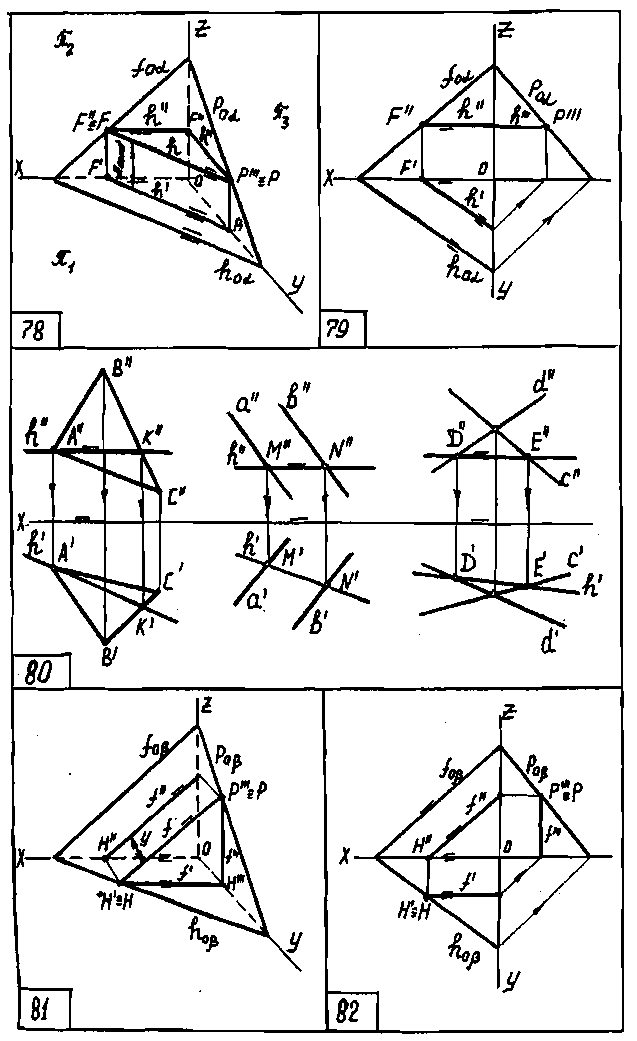
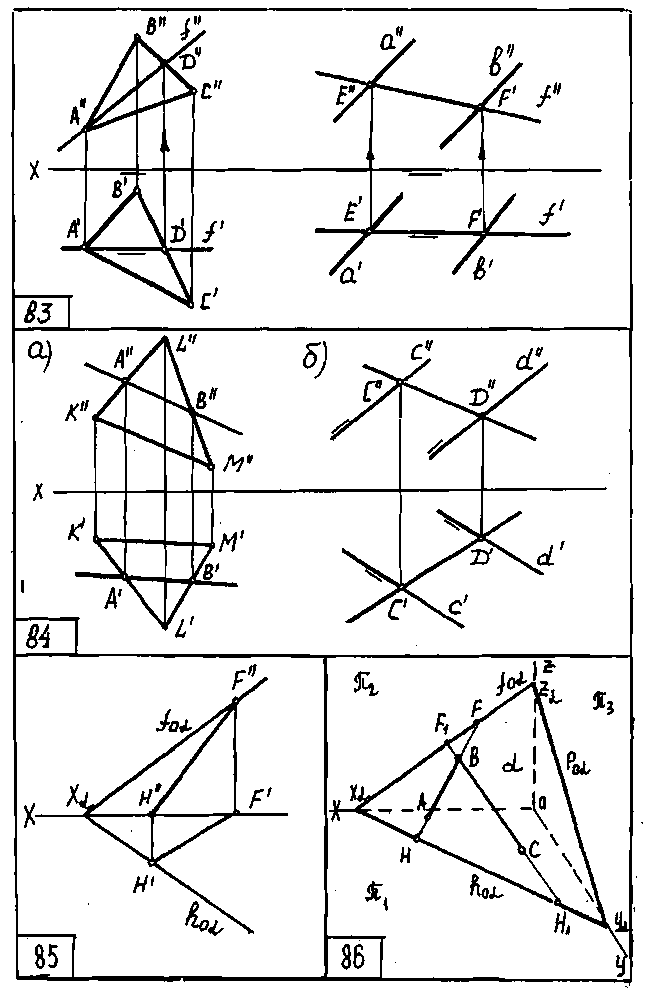
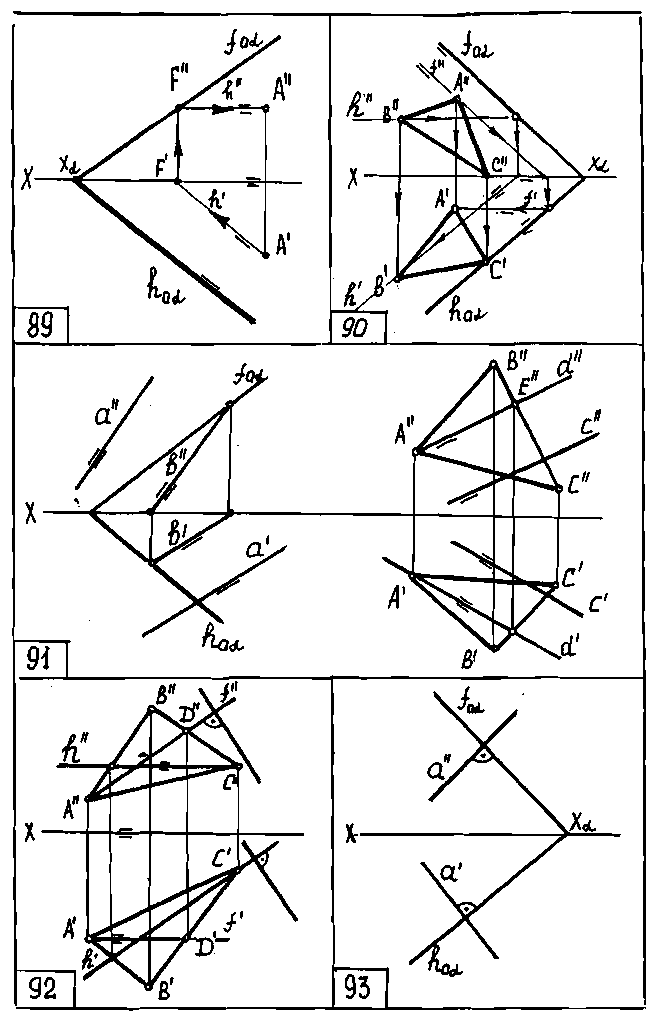
параллельные плоскостям, задан­ным следами и ∆АВС.

Прямая, пересекающая плоскость под углом 90°, т.е. перпендикулярная плоскости. Прямая а перпендикулярна плоскости α , если она перпендикулярна двум пересекающимся прямым b и c этой плоскости.

Если в плоскости α брать прямые а и b общего положения, то восстановить к ним перпендикуляр сложно, т. к. угол 90° искажается. Поэтому нужно брать такие прямые а и b, чтобы они были горизонталью (а = h) и фронталью (b = f) плоскости, тогда угол к ним проецируется без искажения (свойство проецирования плоских углов, см. п. 3.6).

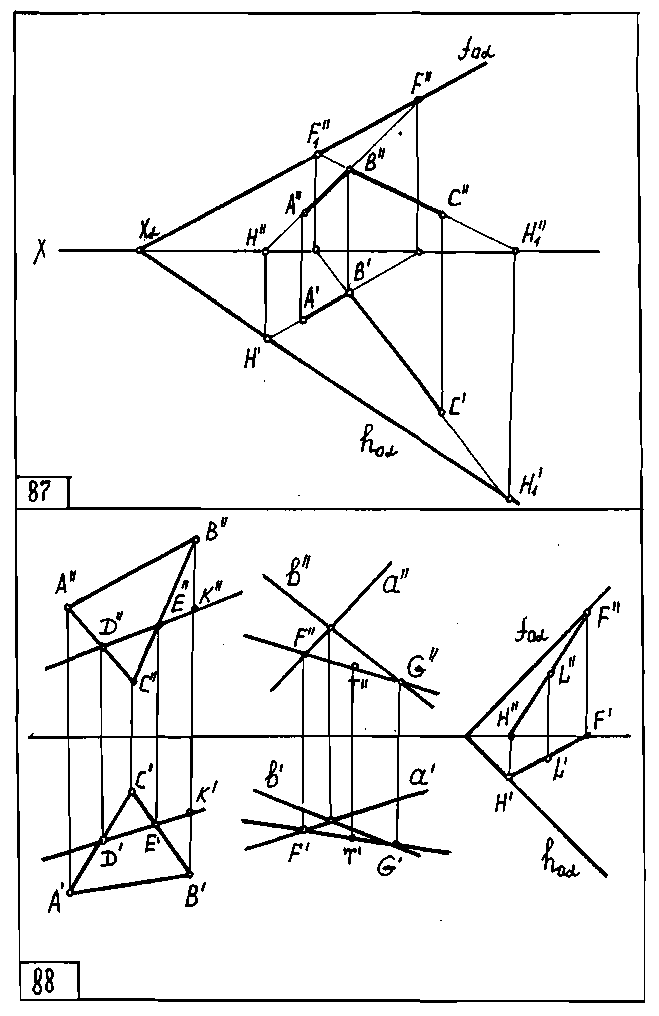
Итак, в плоскости, которую задаёт ∆АВС возьмём две пересе­кающиеся прямые h и f и проведём произвольную прямую а перпендикулярную плоскости α (∆АВС) при этом прямые углы между прямой а и прямыми f и h проецируются без искажения (черт. 92).

Следовательно, прямая а перпендикулярна плоскости α, если её проекции перпендикуляр­ны соответствующим проекциям горизонтали h и фронтали f этой плоскости.

Если плоскость задана следами (черт. 93), то горизонталью и фронталью плоскости являются её пересекающиеся следы. Следовательно, прямая а перпендикулярна плоскости α, если её проекции перпендикулярны соответствующим пересекающимся следам плоскости h_oa и f_oa.

4.7 Взаимное положение двух плоскостей

Две плоскости могут быть параллельными или пересекающимися.

Плоскости α и β параллельны, если две пересекающиеся прямые а и b одной плоскости параллельны двум пересекающимся прямым другой плоскости. На чертеже 94 показаны плоскости α || β.

Если плоскости заданы следами, то о взаимной параллельности их в пространстве можно судить по параллельности их одноимённых следов (следы

плоскости это те же пересекающиеся прямые). На чертежах 95, 96 изображённые плоскости параллельны. Однако, о параллельности профильно проецирующих плоскостей можно судить после построения их профильных следов (черт. 97).

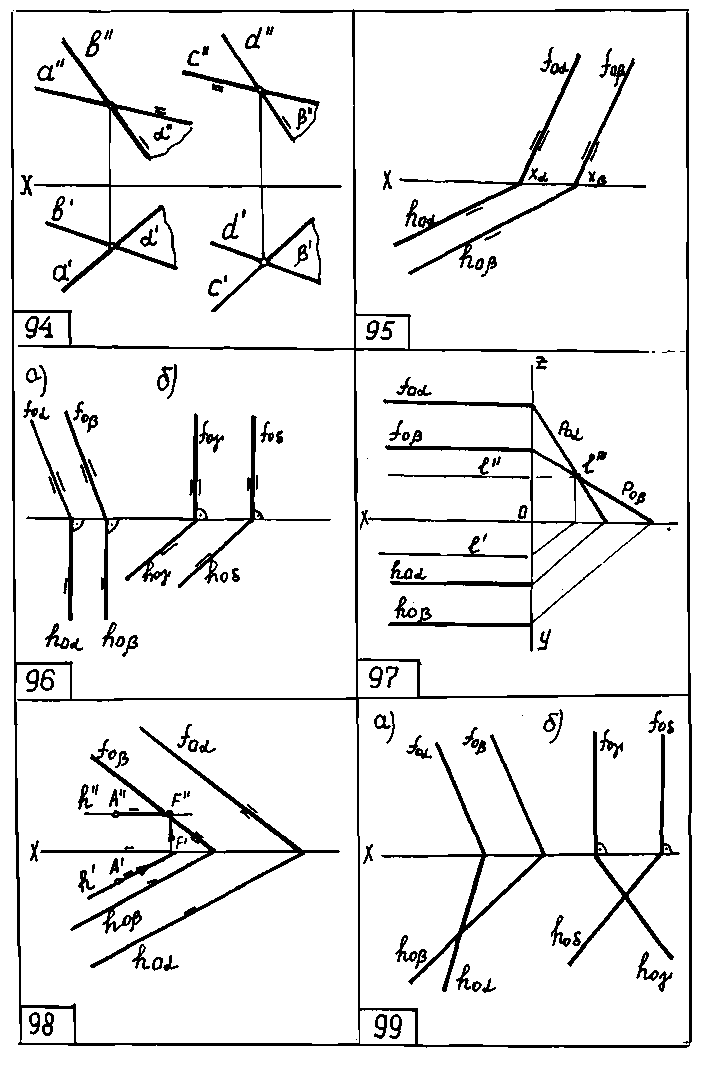
Пример: даны плоскость α и точка А, не принадлежащая этой

плоскости. Необходимо через точку А построить плоскость β, параллельную заданной плоскости α (черт. 98).

Пересекающиеся плоскости. Если у заданных плоскостей пересекается хотя бы одна пара следов, то эти плоскости пересека­ются (черт. 99а, б). Особый интерес представляют плоскости перпендикулярные, т. е. пересекающиеся под прямым углом.

Известно, что плоскости взаимно перпендикулярны, если в одной из них имеется прямая, перпендикулярная ко второй плоскости. Поэтому, плоскость перпендикулярную к заданной плоскости, можно построить через прямую, перпендикулярную заданной плоскости. На чертеже 100 дана прямая а перпендикулярная плоскости α следовательно, любая плоскость, проходящая через прямую а будет перпендикулярна плоскости α (на чертеже изображены две проецирующие плоскости β и γ и произвольная плоскость δ, следы которой проходят через следы прямой а.

Следует отметить: – у взаимно перпендикулярных плоскостей общего положения их одноимённые следы никогда не перпендикулярны; – если одна из заданных плоскостей (или обе, черт. 101) является плоскостью частного положения, то взаимная перпендикулярность на эпюре одной пары следов свидетельствует о перпендикулярности плоскостей в пространстве (положения приводятся без доказательств).