Глава II

Схема Бернулли

§1 Формула Бернулли

До сих пор мы изучали отдельные опыты и связанные с ними события, сейчас мы рассмотрим последовательности опытов или испытаний…

Испытание проводится nраз,

Мы будем считать, что выполнено несколько условий: 1) в каждом опыте может произойти или не произойти некоторое событие А с одной и той же вероятностью Р(обозначимq=1-P)

2) вероятность наступления или не наступления события А в i-ом опыте не зависит от наступления или не наступления события А в других опытах (в стом случае говорят, что испытание независимо)

В дальнейшем для краткости мы будем говорить, что испытания проводятся по схеме Б если выполняется два условия указанные выше.

Формула Бернулли

Пусть проводиться nиспытаний по схеме Бернулли и пустьP– вероятность наступления событияA(замечание: часто называемым успехом) и пустьq=1-P(вероятность неуспеха), тогда вероятность наступленияKуспехом приnиспытаниях, обозначаемая черездаётся равенством:

(1) , где,- формула Бернулли

Доказательство: Рассмотри и выпишем все возможные последовательности испытаний в которых ровно kуспехов и их вероятности

…

X– строк

Мы видим, что вероятность любой последовательности испытаний с kуспехами и(n -k)неуспехами равняется, т.к. в любой строчке содержитсяkбуквAи(n-k) букв.

Из комбинаторики известно, что (число сочетаний изnпоk), отсюда (*) получаем:

- доказано

Задача: известно, что вероятность выиграть по 1-ой облигации =0,1. Некто купил 6 облигаций. Найти вероятность того, что выиграют 2-е.

Решение: легко видеть, что выполнены условия схемы Бернулли:

1. вероятность выиграть по каждой облигации одинакова.

2. Вероятность выиграть по одной облигации не зависит от того, выиграли ли другие.

Тогда можно применить (1), надо найти , причёмР=0,1 , аq=0,9.

Ответ:.

Нам понадобятся два следствия из формулы Бернулли:

1. пусть проводится nиспытаний по формуле Бернулли и пусть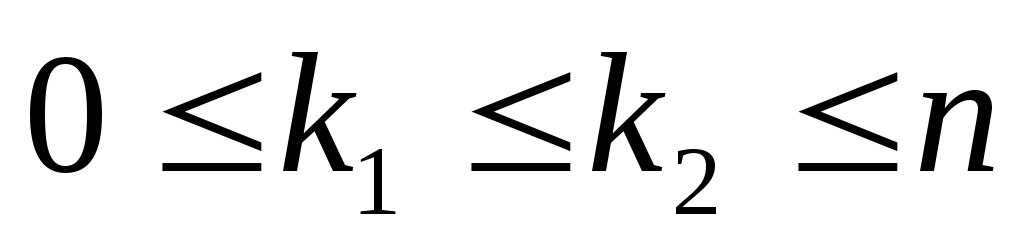, обозначим черезвероятность того, что число успехов будет не меньше, чемk1и не больше чемk2 при проведенииnиспытаний (т.е.)? Тогда справедливо равенство:

(2)

Доказательство:

Введём дополнительное событие D_i произошло ровноiуспехов приnиспытаниях

Ck₁k₂- число успехови

Тогда: (*)Ck₁k₂= D_k1 + D_k1+1 +…+D_k2Очевидно, что событияD_iD_j несовместны приi≠j , поэтому из (*) получаем:

(**)(вероятность суммы несовместимых событий равна сумме вероятностей)

По определению (***),

Из (***), (**) и (1) получаем (2).

Задача: В компьютерном классе 10 компьютеров. Известно, что с вероятностью 0,1 компьютер не исправен. Найти вероятность того, что на занятии будут исправны хотя бы 8 компьютеров

Решение

Мы видим, что выполняются условия схемы Бернулли

Р=0,9, q=0,1

По (2) находим:

Ответ:

Следствие 2: Во многих случаях необходимо найти вероятность хотя бы 1-го успеха при nиспытаниях, т.е.P_n(1,n), если использовать (2), то необходимо суммироватьnчисел, каждое из которых даётся (1), т.е. необходимо проводить довольно громоздкие вычисления, однако их можно измежать, используя более простую формулу.

Утверждение 2: Пусть проводиться nиспытаний по формуле Бернулли, тогда:

(3)

Доказательство:

Доказано

Задача: известно, что вероятность попасть при одном выстреле = 0,7, Пит стреляет 5 раз по одной цели. Найти вероятность её поражения.

Решение:

n=5,p=0,7,q=0,3P={(3)}=1-0,3⁵

Ответ:

Во многих, практически возможных задачах необходимо уметь оценивать число испытаний, гарантирующее хотя бы один успех, с наперёд заданной, большой вероятностью. Для этого применяется:

Пункт 2: Пусть проводятся испытания по схеме Бернулли с вероятность успеха при одном испытании pи пусть, тогда для того, чтобы вероятность хотя бы одного успеха была не меньше γ, число испытанийnдолжно удовлетворять неравенству:

(4)

Доказательство:

Пусть число испытаний nтаково, что вероятностьP{хотя бы один успех}≥γ. Из (3) получим, что вероятность 1-qⁿ≥γ=>1-γ=qⁿЛогарифмируем обе части:

ln(1-γ)≥n lnq,отсюда/

Отсюда и q=1-pполучаем (4).

Задача: известно, что одна ракета ПВО сбивает самолёт с вероятностью 0,6. Сколько надо выпустить ракет ПВО с разных установок чтобы вероятность сбить самолёт была не меньше 0,99.

Решение:

Необходимо найти вероятность хотя бы 1-го попадания при n-выстрелах. Известно:p=0,6,q=0,4,γ=0,99. Условия схемы Бернулли выполнены и воспользуемся (4).