2 Распределение Карла Пирсона

Рассмотрим случайную величину

(3) χ²= ξ₁²+ ξ₂²+ … + ξ_n², гдеξ N(0,1)

Она подчиняется хи- квадрат распределению с nстепенями свободы

Его плотность дается формулой:

(4)

можно показать, что

(5) M(χ_n²) =n;D(χ_n²) = 2n

График плотности:

Свойства случайной величин с симметричной (четной) плотностью распределения.

Пусть § - случайная величина с четной плотностью распределения

Пусть α= ½ иx_α иx_{1 - α} – квантили порядка α и (1 –α), тогда справедливо:

Утверждение!

(6) x_α= -x_{1 - α}

Доказательство: По свойству квантиля

Мы видим, что функция симметрична относительно оси координат, значит α₁=α₂и(6)доказано.

При больших объемах выборки приходится работать с распределением хи-квадрат при большом числе степеней свободы n. В этом случае необходимо использовать приближенные формулы.

Вообще для распределения Стьюдента и хи-квадрат напечатаны специальные таблицы, которые содержатся в учебнике по математической статистике, однако при больших nи необходимо использовать приближения. В случае распределения Стьюдента используютN(0,1), а распределения хи-квадрат приближают к нормальномуa=n,δ=смотри(5).

§3 Доверительные интервалы для генеральной средней нормального распределения

В этом параграфе мы рассмотрим следующую задачу:

Дана случайная величина ξ, подчиняющаяся нормальному распределению с параметрами а и δ, причем а = математическому ожиданию, или генеральному среднему не известен и требуется построить для него оценку в виде доверительного интервала по выборке x₁,x₂, ….,x_n.

Мы рассмотрим последние 2 случая:

1) параметр δизвестен

2) не известен

1) нам понадобится следующее:

Утверждение1!

(1)

подчиняется стандартному нормальному распределению или (ηN(0,1)) {стандартному нормальному распределениюM= 0D= 1}

Докажем только, что

(*)M_η= 0,D_η= 1

по формуле (1):

M(η) = (M() - 0) = {ДоказаноM(), не смещенное от центраM() =a} = {a-a} = 0

D(η) = {(1)} =D((-a)) = (D() +D(-a)) = {§2 утверждение 2} = δ²/n= 1

Построим, т.е. рассмотрим задачу построения доверительного интервала для a, при уровне доверия γ:

Определим:

(2)α = 1 - γ

Утверждение2!Пусть- квантиль порядкастандартного нормального распределения, тогда справедливо равенство:

(3)

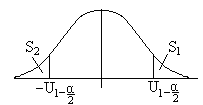
Доказательство: Вся площадь под кривой равна единице (свойство плотности) см. рисунок. По определению квантиля

(*)

следовательно: S₁= α / 2

В §2 доказано утверждение, что для симметричной плотности:

x_β= -x_{1 – β}(см 2.6))

в нашем случае =>

получили:

(**) S₂=α/ 2,S₁=α/2

Оценим вероятность

Построим доверительный интервал воспользовавшись (3):

Из (3)и(1)получаем:

помножим на минус, неравенства поменяют знак, и мы их поменяем местами

(4)

Отсюда мы получаем следующую

Теорема1: Пусть необходимо построить доверительный интервал при уровне доверия γ = 1 -α для неизвестного параметра а (равного генеральному среднему) по выборкеx₁,x₂, …,x_nи пусть- выборочное среднее,δ- известный параметр нормального распределения и- квантиль стандартного нормального распределения порядка, тогда интервал

(5)

будет искомым, т.е. доверительным.

Доказательство:сразу следует из равенства(4)и определения доверительного интервала 1.1.

Пример:известно, что точность теодолита (измеряемые углы) = 1, для того чтобы измерить угол с более высокой точностью провели измерения этим теодолитом 10 раз, а затем вычислили выборочное среднее= 34,2 требуется по этим данным построить доверительный интервал при уровне доверия 0,95 для величины измеряемого угла, учитывая, что точность прибора определяется величиной δ.

Решение:Дано γ = 0,95 =>α=0,05;= 34,2;δ= 1 (точность 1);n= 10;

По таблице стандартного нормального распределения находим: U_0,975≈ 1,96

получаем: (34,2 – 1,96 * ; 34,2 + 1,96 *)

или ≈ получаем: (33,6; 34,8) - это доверительный интервал для неизвестного угла при уровне доверия 0,95.