§2 Предельные теоремы.

Рассмотрим Марковскую цепь с состояниями S₁,S₂, …S_k

Если существует , причем этот предел не зависит отiи существует при любомj.

Если предельные вероятности существуют, то введем обозначение:

(1)

Физический смысл(аналогичен случаю непрерывногоt)

1) - это время, доля времени, которая цепь проводит вj-том состоянии.

2) - это вероятность застать систему вj-том состоянии, если мы посмотрим на нее в случайный далекий момент времени.

Исследуем вопрос о существовании предела вероятностей:

Теорема 1:(О существовании)

Пусть дана Марковская цепь с матрицей переходов P. Если при некоторомt₀все элементы матрицы строго >0, то предел вероятности существует.(Без доказательства)

Рассмотрим примеры, поясняющие, в каких случаях предел вероятности не существует.

1)

Видим, что существуют 0-ые элементы, поэтому найдем, P(2),P(3) в надежде, что она будет без нулевых элементов. При этом мы воспользуемсяТеоремой 1 из §1 (1.10) =>

2)

* - элемент > 0

Видим, что опять есть нулевые элементы.

3)

Вывод:При любомt,P(t) имеет вид (3) поэтомуТеоремао существовании не применима и возникает подозрение, что предел вероятности не существует.

Действительно мы видим, по матрице P, что если цепь находится в 1-оим или 2-ом состоянии, то она никогда не попадет в 3 или 4. Наоборот, если в начальный момент времени цепь находится в 3 - 4, то она не попадет в 1 или 2. Значит, для одних начальных состояний:

, т.е. предел зависит от начального состояния, поэтому предел вероятности не существует.

2)Рассмотрим цепь, задаваемую матрицей перехода:

Найдем P(2),P(3) и т. д. в надежде, что найдем матрицу без нулей и применимТеорему 1.

Видим, что:

P=P(3) =P(5) = … =

P(2) =P(4) =P(6) = … =,т.к.

P(4) =P²= (единичная)²

Очевидно, все P(t) содержат нули. Возникает подозрение, что предел вероятности не существует. Для этого, чтобы убедиться, рассмотрим траектории этой цепи:

Мы видим, что P₁₁(t) = {0,t– нечетное; 1,t- четное}

Значит: P₁₁(t): 1, 0, 1, 0 …

У этой последовательности limне существует.

Матрицы такого типа называются периодическими; в данном примере с периодом 2.

3)Дана цепь с матрицей переходов

Найдем P(2)

- по Теореме 1– предел вероятности существует

Рассмотрим вопрос о вычислении предела вероятностей.

Теорема 2: Пусть дана Марковская цепь с конечным числом состоянийk, у которой существует предел вероятности, тогда они могут быть найдены, как решение системы уравнений.

(4)

Доказательство: Мы знаем, что

Перейдем к lim

Пример.Используя пример с рыжими обычными женщинами, найдем долю рыжих женщин на этом острове через 1000 лет. Для этого найдем предел вероятности для цепи с матрицей

Очевидно, предел вероятности существует (потому что все элементы не 0).

Для их вычисления используем Теорему 2.

Запишем систему уравнений: (4)

=* 0,6 +* 0,2

=* 0,4 +* 0,8

+= 1

Выразим из 1-ого уравнения:

2==>=/ 2

/ 2 += 1 =>= 2/3,= 1/3

Следовательно, через 1000 лет на этом острове будет 1/3 рыжих и 2/3 обычных.

Пример 2.Марковская цепь задана матрицей перехода:

Надо определить существование пределов вероятности и их вычислить.

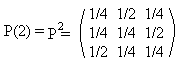
=> предел вероятности существует. Найдем их, используя Теорему 2:

=* ½ +* ½

=* ½ +* ½

=* ½ +* ½

++= 1

Легко видеть, что === 1/3. Это и есть предельная вероятность.

Пример.Система задана матрицей:

Находим P(2)

P²=P=>P^t=Pпри любомt

Следовательно, теорема 1не применима и возникает подозрение, что предел вероятности не существует.

Вероятность не существует, так же как и в первом примере, поведение системы зависит от начальных состояний.