
- •Предисловие
- •Глава 1. Исходные положения
- •Глава 2. Первая аксиома метрологии
- •2.1. Априорная информация
- •2.2. Источники априорной информации
- •2.2.1. Опыт предшествовавших измерений
- •2.2.2. Классы точности средств измерений
- •2.2.3. Условия измерений
- •Глава 3. Вторая аксиома метрологии
- •3.1. Способ получения измерительной информации
- •3.2. Измерительные шкалы
- •3.2.1. Шкала порядка
- •3.2.2. Шкала интервалов
- •3.2.3. Шкала отношений
- •Глава 4. Третья аксиома метрологии
- •4.1. Факторы, влияющие на результат измерения
- •4.2. Результат измерения
- •4.3. Формы представления результата измерения
- •4.3.1. Результат измерения по шкале порядка
- •4.3.2. Результат измерения по градуированным шкалам
- •4.4. Обратная задача теории измерений
- •4.5. Математические действия с результатами измерений
- •4.5.1. Математические действия с одним результатом измерения
- •4.5.2. Математические действия с несколькими результатами измерений
- •4.5.3. Приближенные вычисления
- •4.5.4. Решение систем уравнений, содержащих результаты измерений
- •Глава 5. Однократное измерение
- •5.2. Однократное измерение по градуированным шкалам
- •Глава 6. Многократное измерение
- •6.2. Многократное измерение по градуированным шкалам
- •6.2.1. Многократное измерение с равноточными значениями отсчета
- •6.2.2. Многократное измерение с неравноточными значениями отсчета
- •6.2.3. Обработка нескольких серий измерений
- •Глава 7. Качество измерений
- •7.1. Качество измерений по шкале порядка
- •7.2. Качество измерений по градуированным шкалам
- •7.3. Измерительная информация
- •Библиографический список
- •Предметный указатель

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
Г л а в а 7
КАЧЕСТВО ИЗМЕРЕНИЙ
7.1. КАЧЕСТВО ИЗМЕРЕНИЙ ПО ШКАЛЕ ПОРЯДКА
Результатом измерения по шкале порядка является решение. В соответствии с третьей аксиомой метрологии оно случайное, т.е. может быть правильным или неправильным. Таким образом, само собой разумеющимся показателем качества результата измерения по шкале порядка служит вероятность того, что он является правильным.
Не менее часто встречающимся на практике показателем качества решения является вероятность того, что оно является ошибочным. Чем больше вероятность ошибки, тем ниже качество результата измерения.
Ошибочные решения при измерении по шкале порядка подразделяются на ошибки I-го и II-го рода. Уменьшение вероятности ошибки I-го рода PI влечет за собой увеличение вероятности ошибки II-го рода PII , и наоборот. Так что вполне естественное стремление к минимизации ошибок является противоречивым.
Решения, наилучшим образом удовлетворяющие противоречивым требованиям, называются оптимальными. Объективно наилучшими (оптимальными) решениями были бы такие, при которых наблюдатель (оператор, контролер) вообще не совершал бы ошибок или, по крайней мере, вероятность их была бы минимальной. Поэтому критерий оптимизации
Рош = PI + PII = min
называется критерием идеального наблюдателя.
Вероятность ошибки I-го рода по правилу умножения вероятностей равна условной вероятности, умноженной на вероятность выполнения условия. В теории индикатора (см. п. 5.1) PI = αPc ; если речь идет о взаимоотношениях между поставщиком (производителем) и заказчиком (потребителем), - см. п. 6.1, - то PI = αРг . Соответственно, PII = βРсп или PII = βРб . При заключении контракта на поставку продукции, например, поставщик (производитель) заинтересован в том, чтобы вероятность ошибки I- го рода, состоящей в том, что годное изделие по ошибке будет забраковано, была бы как можно меньше. В материальном выражении риск поставщика составляет
Rп = g1PI = g1αРг ,
164
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
где g1 – цена ошибки I-го рода. В свою очередь риск заказчика, заинтересованного в том, чтобы вероятность пропуска брака из-за ошибки II рода была минимальной,
Rз = g2 βРб ,
где g2 – цена ошибки II-го рода. Объективно наилучшим (оптимальным) решением будет такое, при котором материальные потери от ошибок как I-го, так и II-го рода будут в среднем минимальными. Поэтому критерий оптимизации
R = Rп + Rз = g1αРг + g2 βРб = min
называется критерием минимума среднего риска. Критерий идеального наблюдателя
Рош = PI + PII = αРг + βРб = min
является частным случаем этого критерия.
По аналогии с формулами (25), (26) условные вероятности ошибок I-го и II-го
рода
α = ∞∫pг (Q)d Q ,
Qп
Qп
β = ∫pб (Q)d Q ,
−∞
где pг(Q) – плотность вероятности результата измерения контролируемого размера у годного изделия, pб(Q) – у бракованного, а Qп – некоторое пороговое значение результата измерения, на основании сравнения с которым принимается решение. Подставив эти выражения в формулу для среднего риска, получим:
∞ |
Qп |
R = ∫g1Pгpг (Q)dQ + ∫g2Pбpб(Q)d(Q). |
|
Qп |
−∞ |
Qп
Если теперь в правую часть этого уравнения добавить и вычесть ∫g1Pгрг (Q)dQ , то ра-
−∞
венство не нарушится, а формула для среднего риска примет вид:
Qп
R = g1Pг + ∫[g2Рбрб(Q)−g1Ргрг (Q)]d Q .
−∞
Средний риск будет минимальным при таком значении Qп, при котором производная от этого выражения по верхнему пределу равна нулю. Последняя в свою очередь равна подынтегральной функции при значении переменной, равном верхнему пределу. Таким
165

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
образом, условие минимума среднего риска записывается в виде:
[g2Рбрб (Qп )− g1Ргрг (Qп )]dQп = 0 ,
или |
|
|
|
||
|
рб(Qп ) |
= |
g1Рг |
||
|
|
|
|
. |
|
|
рг (Qп ) |
g2Рб |
|||
Плотности вероятности рг(Qп) и рб(Qп) называют иногда функциями правдоподобия. Каждая из них характеризует, насколько правдоподобно отнесение изделия к
числу годных или к числу бракованных. Но лучшей мерой правдоподобия является p (Q )
б( п) , обозначаемое буквой Λ и называемое отношением
рг Qп
правдоподобия. Пороговое значение Qп результата измерения контролируемого размера, синтезированное по критерию минимума среднего риска:
Λ = g1Рг , g2Рб
обеспечивает объективно наилучшее (оптимальное) решение, гарантирующее, что материальные потери от ошибок I-го и II-го рода будут в среднем минимальными, если решение принимается по правилу:
при Q ≤ Qп изделие признается годным; при Q > Qп изделие бракуется.
Пример 59. Используя условия примера 51, синтезировать решение, оптимальное по критерию минимума среднего риска, если объект бракуется уже при отношении мощности сигнала к мощности
шумовых помех u 2 = 5 . Репутация фирмы-поставщика такова, что вероятность брака на порядок меньше
σu2
вероятности того, что объект окажется годным, но ошибка II-го рода обходится в 100 раз дороже ошибки I-го рода.
Решение. 1. Отношение правдоподобия
|
|
|
|
(U− |
|
)2 |
|
U2 |
|
|
|
2 U |
|
1 |
|
|
U |
|
1 |
|||||||
|
p (U) |
− |
u |
+ |
|
u |
− |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
− |
|
|
|||||
|
2σ2 |
2σ2 |
|
σ2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
u |
|
2 |
|
|
u 2 . |
||||||||||||||||
Λ = |
б |
|
= e |
|
u |
|
u |
= e |
|
|
u |
|
|
|
|
|
|
|
= e |
|||||||
рг (U) |
|
|
|
|
|
|
|
|
||||||||||||||||||
2. Средний риск будет минимальным, если
|
U |
− |
1 |
|
|
g1Pг |
|
|
1 |
|
||||
5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
= |
= |
10 = 0,1. |
||||||||
e |
|
|
u |
|
|
|
||||||||
|
|
|
|
|
|
100 |
||||||||
|
|
|
|
|
|
|
|
|
g |
P |
|
|
||
|
|
|
|
|
|
|
|
|
|
2 б |
|
|
|
|
3. Прологарифмировав левую и правую части этого уравнения, получим:
166
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
U |
− |
1 |
|
= −2,3 , |
|
5 |
|
|
|||
|
u |
|
2 |
|
|
или, учитывая, что u = σu  5 = 5 2,25 = 3,35 B ,
5 = 5 2,25 = 3,35 B ,
U ≈ 0,1 В.
4. Материальные потери от ошибок I-го и II-го рода будут в среднем минимальными, если правило принятия решение будет следующим:
при u ≤ 0,1 В объект принимается; при u > 0,1 В объект бракуется.
Весьма важным является вопрос о синтезе оптимального решения при том или ином дефиците априорной информации. Рассмотрим несколько таких случаев.
I. Если неизвестна цена ошибок g1 и g2 , то применяется критерий идеального наблюдателя.
Пример 60. По условиям предыдущего примера синтезировать решение, оптимальное по критерию идеального наблюдателя:
Рош = РI + РII = αРг + βРб = min .
Решение. При синтезе решения по критерию идеального наблюдателя
Λ= Рг .
Рб
Отсюда
|
U |
− |
1 |
|
|
Pг |
|
|
5 |
|
|
|
|
|
|||
|
|
|
|
|||||
e |
u |
|
2 |
|
= |
=10 . |
||
|
|
P |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
После логарифмирования получим:
U |
− |
1 |
|
= 2,3 , |
|
5 |
|
|
|||
|
u |
|
2 |
|
|
или, учитывая, что u = 3,35 B ,
U ≈ 3,2 В.
Вероятность ошибок в среднем будет минимальной, если решение принимать по правилу:
при u ≤ 3,2 В объект принимается; при u > 3,2 В объект бракуется.
167
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
II. Если неизвестны априорные вероятности Рг и Рб , то может оказаться целесообразным использование минимаксного критерия. Идея заключается в том, чтобы минимизировать максимально возможный риск, откуда и происходит название критерия.
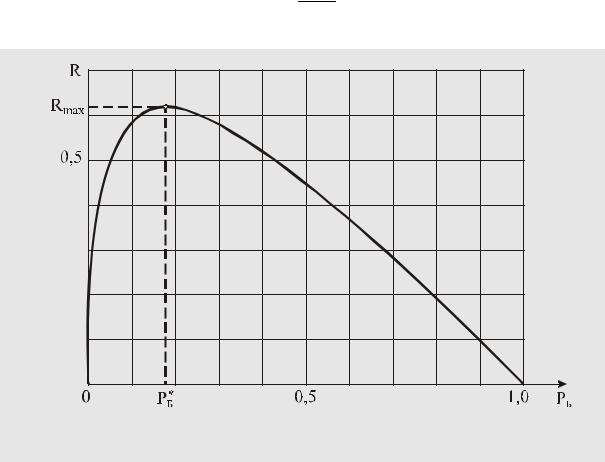
Дело в том, что средний риск должен стремиться к нулю как при Рб → 0 (что равносильно Рг → 1), так и при Рб → 1 (что равносильно Рг → 0), ибо если одна из априорных вероятностей равна единице, а другая нулю, то налицо полная определенность, и никакого риска совершить ошибку, принимая решение, нет. Следовательно, средний риск имеет максимальное значение при некотором значении Рб* = 1 - Рг*, не равном ни нулю, ни единице (см. рис. 78). Если обозначить это максимальное значение как Rmax , а соответствующее ему отношение правдоподобия как
Λ = g1Рг ,
g2Рб
Рис. 78.
Зависимость среднего риска от априорной вероятности Рб в примере 61
то на практике средний риск при любом Рб , отличном от Рб*, будет меньше Rmax , соответствующего Λ*. Таким образом, решающее правило, основанное на использовании отношения правдоподобия Λ*, будет ориентировано на наихудший случай и будет оптимальным (наилучшим) решением в этом наихудшем случае.
Если бы как-то удалось узнать, чему равна вероятность Рб или Рг , то средний риск можно было бы сразу уменьшить. Но минимаксный критерий как раз и применяется именно тогда, когда эти априорные вероятности неизвестны.
168

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
Пример 61. Используя условия примеров 51 и 59, синтезировать решение, оптимальное по минимаксному критерию.
Решение. 1.Используя интегральные представления для условных вероятностей ошибок I-го и II-го рода, можно получить следующее выражение для среднего риска:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
U |
|
|
|
1 |
|
|
U |
|
|
|
|
u |
|
|
|
|
|
|||||||||||||||||||||||||
|
R = g1Pг |
|
|
|
|
|
+ g2Pб |
|
|
|
|
|
− |
|
|
|
= |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
− L |
σ |
|
|
|
2 |
+ L |
σ |
|
|
|
σ |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
1 |
|
|
U |
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|||||||||||||||||||||
|
(1− Pб ) |
− L |
|
|
|
|
|
|
+ g2Pб |
1 |
|
|
|
|
U |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
= g1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ L |
|
|
|
|
−1 |
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
u |
|
|
σu2 |
|
|
|
|
2 |
|
|
|
u |
|
|
|
|
|
σu2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По этой формуле с учетом того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
U |
− |
1 |
= 1 |
|
1− Pб , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
e |
u |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
= |
|
1 + 1 ln |
|
1− Pб |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
5 |
100 P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
построена зависимость R от Pб на рис. 78. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.Средний риск достигает значения Rmax = 0,61 |
|
при Pб = P = 0,174. Исходя из этого, |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Λ = g1 (1− Pб )= 0,047 . g2 Рб
Соответствующий такому отношению правдоподобия порог находится из уравнения:
5 U − 1
e u 2 = 0,047 .
После логарифмирования и необходимых преобразований получаем:
U* = - 0,11 u .
3. Правило принятия решения, оптимального по минимаксному критерию, записывается следующим образом:
при u ≤ - 0,37 В объект принимается; при u > - 0,37 В объект бракуется.
III. Если неизвестно отклонение контролируемого размера от номинала, приводящее к браку, или величина сигнала, который должен обнаруживаться индикатором, т.е. если неизвестна β, то наилучшим (оптимальным) решением будет такое, которое обеспечивает заданную условную вероятность ошибки I-го рода α. Такой критерий оп
169
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
тимизации называется критерием Неймана-Пирсона. Иллюстрацией применения этого критерия служат примеры 52 и 53.
IV. Если под влиянием внешних факторов меняется мощность шумовых помех σu2 (см. пример 52), то приходится создавать сложные технические системы со следя-
щим порогом. В этих условиях может найти применение решающее правило, при котором порог обнаружения не зависит от мощности нормальных шумовых помех. Это рав-
носильно отсутствию априорной информации о σu2 .
Воспользуемся приемом, показанным на рис. 75, и за время, в течение которого изменением σ2X
можно пренебречь, образуем из экспериментальных данных две серии по m и n независимых значений показания X. Совместим начало координат со средним значением показания в каждой серии X1 = X 2 = X . Тогда случайные величины
n |
2 |
m |
2 |
||
y1 = ∑(X i − |
|
) ; |
y2 = ∑(X j − |
|
) |
X |
X |
||||
i =1 |
|
|
j=1 |
|
|
будут подчиняться χ – распределению модуля многомерного нормального вектора, выражение для плотности вероятности которого приведено в табл. 8.
Образуем некоторую, пока неизвестную, функцию z = f (y1, y2) . Плотность вероятности этой функции двух независимых положительных случайных величин определяется по формуле:
p(z)= ∞∫∫∞ p(y1 )p(y2 )δ[z −f (y1, y2 )]d y1 d y2 ,
0 0
где δ – дельта-функция. Отсюда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
∞ ∞ |
|
|
|
− |
y 12 + y 22 |
|
|
||||||
|
|
|
p (z )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ∫ y1n −1 y 2m −1 e |
|
|
2 σ |
2 |
|
δ [z − f (y1 , y 2 )]d y1 d y 2 , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
||||||||||||||||||||
|
|
|
|
2 |
|
m + n |
|
|
m |
|
|
n |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
(2 σ X |
) |
2 |
Γ |
|
|
|
Γ |
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
m |
и |
n |
|
– гамма-функции. Подстановкой |
y |
|
= t ; |
|
|
y |
2 |
|
|
= t |
|
последнее выражение приводится к |
||||||||||||||||||||||||
Γ |
|
|
Γ |
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
1 |
|
|
σX |
|
|
|
|
2 |
|
||||
виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (z )= |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
∞ ∞ |
|
e − |
|
t12 +t22 |
δ [z − f (σ X t1 , σ X t 2 )]d t1 d t 2 , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ∫ |
t1n −1t 2m −1 |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
m + n |
m |
|
|
|
n |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
Γ |
|
|
Γ |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где зависимость p(z) от σX входит только через функцию f (σX t1, σX t2) . Соответствующим выбором этой функции такую зависимость можно исключить.
Хотя теоретический интерес представляет отыскание и исследование всего многообразия функций, удовлетворяющих сформулированному требованию, ограничимся простейшей:
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
σX |
t2 |
|
k |
|
|
k |
|||
|
|
|
|
t2 |
|||||||
f (σX t1 |
, σX t2 )= |
|
|
|
|
= |
|
. |
|||
σ |
|
t |
|
1 |
|
||||||
|
|
|
X |
1 |
|
|
t k |
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
170

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив |
t |
2k |
|
=ϑ , заменив в подынтегральном выражении t |
2 |
на t |
ϑ |
k , при d t |
2 |
= t kϑk −1 dϑ полу- |
||||||||||||||||||||||||
1 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
||||||
|
t |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p (z )= |
|
|
4 k |
|
|
|
|
|
|
|
∞ ∞ |
|
|
|
|
|
|
|
− |
1 +ϑ |
2 k |
t12 |
δ (z − ϑ )d t1 d ϑ . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m + n |
−1 km −1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫ ∫t1 |
|
|
|
ϑ |
e |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
m + n |
m |
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
2 |
Γ |
|
|
|
Γ |
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя свойство δ-функции, при z =ϑ найдем, что |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 k z km −1 |
|
|
|
|
|
∞ |
|
|
|
|
1 + z |
2 k |
|
|
|||||||||
|
|
|
|
|
|
p (z )= |
|
|
|
|
|
|
|
m + n −1 |
|
− |
|
|
|
|
t12 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫t1 |
|
|
e |
|
|
|
|
|
d t1 . |
|
|
||||||||
|
|
|
|
|
|
|
m + n |
|
|
|
m n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
Γ |
|
|
Γ |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подстановкой t12 =ξ последний интеграл приводится к табличному. Окончательно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(z)= |
|
|
|
|
|
|
2 k |
|
|
|
|
|
|
|
|
|
zkm−1 |
|
|
|
|
, |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
|
|
|
|
2k |
m+n |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Β |
|
2 |
|
, |
|
2 |
|
|
|
(1 + z ) |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
m |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m |
|
n |
|
|
Γ |
|
Γ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
– бета-функция. Этот результат под названием z-распределение включен в |
|||||||||||||||||||||||||||||||||||||||||
где Β |
|
, |
|
|
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
m+ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Γ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
табл.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как p(z) не зависит от σ2X , то и условная вероятность ошибки I-го рода не зависит от мощно- |
||||||||||||||||||||||||||||||||||||||||||||||
сти нормальных шумовых помех: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
p(z)d z = |
|
|
|
|
|
|
2 k |
|
|
|
|
∞ |
|
z km−1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
α = |
∫ |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
d z . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
|
|
|
|
2 k |
|
m+n |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
zп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
+ z |
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Β |
|
|
|
|
|
|
zп |
|
|
|
|
|
|
|
|
|||||||||||
Интеграл здесь с помощью подстановки |
|
|
|
|
1 |
|
|
|
|
|
=ς |
|
выражается через неполную бета-функцию |
||||||||||||||||||||||||||||||||||
1+ z2k |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζп |
|
|
n |
|
|
|
|
|
|
m |
−1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
|
|
|
|
−1 |
(1 −ζ ) |
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Β |
, |
|
|
= |
|
∫ |
ζ 2 |
|
|
|
|
dζ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζп |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с верхним пределом ζп = |
|
1 |
. |
Вводя в рассмотрение отношение неполной бета-функции |
|||||||||||||||||||||||||||||||||||||||||||
1+ zп2 k |
|||||||||||||||||||||||||||||||||||||||||||||||
I |
m |
, |
n |
|
= |
|
|
2 |
2 |
|
|||
|
ζп |
|
|
|
||
Β |
|
m |
, |
n |
|
|
||||||
ζп |
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
||||||||
|
2 |
|
|
|
|
, |
||||||
|
m |
|
|
n |
|
|||||||
|
|
|
|
|
||||||||
Β |
|
|
|
, |
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
||||||
получим следующее выражение для определения порога обнаружения
1
zп = 1 −ζпζп 2 k
по заданной условной вероятности ошибки I-го рода: |
|
|
|
|
||
|
m |
|
n |
|
||
α =Iζ |
|
|
, |
|
. |
|
2 |
2 |
|||||
|
п |
|
|
|||
171
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
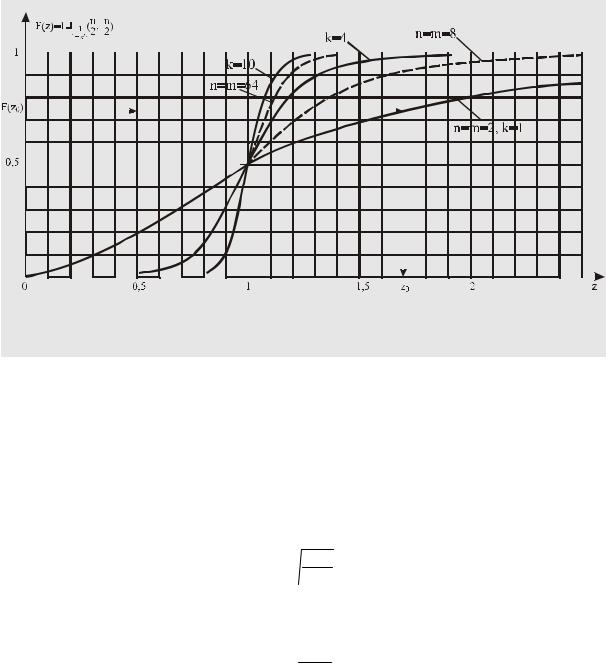
По табличным значениям неполной бета-функции на рис. 79 , для примера, построены графики интегральной функции распределения вероятности
|
|
|
|
|
|
|
|
|
|
|
m |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(z)=1−Iζ |
2 |
, |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 79.
Интегральные функции распределения вероятности F(z)
при нескольких значениях k и m = n. Задавшись значением |
|
|
|
||
F(zп )=1 − α =1 − Iζ |
m |
|
n |
|
|
|
|
, |
|
, |
|
|
2 |
||||
|
п 2 |
|
|
||
можно по графику на рис. 79 найти пороговое значение zп , которое не зависит от мощности нормальных помех.
На линейной шкале отсчетного устройства z подчиняется z-распределению вероятности с k = 1, а
zп =  1−ζпζп .
1−ζпζп .
На квадратичной шкале z2 подчиняется z-распределению вероятности с k = 12 (распределению Р.А. Фишера в табл. 8), а
z2 = 1−ζп .
п ζп
На логарифмической шкале плотность вероятности
p(ln z)= |
2 |
|
|
|
|
|
|
emln z |
|
|
; |
|||||
m |
|
n |
|
|
|
|
|
2ln z |
|
m+n |
||||||
|
|
|
(1+ e |
) |
|
|
|
|||||||||
|
Β |
|
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F(ln z)= |
1− Iζ |
m |
|
n |
|
|
|
|
|
|||||||
|
|
, |
|
|
, |
|
|
|
|
|||||||
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
172
