
- •Предисловие
- •Глава 1. Исходные положения
- •Глава 2. Первая аксиома метрологии
- •2.1. Априорная информация
- •2.2. Источники априорной информации
- •2.2.1. Опыт предшествовавших измерений
- •2.2.2. Классы точности средств измерений
- •2.2.3. Условия измерений
- •Глава 3. Вторая аксиома метрологии
- •3.1. Способ получения измерительной информации
- •3.2. Измерительные шкалы
- •3.2.1. Шкала порядка
- •3.2.2. Шкала интервалов
- •3.2.3. Шкала отношений
- •Глава 4. Третья аксиома метрологии
- •4.1. Факторы, влияющие на результат измерения
- •4.2. Результат измерения
- •4.3. Формы представления результата измерения
- •4.3.1. Результат измерения по шкале порядка
- •4.3.2. Результат измерения по градуированным шкалам
- •4.4. Обратная задача теории измерений
- •4.5. Математические действия с результатами измерений
- •4.5.1. Математические действия с одним результатом измерения
- •4.5.2. Математические действия с несколькими результатами измерений
- •4.5.3. Приближенные вычисления
- •4.5.4. Решение систем уравнений, содержащих результаты измерений
- •Глава 5. Однократное измерение
- •5.2. Однократное измерение по градуированным шкалам
- •Глава 6. Многократное измерение
- •6.2. Многократное измерение по градуированным шкалам
- •6.2.1. Многократное измерение с равноточными значениями отсчета
- •6.2.2. Многократное измерение с неравноточными значениями отсчета
- •6.2.3. Обработка нескольких серий измерений
- •Глава 7. Качество измерений
- •7.1. Качество измерений по шкале порядка
- •7.2. Качество измерений по градуированным шкалам
- •7.3. Измерительная информация
- •Библиографический список
- •Предметный указатель
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
Г л а в а 5
ОДНОКРАТНОЕ ИЗМЕРЕНИЕ
5.1. ОДНОКРАТНОЕ ИЗМЕРЕНИЕ ПО ШКАЛЕ ПОРЯДКА. ТЕОРИЯ ИНДИКАТОРА
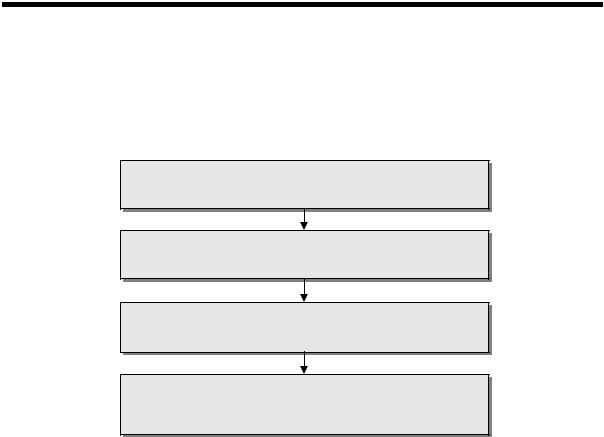
Однократное измерение по шкале порядка выполняется в последовательности,
приведенной на рис. 43.
Анализ априорной информации; определение вероятности правильного решения
Выполнение измерительной процедуры (сравнения размеров опытным путем)
Принятие решения
Представление результата измерения в форме решения с указанием его вероятности
Рис. 43.
Последовательность выполнения однократного измерения по шкале порядка
На основании анализа априорной информации устанавливается вероятность правильного решения Р. После этого выполняется основная измерительная процедура: сравнение между собой размеров Q = Qi и Qj . В зависимости от результата сравнения принимается решение относительно неравенства Q >< Qj . Результат измерения пред-
ставляет собой решение с указанием его вероятности (см. п. 4.3.1).
Иногда показателем качества результата измерения служит вероятность того, что оно является ошибочным. Если, например, известно, что при многократном выполнении таких же измерений ранее при Q < Qj в 20 % случаев принималось ошибочное решение Q ≥ Qj , то вероятность такой ошибки РI ≈ 0,2. Если в 10 % случаев при Q ≥ Qj принималось решение Q < Qj , то вероятность этой ошибки РII ≈ 0,1. Понятно, что чем больше вероятность ошибки при принятии решения, тем ниже качество результата измерения. При Q » Qj или Q « Qj вероятностями ошибок можно пренебречь. При Q ≥ Qj , Q ≤ Qj и Q ≈ Qj c ними нужно считаться. Таким образом, вероятности ошибок
100

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
зависят не только от априорной, но и от апостериорной информации – силы неравенств в выражении (6).
Разновидностью однократного измерения по шкале порядка служит контрольно-
измерительная операция, при которой случайный размер Q (например, размер какого-
нибудь серийно выпускаемого изделия при выборочном контроле) сравнивается с нормой. На основании решения опытным путем неравенства Q >< Qп , где Qп - некоторое пороговое значение случайного размера Q, связанное с нормой, изделие признается годным или бракуется. При этом возможны ошибочные решения с вероятностями ошибок как первого (Р1), так и второго (Р11) рода. Ошибкой I-го рода является признание годного изделия бракованным, а ошибкой II-го рода – пропуск брака, т.е. признание бракованного изделия годным.
Другой разновидностью однократного измерения по шкале порядка является обнаружение полезного сигнала на фоне случайных помех. Как уже отмечалось в п. 4.3.1, средства измерений, решающие задачу обнаружения, называются индикаторами. В этом случае Qп называется порогом обнаружения. На основании решения опытным путем неравенства Q >< Qп принимается одно из следующих решений:
если Q ≤ Qп , то Q представляет собой случайную помеху;
если Q > Qп , то в Q содержится полезный сигнал.
Особую сложность представляет обнаружение сигналов, мощность которых соизмерима, или даже меньше мощности помех. В этих условиях вероятность ошибочных решений очень велика. Поэтому в состав индикатора включают оптимальный (согласованный со спектром сигнала) селективный фильтр, выделяющий полезный сигнал на фоне помех. Структурная схема такого индикатора показана на рисунке 44.
Рис. 44.
Типовая структурная схема индикатора
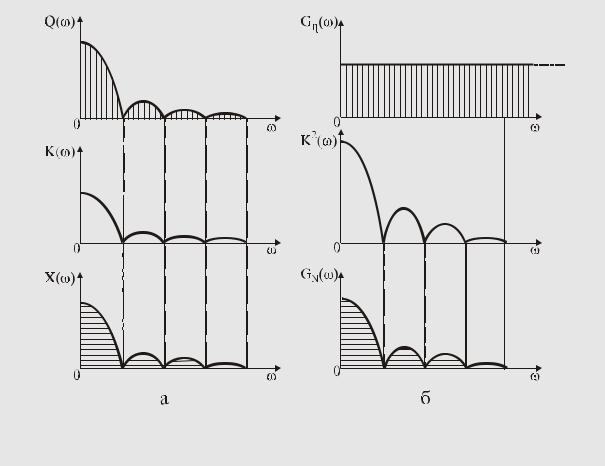
Предположим, что индикатор предназначен для обнаружения прямоугольного импульса на фоне белого шума – случайных помех со средним значением, равным нулю и равномерным энергетическим спектром G(ω) = const. Амплитудный спектр прямоугольного импульса и энергетический спектр помехи, представляющей собой напряжение тепловых шумов на выходе оптимального фильтра, показаны на рисунке 45
101
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
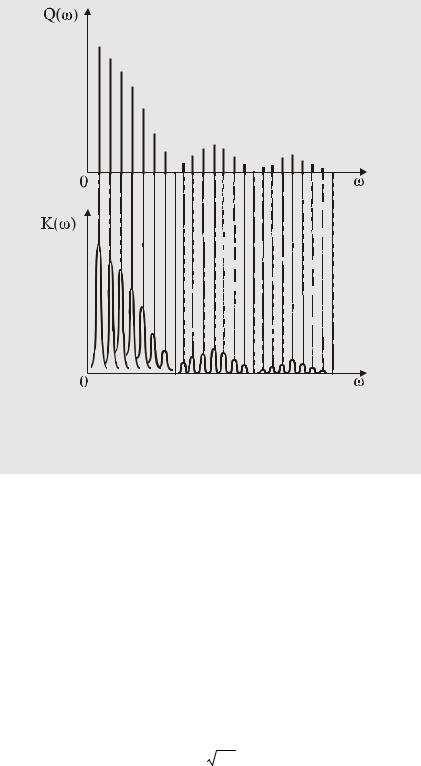
(а и б, соответственно). Если амплитудно-частотная характеристика (АЧХ) фильтра К(ω) согласована со спектром входного сигнала и имеет вид, показанный на рисунке 45а, то подавление основных энергонесущих составляющих полезного сигнала происходит незначительно, в то время, как энергия помехи ослабляется существенно. В результате отношение сигнал / помеха, пропорциональное отношению заштрихованных площадей на рис. 45, заметно отличается на входе и выходе оптимального фильтра. Выигрыш получается тем более значительным, чем сложнее входной сигнал. В этом нетрудно убедиться, рассмотрев АЧХ фильтра, оптимального последовательности прямоугольных импульсов. Как показано на рис. 46, оптимальный фильтр, получивший название гребенчатого, отфильтровывает индивидуально каждую гармонику полезного сигнала. Энергия помехи в промежутках между резонансными частотами подавляется.
Рис.45.
Прохождение полезного сигнала (а) и белого шума (б) через фильтр, оптимальный для прямоугольного импульса
Кроме того, фазочастотная характеристика (ФЧХ) оптимального фильтра такова, что в определенный момент времени t0 все гармоники полезного сигнала на выходе складываются в фазе. Достигается это благодаря тому, что фаза каждой гармоники задерживается на угол ψ(ω), равный в момент времени t0 фазе этой гармоники на входе. Тогда фаза каждой гармоники на выходе фильтра в момент времени t0
Θ(ω) = ωt0 + φ(ω) + ψ(ω) = ωt0 + φ(ω) – ωt0 – φ(ω) = 0,
гармоники складываются в фазе, образуя выброс, и максимизируется отношение пико
102
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
вой мощности сигнала к эффективной мощности помехи, ибо начальные фазы составляющих помехи случайны, и на выходе фильтра их фазы не совпадают.
Рис.46.
АЧХ гребенчатого фильтра, оптимального последовательности прямоугольных импульсов
Оптимальный фильтр искажает, конечно, форму входного сигнала, но для решения задачи обнаружения это не имеет значения.
После максимизации отношения сигнал / помеха можно с большей уверенностью приступать к решению вопроса о том, является ли мгновенное значение напряжения на выходе индикатора помехой, или совокупностью помехи и полезного сигнала. Рассмотрим решение этого вопроса на примере обнаружения сигнала на фоне нормальных случайных помех при непрерывном отсчете. Это означает наличие следующей априорной информации: мгновенное значение напряжения u на выходе индикатора при отсутствии полезного сигнала подчиняется нормальному закону распределения вероят-
ности со средним значением, равным нулю, |
и дисперсией (мощностью помех) σu2 : |
||||||
|
|
|
|
− |
u2 |
|
|
pп(u)= |
|
1 |
|
2σ2 |
|
||
|
|
|
|
||||
|
|
e |
|
u . |
(23) |
||
σu |
2 π |
|
|||||
|
|
|
|
|
|
||
103
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
При наличии полезного сигнала uc плотность вероятности совокупности сигнала и помехи на выходе индикатора
|
|
|
|
|
− |
(u − |
u |
)2 |
|
|
|
|
1 |
|
|
2σ2 |
|
||||
|
|
|
|
|
|
|||||
pсп |
(u)= |
|
|
e |
|
u . |
(24) |
|||
σu |
|
|||||||||
|
|
2 π |
|
|
|
|
|
|
||
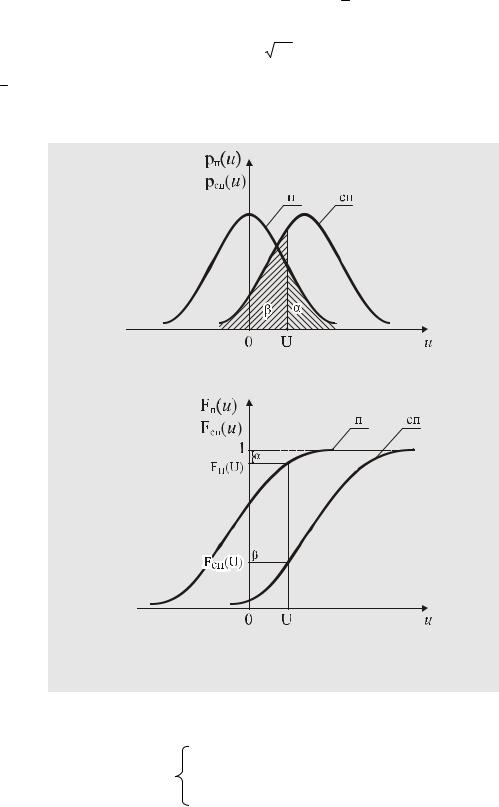
где u = uc . Графики этих зависимостей, а также соответствующие функции распределения вероятности Fп(u) и Fсп(u) приведены на рис. 47.
Рис. 47.
Вероятностно-статистические закономерности при обнаружении сигнала на фоне нормальных случайных помех
Решение о наличии полезного сигнала принимается по правилу:
при и ≤ U сигнала нет;
при и > U сигнал есть,
104
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
где U - некоторое пороговое значение напряжения. При этом опять-таки возможны ошибки двоякого рода. Ошибка I рода состоит в том, что при и ≤ U принимается решение «сигнал есть», в то время как его нет. В радиолокации, где впервые стала применяться теория статистических решений, такая ошибка называется «ложной тревогой». Вероятность этой ошибки при условии, что сигнала нет, т.е. условная вероятность ошибки I рода
α = ∞∫pп (u)d u =1− Fп (U) . |
(25) |
U |
|
Ошибка II рода состоит в том, что при и > U принимается решение «сигнала нет», в то время как он есть. В теории обнаружения такая ошибка называется «пропуском сигнала», а в радиолокации - «пропуском цели». Вероятность этой ошибки при условии, что сигнал есть, т.е. условная вероятность ошибки II рода
β = U∫pсп (u)du = Fсп (U). |
(26) |
−∞ |
|
Понятно, что вероятности ошибок желательно минимизировать. Однако, как вид-
но на рис. 47, увеличение порогового значения напряжения U, приводящее к уменьшению α, увеличивает β, и наоборот. Следовательно, выбор значения U должен быть оптимальным, удовлетворяющим противоречивым требованиям.
При дефиците априорной информации, когда о сигнале, который нужно обнаружить, ничего не известно, требования к β не могут быть сформулированы. В таком случае можно обеспечить лишь заданные требования к α. Для этого порог обнаружения U рассчитывается по формуле
α =1−Fп(U)= |
1 |
|
U |
|
|
|
|
||||
|
|
||||
2 |
−L |
σu |
, |
||
|
|
|
где L - интеграл вероятности (функция Лапласа). С помощью таблицы (например, табл. 9) находится аргумент функции Лапласа и при известной из априорной информации мощности помех устанавливается значение U.
Пример 51. При испытании объекта на электромагнитную совместимость контролируется его излучение на фиксированной частоте. Если объект удовлетворяет предъявляемым требованиям, то мгновенное значение напряжения на выходе индикатора (напряжение «шума») подчиняется нормальному закону с плотностью вероятности (23) и σu2 = 2,25 B2 . Если объект не удовлетворяет предъявляемым тре-
бованиям, то мгновенное значение напряжения на выходе индикатора подчиняется нормальному закону с плотностью вероятности (24). Рассчитать пороговое значение напряжения на выходе индикатора, обеспечивающее условную вероятность ошибки I рода α = 0,1.
Решение. |
1. Используя последнюю формулу, получим: α =1−F (U)= |
1 |
|
U |
|
= 0,1 . |
|||||
−L |
|
||||||||||
|
|
||||||||||
|
|
|
|
|
п |
2 |
|
σu |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
U |
|
|
|
. |
|
|
|
|
|
|
Отсюда |
|
= 0,4 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
L |
|
|
|
|
|
|
|
|
|||
|
σu |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
105 |
|
|
|
|
|
|
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
2.По таблице 9 находим: U =1,3
σu
3.Окончательно: U = 1,95 В.
4.Правило принятия решения формулируется следующим образом:
при u ≤ 1,95 В объект удовлетворяет предъявляемым требованиям;
при u > 1,95 В объект не удовлетворяет предъявляемым требованиям.
При этом условная вероятность ошибки I рода составляет 0,1.
Весьма поучительным является другой пример использования теории статистических решений при однократном измерении.
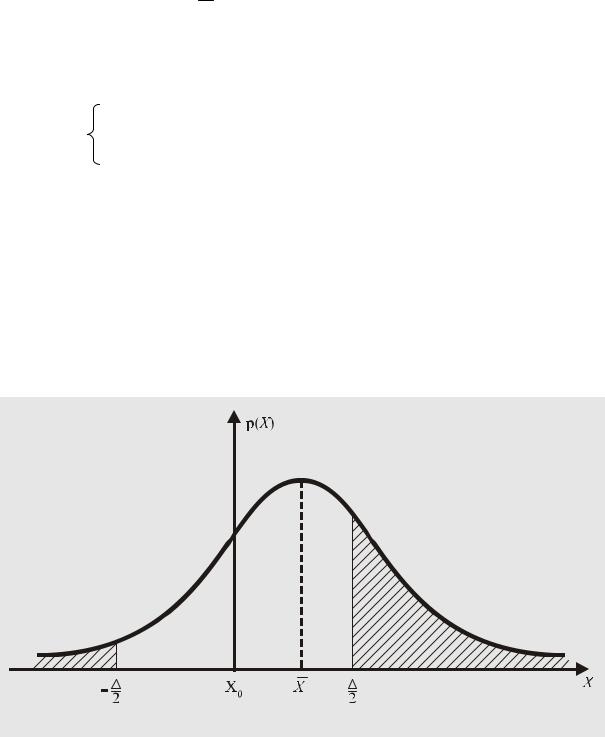
Пример 52. Определить цену деления ∆ шкалы отсчетного устройства измерительного прибора, если его показание X подчиняется нормальному закону распределения вероятности со средним квадратическим отклонением σX.
Рис. 48. К определению цены деления шкалы
106

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
Решение. Пусть решение принимается с округлением до ближайшей отметки шкалы. В нор-
мальных условиях измерений, когда поправки не вносятся, |
|
|
|
|
= |
|
|
|
≡ Q . Если |
|
|
|
|
|
удалено от отметки |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
X |
Q |
X |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
шкалы X0 не более чем на |
|
|
2 , как это показано на рис. 48, то при попадании случайного значения X |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в интервал X0 − |
2 |
; X0 |
+ |
2 |
|
|
округление его до значения X0 будет правильным решением, в то время как |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
округление до предыдущей или следующей отметки шкалы при |
|
|
X ≤ X0 − |
2 |
|
|
или |
|
|
|
X ≥ X0 + |
|
, соответст- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
венно, будет ошибкой I рода. Условная вероятность ошибки I рода, соответствующая заштрихованной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
площади на рис. 48, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X − |
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X − |
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
d X + ∞∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
α = ∫2 |
|
|
|
|
1 |
|
|
e− |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
e− |
|
|
|
|
|
|
d X = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2σ2X |
|
|
|
|
|
|
|
|
|
|
|
|
2σ2X |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
2 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∞ σX 2 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
X |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− X |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
− L |
|
|
|
|
|
|
|
|
|
|
|
= |
1 − L |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
− L |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
− L |
|
|
σ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где |
|
может быть любым в интервале от |
|
X0 − |
|
|
до X0 |
|
|
|
|
|
. |
|
Представим эту ситуацию математической |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X |
|
2 |
+ |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
моделью в виде равномерного ”закона распределения вероятности |
|
“ на интервале [ X0 − |
|
; X0 + |
] : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p( |
|
|
|
)= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Тогда среднее значение α при всех возможных значениях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
+ X |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
X |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
α = ∫p(X ) α d X =1 − |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
L |
|
σ |
X |
|
|
|
|
|
|
d X − |
|
|
|
|
|
|
L σ |
X |
|
|
|
d X . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Произведя замену переменных: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= s; d X = σX d s; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σX |
|
|
|
|
|
|
|
|
|
|
|
|
σX |
|
|
|
|
= t; d X = −σX dt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
|
σX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
|
σX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
α =1 − |
|
∫ L(s)d s + |
|
∫L(t)dt =1 − 2 |
∫L(r)d r , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σX |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где табличный интеграл:
107

И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
−r2
∫L(r)d r = r L(r)+ e 22π .
Окончательно:
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
− |
|
σX |
|
|||
|
σX |
|
e |
2 |
|
|
|
||
α =1 − 2 |
r L(r)+ |
|
|
|
|
=1 − |
|||
|
|
|
|
|
|||||
|
|
|
|
2π |
|
||||
|
|
|
|
|
|
|
0 |
|
|
Так например,
при ∆ = 4σX
при ∆ = 6σX
при ∆ = 8σX
Общая формула для цены деления шкалы имеет вид:
|
|
|
|
σX 2 |
|
− |
|
|
|
||
|
|
2 |
|
||||||||
|
|
|
+ |
|
1 − e |
2σX |
|
||||
2L |
|
|
|
|
|
|
|
|
. |
||
|
|
|
π |
|
|||||||
|
σX |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
α≈ 0,2 ;
α≈ 0,13 ;
α≈ 0,1.
≈0,8 σαX .
Втеории индикатора, если величина сигнала uc заранее известна, требования к качеству решения предъявляются в форме задания и α, и β. Порог обнаружения U и
отношение мощности сигнала к мощности помех |
u |
2 |
, обеспечивающие выполнение |
|
σ 2 |
||||
|
|
|||
|
|
u |
|
|
этих требований, находятся путем решения системы уравнений:
Fп(U)=1−α;Fсп(U)= β.
Функции распределения вероятности здесь выражаются через интеграл вероятности следующим образом:
|
|
U |
|
|
|
1 |
|
|
|
|
|
|
|
= |
−α; |
|
|||||
L |
σu |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
u |
|
|
U |
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
− |
|
|
|
= |
|
−β. |
|
L |
σu |
|
|
|
2 |
|||||
|
|
|
|
σu |
|
|
||||
Найденное в результате решения первого уравнения значение аргумента функции Лапласа подставляется во второе уравнение, после чего вновь используется табл. 9.
108

Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
Еще одним примером использования в метрологии теории статистических решений при однократном измерении по шкале порядка является обеспечение должного качества поверки или калибровки.
Технические характеристики средств измерений, оказывающие влияние на результат измерения и его качество, называются метрологическими характеристиками. На те из них, которые оказывают
существенное влияние, устанавливаются нормы. Обычно это бывает номинальное значение и допусти-
мое отклонение от него. Метрологические характеристики, на которые установлены нормы, называются
нормированными метрологическими характеристиками. Их соответствие установленным нормам должно контролироваться. Контроль нормированных метрологических характеристик средств измерений называется поверкой или калибровкой, в зависимости от того, для получения какой информации используются эти средства измерений и каковы полномочия контролирующего органа.
При поверке (калибровке) средств измерений могут совершаться ошибки как I-го, так и II-го рода. Ошибкой I-го рода является признание метрологически исправного средства измерений неисправным, а ошибкой II-го рода – метрологически неисправного исправным. И те, и другие ошибки рассматриваются как брак поверки (калибровки).
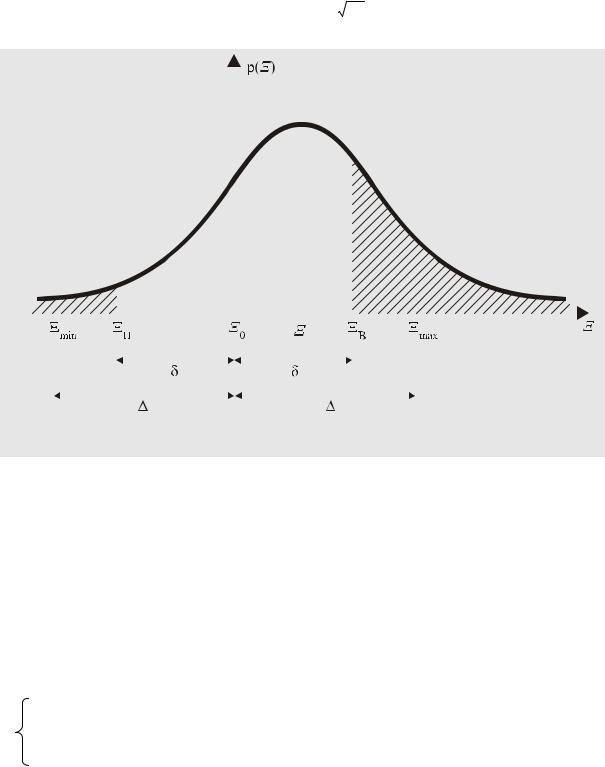
Если для метрологически исправного средства измерений
∆ = Ξmax– Ξ0 = Ξ0 – Ξmin –
допустимое отклонение нормированной метрологической характеристики Ξ от ее номинального значения Ξ0 , а
δ = Ξв – Ξ0 = Ξ0 – Ξн –
допустимое отклонение от номинала результата измерения этой метрологической характеристики с помощью рабочего эталона (будем считать, что результат измерения подчиняется нормальному закону распределения вероятности), то, как видно на рис. 49, условная вероятность ошибки I-го рода
α =1− L Ξσ−ΞΞн − L Ξвσ−ΞΞ
зависит от Ξ . У метрологически исправного средства измерений Ξ может быть любым в пределах от Ξmin до Ξmax . Поэтому среднее значение α при всех возможных значениях Ξ
|
|
1 |
|
Ξmax |
|
|
|
−Ξ |
|
|
|
Ξ |
|
− |
|
|
|
||
|
|
|
Ξ |
н |
|
Ξ |
|||||||||||||
|
|
|
|
∫ 1 |
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
α = Ξ −Ξ |
|
− L σ |
|
|
|
− L |
|
σ |
|
|
|
d Ξ . |
|||||||
|
max |
|
|
|
|
|
|
|
Ξ |
|
|
|
|
|
|
Ξ |
|
|
|
|
|
min Ξmin |
|
|
|
|
|
|
|
|
|
|
|||||||
После замены переменных:
|
Ξ |
−Ξн |
= s ; |
Ξв − |
Ξ |
|
= t , |
|
|
|
|
|
|
||
|
|
σΞ |
σΞ |
||||
ииспользования принятых обозначений, последнее выражение приводится к виду:
δ+
α =1− σΞ σ∫ΞL(r)d r ,
δ −
σΞ
109
И.Ф. Шишкин. ТЕОРЕТИЧЕСКАЯ МЕТРОЛОГИЯ
________________________________________________________________
где табличный интеграл имеет представление, приведенное в примере 52. Окончательно:
|
|
|
|
|
|
|
+ δ |
|
|
|
|
|
|
− δ |
|
|
|
|
|
|
|
|
− |
( −δ)2 |
|
− |
( +δ)2 |
|
||||||||
|
|
|
|
|
+ δ |
|
|
|
|
− δ |
|
|
1 σΞ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2σ2Ξ |
|
2σ2Ξ |
|
||||||||||||||||||||||
|
|
α =1− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
e |
|
|
|
|
− e |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
L |
|
|
|
|
|
L |
|
|
|
|
|
|
2 π |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
σΞ |
|
|
|
|
|
|
σΞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 49. К определению условной вероятности ошибки I-го рода при поверке (калибровке) средства измерений
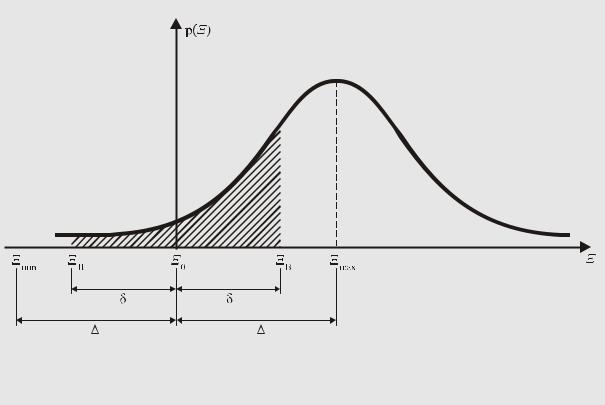
В свою очередь максимальное значение условной вероятности ошибки II-го рода, как это следует из рис. 50,
|
+ δ |
|
|
− δ |
|
|
|
|
|
||
βmax = L |
σΞ |
|
− L |
σΞ |
. |
|
|
|
|
Допустимое отклонение нормированной метрологической характеристики от ее номинального значения указывается в технической документации на средство измерений, а среднее квадратическое отклонение результата ее измерения с помощью рабочего эталона σΞ должно быть известно. Поэтому при использовании правила принятия решения:
если Ξ оказывается в пределах интервала [Ξн; Ξв], то средство измерений признается метрологически исправным; если Ξ оказывается за пределами интервала [Ξн; Ξв], то средство измерений признается метрологически неисправным,
брак поверки (калибровки) определяется выбором δ.
110
Часть I. ОБЩАЯ ТЕОРИЯ ИЗМЕРЕНИЙ
________________________________________________________________
Рис. 50.
К определению условной вероятности ошибки II-го рода при поверке (калибровке) средства измерений
Безусловная вероятность ошибки I рода по правилу умножения вероятностей равна условной вероятности, умноженной на вероятность выполнения условия Рп:
РІ = αPп .
Безусловная вероятность ошибки II рода
РII = βPcп .
Вероятности Рп и Рсп оцениваются непосредственно перед началом измерения, исходя из анализа априорной информации. Результатом измерения является одно из следующих решений:
-сигнала нет;
-сигнал есть.
Вероятность того, что первое решение является правильным, составляет 1-РII. Вероятность того, что правильным является второе решение, равна 1-PI.
111
