2.6 Равновесие в однокомпонентной двухфазной системе.

Уравнение Клаузиуса-Клапейрона

Рассмотрим двухфазную однокомпонентную систему. При равновесии в соответствии с теоремой равновесия Гиббса:

.

Так как состав фаз постоянен, то химический потенциал компонента зависит только от внешних параметров р и Т:

.

Продифференцировав, получим

.

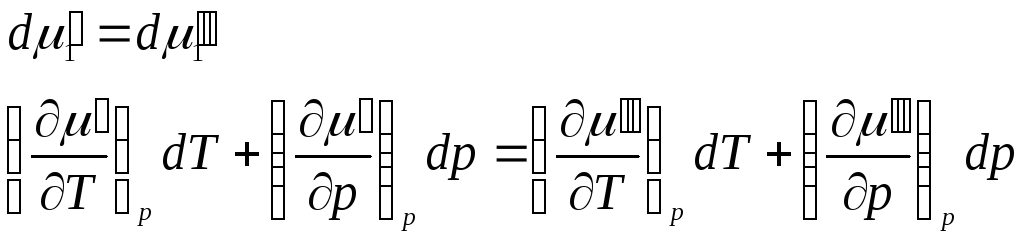Так как химический потенциал чистого компонента – есть парциальная мольная энергия Гиббса (), то

,

где - мольная энтропия компонента в первой и второй фазах соответственно;

- мольный объем компонента в первой и второй фазах соответственно.

Преобразуем:

.

Разность - есть изменение мольной энтропии при переходе вещества из фазы «′» в фазу «″», то есть это энтропия фазового превращения. Тогда

Изменение энтропии при фазовом превращении

,

где – мольная теплота фазового перехода;

Т_ф.п. – температура фазового перехода,

следовательно,

. (2.6)

Полученное уравнение (2.6) – уравнение состояния однокомпонентной двухфазной системы Клаузиуса-Клапейрона.

Применим полученное уравнение к различным процессам.

В процессе плавления производная dp/dT показывает, на какую величину нужно изменить давление, чтобы изменить температуру плавления вещества на 1 градус. Для большинства веществ плотность ρ_т > ρ_ж, тогда и. Следовательно, с повышением давления температура плавления будет увеличиваться. Еслиρ_т < ρ_ж, например, для воды (глицерина или висмута), то ии с повышением давления температура плавления будет снижаться.

Для процесса возгонки твердого вещества или испарения жидкости можно допустить, что . Если паровую фазу можно считать идеальной, то в соответствии с уравнением Менделеева-Клапейрона

,

тогда уравнение (2.6) запишется:

.

Разделив переменные и проинтегрировав в определенных пределах в узком интервале температур, считая постоянной величиной, получим

, (2.7)

где – среднее значение мольной теплоты фазового перехода в интервале температур отТ₁ до Т₂.

На основе полученного уравнения (2.7) можно рассчитать:

1. температуру кипения вещества Т₂ под давлением р₂, если известна температура кипения Т₁ этого вещества под давлением р₁ и величина средней мольной теплоты испарения;

2. давление насыщенного пара индивидуального вещества р₂ при температуре Т₂, если известно давление насыщенного пара р₁ при температуре Т₁ и средняя мольная теплота испарения;

3. среднюю мольную теплоту испарения или возгонки вещества, если известны значения давления насыщенного пара вещества при двух температурах.

2.7 Применение правила фаз Гиббса к анализу диаграммы

состояния однокомпонентной системы

Применим правило фаз Гиббса к анализу диаграммы состояния однокомпонентной системы, например, воды (рис. 2.1). В области средних давлений и средних температур вода может находиться в жидком состоянии, твердом (лед) и газообразном (пар). Так как система однокомпонентная, ее состояние характеризуется только двумя внешними параметрами:р и Т.

Рис.2.1 Диаграмма состояния воды:

ОВС – состояние жидкой воды;

АОС – состояние пара;

АОD – состояние льда;

О – тройная точка;

ОВ – кривая плавления;

ОС – кривая испарения;

ОА – кривая возгонки;

ОD – кривая давления насыщенного пара над переохлажденной водой.

Рассмотрим различные равновесные состояния системы.

1. Если вода находится в однофазном состоянии, то m = 1, тогда

.

Если C = 2, то мы можем произвольно в определенных пределах изменять два параметра: р и Т независимо друг от друга, при этом число и вид фаз системы не изменится. На диаграмме такому состоянию системы отвечают три плоскости, характеризующие состояние жидкой воды, пара и льда: OBC, AOC и AOD.

2. Если в равновесии находятся двухфазная гетерогенная система (жидкая вода – пар; жидкая вода – лед; лед – пар), то

Если С = 1, то возможно изменение только одного параметра: Т или р. На диаграмме такое состояние характеризуется тремя кривыми: ОС, ОВ и ОА, которые описываются уравнением Клаузиуса-Клапейрона. Например, если изменится температура, то в соответствии с уравнением будет меняться и давление, т.е. независимо изменяется только один параметр. Кривая ОВ показывает, что с повышением давления температура плавления льда уменьшается. Это также следует из уравнения Клаузиуса-Клапейрона.

3. Если в равновесии находится трехфазная система (вода – лед – пар), тогда

Если С = 0, то ни один из параметров состояния изменить нельзя. Это означает, что три фазы могут находиться в равновесии только при определенных условиях. На диаграмме такое состояние выражается точкой О, которая называется тройной. Если изменится Т или р, то изменится число фаз (система станет однофазной или двухфазной) и установится другое равновесное состояние.