Тема 3. Методы прогнозирования необратимых процессов

3.1. Краткосрочное прогнозирование. Модель Брауна

Ранее мы уже обсуждали идею задания разных весов в модели среднего каким-нибудь образом для получения лучшего прогноза. Эта идея становится очень актуальной в случае с необратимыми процессами, ведь, если нам в таких условиях нужно получить более адекватный прогноз, то последние данные для нас имеют большее значение, нежели старые данные. То есть в общем случае в модели:

(где νt - вес соответствующего значения Yt на наблюдении t) было бы логично задать веса следующим образом:

νT νT−1 ... ν1 .

Веса можно задавать используя разные принципы, но одним и самых эффективных с точки зрения прогнозирования является принцип, основанный на экспоненциональном характере задания весов, впервые предложенные R.G. Brown'ом:

Здесь α (носящий название постоянной сглаживания) — единственный параметр, варьируя который мы можем получать разные веса (3.1.2) для разных наблюдений.

Ряд (3.1.2) представляет собой ряд членов геометрической прогрессии. Его сумма сходится к единице:

Таким образом в модели Брауна постоянная сглаживания должна лежать в пределах (3.1.4).

С помощью экспоненциально взвешенного ряда весов легко рассчитать взвешенное среднее показателя Y в момент времени T, которое будет являться прогнозной моделью процесса на следующий момент времени T+1. Подставив в формулу (3.1.1) ряд весов из (3.1.2) получим:

37

Как видим, в (3.1.6) часть, вынесенная за скобки, представляет собой расчётное значение, вычисленный на предыдущем шаге. Тогда окончательно формулу (3.1.6) можно привести к следующему виду:

В формуле (3.1.7) появляется соблазн дать постоянной сглаживания следующую экономическую интерпретацию: α представляет собой некоторую среднюю взвешенную, служащую для формирования прогнозного значения. То есть прогноз складывается из двух частей: из части фактического значения, полученного на наблюдении t и части,

спрогнозированной на наблюдение t. В такой трактовке, очевидно, что α (0;1) , так как

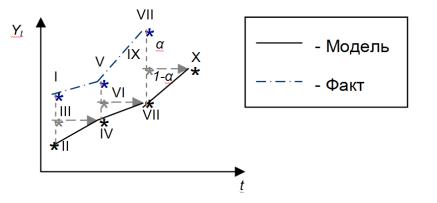
подразумевается наличие средней между двумя значениями, и именно этой трактовки модели придерживаются многие экономисты. Графически формирование прогнозного значения в соответствии с моделью (3.1.7) представлено на рисунке 11: точка III считается как средневзвешенная фактического значения I и прогнозного II, её значение как раз и становится прогнозом – точкой IV. Далее берётся средневзвешенная между точками IV и V, получается новая средняя (точка VI) и новый прогноз (точка VII) и так далее. Причём α в данной интерпретации регулирует распределение весов между фактом и прогнозом.

Рисунок 11: Графическое представление механизма формирования прогноза в модели (3.1.7)

Однако мы в данном случае сталкиваемся с ситуацией, в которой трактовка модели её только ограничивает. Покажем, каким образом это происходит.

Если мы раскроем скобки в правой части (3.1.7):

после чего вынесем за скобки α, то получим формулу, математически абсолютно идентичную формуле (3.1.7), но имеющую уже другую трактовку:

Здесь прогнозное значение формируется на основе предыдущего спрогнозированного, а α выступает некоторым коэффициентом адаптации модели к новой поступающей информации (так как в скобках в (3.1.9) у нас представлено отклонение факта от

38

прогноза). В таком случае степень адаптации может быть, в общем-то, любой: модель может адаптироваться незначительно и отсеивать поступающие «шумы» (когда альфа мал, например, составляет 0,3) или достаточно быстро адаптироваться к поступающей информации в случае, когда в процессе происходят качественные изменения (когда альфа больше 1, например, составляет 1,7). Графическое представления этой трактовки дано на рисунке 12.

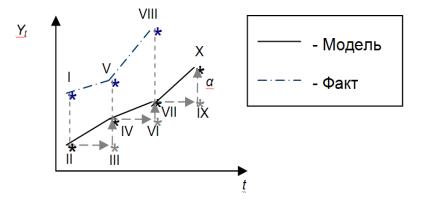
Рисунок 12: Графическое представление механизма адаптации в модели (3.1.9)

В этом случае расчётное значение II берётся за базу для прогноза на следующем наблюдении и переносится в точку III, которая затем корректируется на величину отклонения фактического значения I от расчётного II. В итоге прогнозное значение из точки III «переходит» в точку IV, которая в свою очередь становится базой для следующего прогноза (точка VI) и так далее. Постоянная сглаживания α в этой интерпретации выступает константой, регулирующей скорость адаптации, то есть то, на какую величину произойдёт корректировка модели (например, из точки III в точку IV).

Для того чтобы закончить рассмотрение различных вариантов интерпретации одной и той же модели Брауна, введём коэффициент η, такой, что:

Если α (0;2) , то, естественно, что η (− 1;1) . С учётом условия (3.1.10) мы можем

Эта модель тождественна моделям (3.1.7) и (3.1.9), однако благодаря такому представлению, трактовать её можно несколько иначе. В ней прогнозное значение на шаге t+1 полностью учитывает фактическое значение на наблюдении t, и корректируется на величину отклонения пропорционально η. Графически этот механизм может быть представлен так, как это показано на рисунке 13. По своей логике этот механизм напоминает описанный для рисунка 12, однако у него есть некоторые отличия. Так модель

39

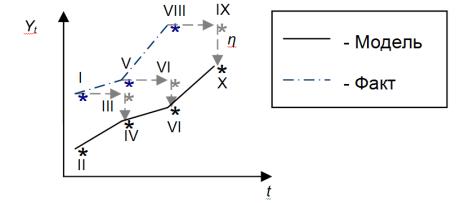
изначально формируется исходя из данного фактического значения (значение точки I переносится на следующее наблюдение в точку III), которое затем корректируется на величину отклонения факта (точка I) от прогноза (точка II) на предыдущем наблюдении. η в этой интерпретации выступает константой, не только регулирующей величину корректировки, но ещё и определяющей направление корректировки. То есть она характеризует то, на какую величину, и в какую сторону произойдёт корректировка модели (например, из точки VI вниз, в точку VII).

Рисунок 13: Графическое представление механизма адаптации в модели (3.1.12)

Как видим, вне зависимости от того, каким образом мы группируем переменные в модели, прогноз не меняется, модель Брауна даёт одни и те же результаты в любых формах её записи, однако меняется экономическая интерпретация её коэффициентов, в результате чего некоторые исследователи накладывают те или иные ограничения на модель. Это явление достаточно часто встречается в экономико-математическом моделировании: желание дать трактовку той или иной модели, тому или иному показателю, ограничивает саму модель, в результате чего она начинает работать хуже.

Рассмотрим в качестве некоторого промежуточного итога, что же характеризует коэффициент α в модели (3.1.7):

•если α = 0, то модель не учитывает текущие наблюдения (то есть становится не адаптивной),

•если α = 1, то модель не учитывает прошлые наблюдения (то есть становится полностью адаптивной),

•если α = 2, то модель не только учитывает текущие значения, но ещё и учитывает отклонения прогнозных значений от фактических на текущем наблюдении (то есть ещё и становится самообучающейся).

Если в случае с моделями обратимых процессов было понятно, каким образом находятся коэффициенты моделей, то в случае с моделью Брауна имеются некоторые вопросы. Дело в том, что модель является рекуррентной (то есть зависит от предыдущих значений), поэтому применить МНК для нахождения α использовать его невозможно. Таким образом встаёт вопрос, каким же образом задавать постоянную сглаживания.

В современной литературе существует множество различных предложений по этому поводу. Сам Браун рекомендовал брать α в пределах от 0,1 до 0,3. Однако эта

40

рекомендация имеет смысл лишь, когда мы имеем дело с эволюционным рядом с медленно меняющимися тенденциями и то для целей «сглаживания ряда». Этот принцип обычно применяется в многочисленных программах анализа рядов данных по фондовому рынку. Если же мы рассматриваем модель Брауна с позиции адаптивной модели, позволяющей давать прогнозы, то ограничивать постоянную сглаживания таким маленьким промежутком неразумно.

Один из вариантов подбора постоянной сглаживания заключается в минимизации отклонений модели от фактических значений, используя численные методы. В экселе этот функционал фактически реализован функцией «Поиск решения». То есть, когда мы будем строить модель Брауна, для нахождения оптимального α можно пользоваться этой функцией и автоматизировать процесс нахождения оптимальной постоянной сглаживания.

Если в процессе оптимизации постоянная сглаживания получилась лежащей в классических пределах – от нуля до единицы, то средняя взвешенная может использоваться для прогнозирования достаточно эффективно. Если же оптимальное значение постоянной сглаживания оказалось находящимся в запредельном множестве, то это диагностирует ситуацию, когда средняя взвешенная в принципе не может использоваться в качестве хорошей оценки прогнозного значения моделируемого процесса. В этом случае возможно два варианта действий прогнозиста.

Первый. Процесс вышел за рамки простой динамики. У него появилась некоторая тенденция в развитии. Её математическое описание в наблюдаемый промежуток времени возможно с помощью одной из эконометрических моделей.

Второй. Процесс находится на грани между эволюционной и хаотической динамикой и его математическое описание невозможно с помощью какой-либо модели. Поэтому такой процесс лучше всего прогнозировать с помощью модели Брауна, работающей в запредельном множестве.

В случае если диагностируется первая причина, то модель, которая лучше всех описывает динамику прогнозируемого экономического процесса, берётся за основу и с её помощью применяется соответствующая модификация метода Брауна. Если динамика прогнозируемого процесса не может быть описана никакими сложными эконометрическими моделями, то альтернативы применению модели Брауна с этим запредельным значением постоянной сглаживания нет.

Теперь следует указать на некоторую особенность метода Брауна, а именно – на необходимость задания начальных значений модели. Действительно, для того, чтобы «запустить» расчёт модели Брауна, то, опираясь на первое значение исходного ряда Y1,

необходимо вычислить прогнозное значение модели на втором наблюдении:

Yˆ2 = α Y1 + (1− α )Yˆ1

Первое значение этой суммы при заданном α легко вычисляется, поскольку известно значение Y1, а вот для расчёта второго слагаемого необходимо знать расчётное значение

прогнозиста нет. Очевидно, что без знания первого расчётного значения показателя модель «запустить» не удастся. Следовательно, модель Брауна следует дополнить ещё и правилом задания этого первоначального значения.

41

Существует несколько методов задания первоначального значения:

В этом варианте непонятно, почему расчётное значение должно быть равно фактическому. Кроме того ряд весов (3.1.2) для следующих значений в таком случае не сходится к 1.

2. Первое расчётное значение рассчитывается как среднее первых трёх

В этом случае неясно, почему надо брать именно такое количество наблюдений и неясно, почему у всех наблюдений один и тот же вес — 13 .

3.Модель начинает считаться с третьего значения, которое рассчитывается как средневзвешенное значение первых двух фактических через ту же постоянную сглаживания, которая используется для построения модели:

В таком случае ряд весов сходится к 1, но нет чёткого обоснования, почему именно одному фактическому значению задаётся вес α, а другому — (1-α).

4. Модель начинает строится с третьего значения, которое считается по

В этой схеме веса сходятся к 1 и сохраняется принцип, заложенный Брауном в модель

—экспоненциального сглаживания.

На самом деле проблемы задания первого значения для больших рядов фактически не

существует. Она актуальна только в случае с небольшим количеством наблюдений (например, 5 — 7) и только для ситуаций, в которых оптимальное значение постоянной сглаживания лежит в пределах 0 ;0,3 1,7 ;2 . Во всех остальных случаях проблема не стоит так остро — первое значение достаточно быстро перестаёт играть какую бы то ни было роль в формировании прогноза.

На рисунке 14 показано, какой получается модель Брауна при прогнозировании реальных процессов. В данном случае оптимальная постоянная сглаживания оказалась равной 1,002, а ошибки аппроксимации получились следующими: A f =9,62% ,

As=7,93% , R2=0,65 , C=92,36% , B=0,157 0,097i . По всем этим показателям видно, что модель получилась не такой уж и плохой и неплохо описала исходный ряд данных, соответственно можно ожидать, что и прогноз по этой модели будет точным. На графике 14 большими квадратами показаны последние 7 наблюдений, на которые осуществлялся прогноз с помощью модели Брауна. Прогноз нельзя назвать очень хорошим, но он в любом случае лучше любого прогноза, осуществляемого стандартными эконометрическими методами.

42