Ортогональность форм собственных колебаний

Собственные формы, соответствующие различным собственным частотам, ортогональны по кинетической и потенциальной энергии.

Умножим скалярно и вычтем из первого второе

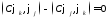, так как операторсимметричный

И, кроме того, . Тогда получим

Поскольку , то

 ортогональность по кинетической энергии

А из выражения следует ортогональность по потенциальной энергии

Пример: изгибные колебания стержня

+ граничные условия

Ортогональность по кинетической энергии

Если , то имеем обычное условие ортогональности.

Ортогональность по потенциальной энергии

13Структура спектра частот собственных колебаний. Полнота системы форм собственных колебаний

Если положительно определенный оператор, то тогда всегда существует обратный оператор, а операторвполне непрерывный. Поэтому спектр собственных частот ограниченной (по размерам) упругой системы будет дискретным с единственной точкой сгущения на бесконечности.

В окрестности бесконечно удаленной точки находится бесконечное множество частот.

В случае неограниченных систем спектр может быть сплошным

Полнота системы форм собственных колебаний

Речь идет об ограниченных упругих системах, т.е. системах с дискретным спектром собственных частот, не имеющих конечных точек сгущения.

Понятия из функционального анализа

Рассмотрим гильбертово пространство область

Пусть ортонормированная всистема функций. Числаназываются коэффициентами Фурье функции, а формальный ряд

Рядом Фурье функции по системе.

Неравенство Бесселя

Для того, чтобы ряд Фурье сходился к функции внеобходимо и достаточно, чтобы выполнялось равенство Парсевале (условие замкнутости)

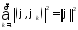
Если для ряд Фурье по системесходится к, то системаназывается полной (замкнутой) в.

Для того, чтобы система была полной внеобходимо и достаточно чтобы любую функцию из некоторого множества, плотного в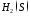, можно было сколь угодно точно приблизить линейными комбинациями функций этой системы.

Как следует из общих теорем функционального анализа, система форм собственных колебаний является полной по потенциальной и кинетической энергии.

15Энергетическое пространство упругого оператора. Энергетическая норма. Энергетическое пространство положительно определенного оператора

Пусть положительно определенный оператор в. Область определения оператораи всюду плотная в.

Введем на новое скалярное произведение

Можно убедиться, что все свойства скалярного произведения выполняются. Область с новым скалярным произведением будет пространством. Введем норму в этом пространстве, связанную с введенным скалярным произведением

Так как положительно определенный операторпоэтому

Новое нормированное пространство может оказаться не полным. Пополним его, т.е. присоединим к нему все предельные элементы последовательностей, сходящиеся по норме . Пополненное пространство будет гильбертовым пространством и оно называется энергетическим пространством оператораи обозначимс энергетической нормой.

Если , то либо, либоесть добавленный элемент, т.е. существует последовательностьтакая, чтопри. Исходное пространствои энергетическое пространство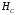изоморфны. Еслипо энергии, тои по норме исходного пространства.