36Применение асимптотического метода к расчету прямоугольных пластин

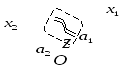
+ граничные условия при.

Порождающее решение для внутренней области

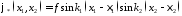
Схема решения:

1. Вблизи каждого края строим корректирующие решения – решения типа динамического краевого эффекта.

2. Корректирующее решение в сумме с порождающим решением должно удовлетворять заданным краевым условиям на заданной стороне пластины.

3. Корректирующие решения должны убывать при удалении от края во внутреннюю область.

4. Такие решения строятся у всех четырех краев. Затем производится склеивание решений. Условие склеивания дает уравнение собственных частот.

Подставим порождающее решение в уравнение колебаний

Если иизвестны, то известна и частота. Обозначимнеизвестная величина. Тогда

Строим решение типа динамического краевого эффекта для края . Для определенности рассмотрим заделанный край.

Здесь . Обозначим. Тогдаи подставим в уравнение

Характеристическое уравнение

Корни уравнения ,

соответствуют─ порождающему решению.

соответствуют корректирующему решению

Таким образом имеем

Для краевых условий имеем

Отсюда

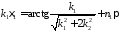
На противоположном краю

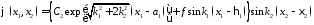
Для краевых условий при(характеристическое уравнение то же самое) имеем

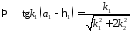
Склеиваем решения . Тогда получаем

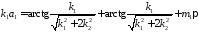
Это уравнение получается при склеивании решений в одном направлении. Аналогично, если имеем также заделки на других краях

Получаем систему уравнений для определения , т.е. для определения частот.

Для произвольных краевых условий

тангенсы фазовых постоянных

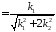(для заделки,для опирания, для стандартных опорных закреплений затабулированы)

;;

Пример

Уравнение частот

после решения которого определяются частоты

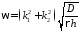
Решение уравнения частот

1.) Графически

Строятся различные линии при

Собственным частотам соответствуют точки пересечения кривых. Узлы прямоугольной сетки соответствуют частотам для пластины с граничными условиями Навье.

Для квадратной пластины , защемленной по контуру, можно получить формулу, определяющие «диагональные» частоты для случаяи

2.) Использование метода последовательных приближений

Для рассматриваемого примера

Обозначим

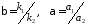
При 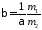берется в качестве нулевого приближения

Схема метода последовательных приближений . Пока не получим совпадение с заданной точностью.

По вычисленным определяется частота. Обычно 3 = 4 приближения дает точность 4 – 5 знаков.

37Собственные колебания круговых цилиндрических оболочек.

Рассмотрим колебания замкнутой круговой цилиндрической оболочки

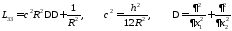
Простейший случай – краевые условия Навье

при

Эти условия эквивалентны следующим

Для краевых условий Навье можно получить точное решение

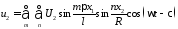
Такой вид решений принят для того, чтобы произошло разделение (сравни ). Граничные условия удовлетворяются. Если подставить эти ряды в исходные уравнения, то для каждого сочетанияиполучим систему линейных уравнений для. Обозначим для удобства. Тогда

(*)

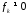Условие существования ненулевого решения

Здесь при(инерционные члены)

Раскроем определитель

Имеем 3 значения для частоты . Для каждого значения, подставляя его в систему (*) найдем

Если зафиксировать и, то получим три значения для частотыи соответствующие им формы колебаний

Имеем три функциональные степени свободы.

число полуволн формы колебаний в продольном направлении

число волн формы колебаний в окружном направлении

нет узловых точек

2 узловые точки

4 узловые точки

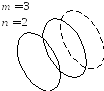
Для трех форм узловые линии будут одни и те же. Выделяют 3 различных класса форм:

1. Преимущественно поперечные формы

2. Преимущественно продольные формы

3. Преимущественно крутильные формы

Обычно низшей (основной) частоте соответствует самая простая форма колебаний (для стержней, пластин). Для оболочек это не так. Минимальному значению частоты соответствует не самая простая форма.

Для поперечных движений минимальное значение частоты достигается при . В этом случае можно пренебречь членами (как для пологих оболочек)

Общие положения, касающиеся ортогональности форм собственных колебаний, остаются справедливыми и в оболочках. Элементы есть вектор – функции (нужно брать сумму произведений соответствующих координат)

Тогда условие ортогональности по кинетической энергии запишется