
- •1Принцип Гамильтона-Остроградского для упругого тела.Вариационный вывод уравнений колебаний и естественных граничных условий для упругого тела Принцип Гамильтона – Остроградского для упругого тела
- •2Динамические уравнения теории упругости.
- •3Вариационный вывод уравнений колебаний и естественных граничных условий для одномерных и двумерных систем.
- •6Уточненная теория изгибных колебаний стержней. Уравнения балки Тимошенко
- •7Уравнения колебаний и естественные граничные условия колебаний пластин. Уравнение изгибных колебаний пластин
- •8Применение принципа Даламбера для вывода уравнений динамики упругих систем
- •Продольные колебания стержней
- •Пластина
- •10Операторное уравнение для определения спектров
- •Ортогональность форм собственных колебаний
- •13Структура спектра частот собственных колебаний. Полнота системы форм собственных колебаний
- •15Энергетическое пространство упругого оператора. Энергетическая норма. Энергетическое пространство положительно определенного оператора
- •16Вариационные принципы теории собственных колебаний. Основной вариационный принцип теории собственных колебаний
- •17Минимальное свойство низшей собственной частоты Теоремы сравнения
- •Теоремы сравнения
- •Классификация методов
- •19 Методы физической дискретизации(Дискретизация масс)
- •20Вариационные методы определения собственных частот и форм колебаний. Вариационная формулировка задачи
- •21Метод Релея и некоторые оценки, вытекающие из него: формулы Данкерли и Саутвелла Формула Релея
- •Некоторые оценки, вытекающие из формулы Релея. Формулы Данкерли и Саутвелла
- •22Вариационный метод Ритца
- •23Метод БубноваГалеркина
- •24Продольные, крутильные и изгибные колебания стержней постоянного поперечного сечения. Продольные колебания стержней постоянного поперечного сечения
- •Изгибные колебания стержней постоянного поперечного сечения
- •26Метод начальных параметров в задачах об изгибных колебаниях стержней
- •Матричная форма метода начальных параметров
- •27Методы расчленения в теории собственных колебаний стержней (метод динамических податливостей, метод динамических жесткостей).
- •28Влияние осевых усилий на собственные изгибные колебания стержней
- •29Влияние инерции вращения и деформаций поперечного сдвига на изгибные колебания стержней
- •30Собственные колебания прямоугольных пластин.Граничные условия Навье. Уравнения и граничные условия
- •Собственные колебания прямоугольной пластины с краевыми условиями Навье
- •31Плотность собственных частот пластин
- •32Прямоугольная пластина краевыми условиями Леви
- •33Колебания круговых и кольцевых пластин
- •Круговые пластины
- •34Применение вариационных методов в задачах о собственных колебаниях пластин
- •35Асимптотический метод в.В.Болотина для определения спектров собственных колебаний
- •Идея асимптотического метода
- •36Применение асимптотического метода к расчету прямоугольных пластин
- •37Собственные колебания круговых цилиндрических оболочек.
- •38Осесимметричные и преимущественно изгибные колебания. Осесимметричные колебания цилиндрических оболочек
- •39Собственные колебания пологих оболочек. Уравнения и граничные условия
- •40Волны в неограниченной упругой изотропной среде. Волны расширения и волны сдвига.
- •41Дисперсионное уравнение. Фазовая и групповая скорости.Типы дисперсий
- •42Поверхностные волны Релея
- •43Приложение к сейсмологии
- •44 Продольные волны и волны кручения в призматических стержнях.Элементарная и уточненная теории изгибных волн в стержнях.
- •Волны кручения в призматическом стержне
- •Изгибные волны в призматических стержнях
- •Изгибные волны в стержнях
7Уравнения колебаний и естественные граничные условия колебаний пластин. Уравнение изгибных колебаний пластин
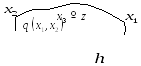
Выполняются классические гипотезы Кирхгофа – Лява теории пластин:
Усилия в срединной плоскости отсутствуют;
Существенные компоненты тензора деформаций

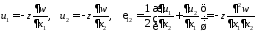
Закон Гука

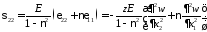
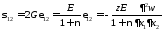
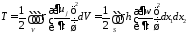

 цилиндрическая жесткость
цилиндрическая жесткость





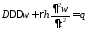
Граничные
условия на краю


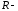 радиус кривизны в некоторой точке
контура
радиус кривизны в некоторой точке
контура
а) защемленный край

б) шарнирно опертый край

а) свободный край

8Применение принципа Даламбера для вывода уравнений динамики упругих систем
Обычный способ получения уравнений движения механических систем основан на применении принципа Даламбера. Если уравнения равновесия системы известны, то вводя в рассмотрение силы инерции и используя квазистатические соображения, легко получаются соответствующие уравнения движения.
Пример.
Если
 инерциальная система, то
инерциальная система, то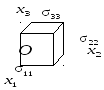
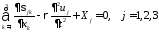
 массовые активные силы,
массовые активные силы, даламберовы силы инерции
даламберовы силы инерции
Продольные колебания стержней
Считаем, что
 ,
где
,
где внешняя
внешняя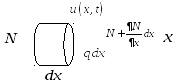
распределенная нагрузка,
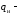 инерционная
инерционная
нагрузка.
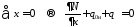
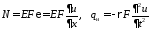

Изгибные
колебания
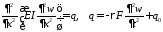

Пластина
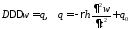
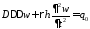
Принцип Даламбера прост, но преимущество принципа Гамильтона – Остроградского в том, что он дает возможность сведения трехмерной динамической задачи к двумерным и одномерным общим и единообразным методом; позволяет получить также динамические (естественные) граничные условия.
10Операторное уравнение для определения спектров
собственных колебаний (собственных частот и форм.)
Иллюстрацию свойств спектров собственных колебаний будем проводить на примере изгибных колебаний стержней, дифференциальное уравнение колебаний которых имеет вид

Граничные условия примем, например, следующими

Уравнению можно удовлетворить, если положить

где
 собственная
частота (круговая) подлежит определению,
собственная
частота (круговая) подлежит определению, начальная фаза,
начальная фаза, форма колебаний.
форма колебаний.
После подстановки получим

Это
есть однородная краевая задача на
собственные значения. Значения
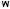 ,
при которых существует нетривиальное
решение этой задачи, называются
собственными частотами
,
при которых существует нетривиальное
решение этой задачи, называются
собственными частотами

а соответствующие им нетривиальные решения

собственные формы колебаний.
Дифференциальное выражение совместно с граничными условиями задает дифференциальный оператор, который переводит некоторое множество из одного пространства в другое.
Уравнение малых колебаний распределенных упругих систем можно записать в виде

где
 и
и линейные
дифференциальные операторы по
пространственным переменным,
линейные
дифференциальные операторы по
пространственным переменным, элемент некоторого функционального
пространства при любом фиксированном
элемент некоторого функционального
пространства при любом фиксированном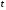 .
Как следует из принципа Гамильтона -
Остроградского,
.
Как следует из принципа Гамильтона -
Остроградского, градиент потенциальной энергии упругой
деформации, инерционный оператор,
градиент потенциальной энергии упругой
деформации, инерционный оператор, градиент кинетической энергии, упругий
оператор.
градиент кинетической энергии, упругий
оператор.
Полагая
 ,
получим задачу отыскания спектра
колебаний в операторной форме
,
получим задачу отыскания спектра
колебаний в операторной форме

где
 скалярная,
векторная или тензорная функция.
скалярная,
векторная или тензорная функция.
11Свойства
дифференциальных операторов
 и
и (упругого и инерционного операторов)
(упругого и инерционного операторов)
Будем
рассматривать эти операторы в гильбертовом
пространстве функций
 ,
где
,
где некоторая
область из евклидова пространства
некоторая
область из евклидова пространства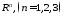 .
Например,
.
Например, при
при .
Скалярное произведение и норма
.
Скалярное произведение и норма

Пусть
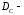 область определения оператора
область определения оператора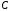 ,
,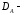 область определения оператора
область определения оператора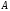 .
Оператор
.
Оператор всегда имеет более высокие производные
по координатам, чем оператор
всегда имеет более высокие производные
по координатам, чем оператор .
Поэтому
.
Поэтому
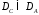 ,
,
т.е.
область определения оператора
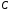 составляет подмножество
составляет подмножество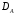 .
.
1.
Оператор
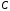 ,
как всякий дифференциальный оператор,
являетсянеограниченным.
,
как всякий дифференциальный оператор,
являетсянеограниченным.
Иллюстративный пример.
При
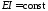 оператор
оператор .
Область определения этого оператора
.
Область определения этого оператора ,
имеющие непрерывные производные до
4-го порядка включительно и удовлетворяют
граничным условиям
,
имеющие непрерывные производные до
4-го порядка включительно и удовлетворяют
граничным условиям

Для ограниченных операторов выполняется условие

Вычислим
норму оператора
 ,
,

на множестве функций
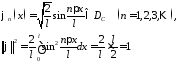
Так как
 ,
,
то
 при
при
2.
Оператор
 являетсясимметричным, т.е.
являетсясимметричным, т.е.
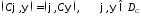
Для
примера
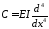 ,
, .
.


Здесь внеинтегральные члены в силу граничных условий равны нулю.
3.
Оператор
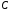 являетсясамосопряженным, т.е. он
симметричен и, кроме того, из тождества
являетсясамосопряженным, т.е. он
симметричен и, кроме того, из тождества

где
 и
и фиксированы, а
фиксированы, а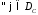 следует, что
следует, что ,
а
,
а
По
другому: если сопряженный оператор
 имеет ту же область определения
имеет ту же область определения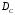 и
и на
на
4.
Операторы
 и
и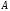 положительно
определенные.
положительно
определенные.
Симметричный
оператор
 называется положительным, если для
называется положительным, если для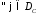 имеет место неравенство
имеет место неравенство причем
причем тогда и только тогда, когда
тогда и только тогда, когда .
.
Симметричный
оператор
 называется положительно определенным,
если для
называется положительно определенным,
если для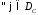 справедливо неравенство
справедливо неравенство где
где ,
или по-другому
,
или по-другому

Если оператор положительный, но не положительно определенный, то это означает, что системе можно сообщить сколь угодно большое смещение по норме, затратив на это сколь угодно малую энергию.

Положительная
определенность операторов
 и
и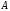 есть следствие положительной определенности
потенциальной энергии упругой деформации
есть следствие положительной определенности
потенциальной энергии упругой деформации и кинетической энергии
и кинетической энергии .
.
12Действительность частот собственных колебаний.Ортогональность собственных форм по потенциальной и кинетической энергии.
Пусть
 квадрат собственной частоты, а
квадрат собственной частоты, а соответствующая ей собственная форма
колебаний
соответствующая ей собственная форма
колебаний
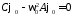
Умножим
скалярно на


Так
как
 и
и ,
то
,
то .
.
