3Вариационный вывод уравнений колебаний и естественных граничных условий для одномерных и двумерных систем.

Уравнение продольных колебаний стержней

Существенные компоненты тензора напряжений и деформацийи. Остальные равны нулю. Гипотеза плоских сечений

площадь поперечного сечения – медленно меняющаяся функция

Из имеем

Естественные граничные условия

при

Или

при

Если , то

скорость продольных волн

Если на торцах стержня заданы внешние сосредоточенные силы, то граничные условия примут вид

4 Уравнение продольных, крутильных и изгибных колебаний стержней.

Уравнение продольных колебаний стержней

Существенные компоненты тензора напряжений и деформаций и. Остальные равны нулю. Гипотеза плоских сечений

площадь поперечного сечения – медленно меняющаяся функция

Из имеем

Естественные граничные условия

при

Или

при

Если , то

скорость продольных волн

Если на торцах стержня заданы внешние сосредоточенные силы, то граничные условия примут вид

Уравнение крутильных колебаний стержней

интенсивность внешней нагрузки (распределенный крутящий момент). Депланационные эффекты не учитываются. Используется классическая теория кручения стержней. Центр масс в каждом сечении совпадает с центром жесткости.

Интеграл действия имеет вид

момент инерции массы стержня единичной длины относительно оси.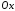

Уравнение изгибных колебаний стержней

Оси главные центральные оси инерции. Справедливы гипотезы Бернулли (гипотеза плоских сечений). Из них следует

Существенные компоненты тензоров напряжений и деформаций

Интеграл действия имеет вид

Естественные граничные условия (если концы стержня свободны от внешних сил)

при

5Поправка Релея для случая продольных колебаний стержней

При выводе уравнений продольных колебаний стержней предполагалось, что . Однако в силу эффекта Пуассона поперечные перемещения будут отличны от нуля. Уточнение уравнений с учетом этого обстоятельства проделано Релеем в 1877

Пусть стержень имеет две оси симметрии. Тогда в начале координат при перемещения. После интегрирования получим

Изменится выражение для кинетической энергии

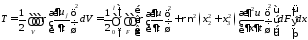
─ полярный момент ирерции

Применим принцип Гамильтона – Остроградского и получим уравнение колебаний, учитывающее эффект Пуассона

Однако поправка Релея не учитывается. Покажем это. Пусть

характерное время (например, период)

характерный размер поперечного сечения

характерный размер изменения напряженно-деформированного состояния по оси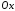

Тогда

Порядок отношения этих величин

Таким образом, учет влияния поперечных перемещений является некорректным при . Если, т.е. характерная длина формы колебаний сопоставима с характерным размером поперечного сечения, то поправка существенна. Но тогда исходное уравнение не работает.

6Уточненная теория изгибных колебаний стержней. Уравнения балки Тимошенко

Впервые уточнение классической теории, основанной на гипотезах Бернулли, было сделано Релеем. Он учел инерцию вращения

Инерционные силы от поворота сечения . Спроектируем их на нормаль и добавим в уравнение

Спустя лет (1915 г.) С.П.Тимошенко показал, что это уточнение неправомерно. Вклад дополнительного члена в энергию имеет порядоки если учитывать инерцию вращения, то необходимо учитывать и деформацию поперечных сдвигов.

для согласования правила знаков

, если

В рамках классической теории

В силу наличия сдвигов сечения не будут плоскими и перпендикулярными к деформированной оси стержня. Тимошенко предложил: сечения остаются плоскими, но не перпендикулярными к изогнутой оси балки.

некоторый осредненный угол сдвига; угол между нормалью к изогнутой оси балки и следом плоскости поперечного сечения. Этот угол считается пропорциональным поперечной силе.

Тогда

инезависимые функции

Для балки Тимошенко тоже существенная компонента тензора деформаций

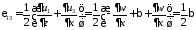
Гипотеза о ненадавливаемости волокон сохраняется.

Вычислим потенциальную энергию упругой деформации

Оценим порядок энергии сдвига. Поперечная сила .

Формула Журавского

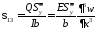
Пусть характерный прогиб;

характерное время (период);

характерный размер поперечного сечения;

характерная длина (например, длина полуволны изменения прогиба)

Тогда

Энергия деформаций изгиба

Поправка на сдвиг по энергии имеет порядок

Учет энергии сдвига необходим при

Кинетическая энергия

Оценим порядок слагаемых

Поправка на инерцию вращения имеет порядок

Т.е. также как и для соотношения энергии сдвига и энергии изгиба

Линейная плотность лагранжиана

Из условия имеем

Учитывая вид лагранжиана, получим

(1)

(2)

Естественные граничные условия

при

при()

Кинематические условия заделка

Неизвестные функции в уравнениях (1) и (2) и

Продифференцируем уравнение (2) и вычтем уравнение (1)

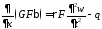(2’)

Уравнения (2) и (2’) – новая система

Пусть . Тогда из уравнения (2’) получим

Исключая из первого уравнения, получим

Получили уравнение Тимошенко. Точнее оно имеет вид

Где коэффициент, зависящий от формы поперечного сечения. Наличие коэффициента ─ следствие того, что сдвиги неравномерно распределены по поперечному сечению стержня. Для прямоугольного поперечного сечения. Вообще этот параметр можно определить по следующей формуле

Тимошенко вычислял энергию сдвига, полагая, что касательные напряжения распределены по формуле Журавского и получил формулу

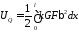, где

Такой подход несколько непоследовательный, хотя и дает хорошие результаты. Если , то получим уравнение колебаний по классической теории изгиба стержней.