31Плотность собственных частот пластин

При изучении спектров собственных колебаний возникает вопрос об оценке количества частот, приходящихся на единицу частотного диапазона. Введем асимптотическую оценку для числа частот , удовлетворяющих условию. Упорядочим спектр собственных частот, например, для пластины с краевыми условиями Навье.

Обозначим (волновые числа). Тогда

Рассмотрим плоскость волновых чисел

Частоты располагаются в узлах сетки. Подсчитаем число частот, меньших заданного значения: зафиксируем . ()

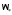Нужно подсчитать количество точек (частот), расположенных внутри четверти круга с радиусом . Найдем приближенное, асимптотическое значение. Вычислим площадьи разделим на площадь ячейки.

Эта формула при больших достаточно определяет.

Плотность частот

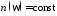для пластины с краевыми условиями Навье, т.е. частоты распределены равномерно в частотных диапазонах.

Аналогично можно определить распределение частот для пластин с другими краевыми условиями, а также для оболочек.

32Прямоугольная пластина краевыми условиями Леви

Для определенности рассмотрим заделку по противоположным кромкам. Тогда граничные условия будут следующими

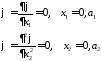
Решение ищем в виде ряда

После подстановки получим

Краевые условия для

,

где ,

Подставим в краевые условия и приравняем нулю определитель коэффициентов при 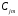. Получим уравнение частот

33Колебания круговых и кольцевых пластин

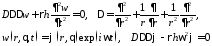
Задача состоит в нахождении общего решения. Используем метод факторизации, раскладывая оператор на множители

и рассматриваются два уравнения

Решение удовлетворяет исходному уравнению. Еслии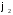содержат линейно независимые решения, тоявляется фундаментальной системой решений уравнения.

Круговые пластины

По окружной координате произойдет разделение переменных. Подставим в уравнения, которые получились после применения метода факторизации. Получим уравнения Бесселя

Решением первого уравнения являются функции Бесселя мнимого аргумента

второго - действительного

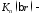функция Макдональда,функция Неймана

Общее решение

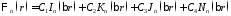
Если пластина сплошная, то , т.к. функциив нуле приимеют особенность.

Граничные условия на контуре, например, 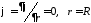или

Уравнение частот

имеет бесконечное счетное множество корней ,номер корня,номер разложения по косинусам.

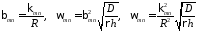
Формы собственных колебаний

Форму собственных колебаний характеризуют числа и:

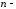количество узловых диаметров;

число узловых окружностей

по радиусу узловых линий нет

одна узловая окружность и т.д.

Сама форма ,

где некоторый коэффициент

34Применение вариационных методов в задачах о собственных колебаниях пластин

Прямоугольные пластины. Формула Релея

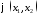,удовлетворяет, по крайней мере, кинематическим граничным условиям.

Круговые пластины. Формула Релея

Метод Ритца

см. выше в формулах Релея

Приравнивание нулю определителя коэффициентов при дает частотное уравнение. В одночастотном приближении получаем формулу Релея. Методы справедливы для пластин с переменными параметрами.

Метод Стодолы

Основан на методе Релея – Ритца. Разработан и используется для круглых пластин переменной толщины (дисков турбин)

Решение ищется в виде

некоторый параметр (), по которому в дальнейшем проводится минимизация. Приближающие функциивообще говоря не удовлетворяют даже кинематическим граничным условиям.

Применяется формула Релея и по параметру проводится минимизация функции. Используется свойство экстремальности собственных частот

Этот метод широко используется для расчета дисков переменной толщины.

Если , то интегралы легко вычисляются. Получается достаточно хорошая оценка.