
- •1Принцип Гамильтона-Остроградского для упругого тела.Вариационный вывод уравнений колебаний и естественных граничных условий для упругого тела Принцип Гамильтона – Остроградского для упругого тела
- •2Динамические уравнения теории упругости.
- •3Вариационный вывод уравнений колебаний и естественных граничных условий для одномерных и двумерных систем.
- •6Уточненная теория изгибных колебаний стержней. Уравнения балки Тимошенко
- •7Уравнения колебаний и естественные граничные условия колебаний пластин. Уравнение изгибных колебаний пластин
- •8Применение принципа Даламбера для вывода уравнений динамики упругих систем
- •Продольные колебания стержней
- •Пластина
- •10Операторное уравнение для определения спектров
- •Ортогональность форм собственных колебаний
- •13Структура спектра частот собственных колебаний. Полнота системы форм собственных колебаний
- •15Энергетическое пространство упругого оператора. Энергетическая норма. Энергетическое пространство положительно определенного оператора
- •16Вариационные принципы теории собственных колебаний. Основной вариационный принцип теории собственных колебаний
- •17Минимальное свойство низшей собственной частоты Теоремы сравнения
- •Теоремы сравнения
- •Классификация методов
- •19 Методы физической дискретизации(Дискретизация масс)
- •20Вариационные методы определения собственных частот и форм колебаний. Вариационная формулировка задачи
- •21Метод Релея и некоторые оценки, вытекающие из него: формулы Данкерли и Саутвелла Формула Релея
- •Некоторые оценки, вытекающие из формулы Релея. Формулы Данкерли и Саутвелла
- •22Вариационный метод Ритца
- •23Метод БубноваГалеркина
- •24Продольные, крутильные и изгибные колебания стержней постоянного поперечного сечения. Продольные колебания стержней постоянного поперечного сечения
- •Изгибные колебания стержней постоянного поперечного сечения
- •26Метод начальных параметров в задачах об изгибных колебаниях стержней
- •Матричная форма метода начальных параметров
- •27Методы расчленения в теории собственных колебаний стержней (метод динамических податливостей, метод динамических жесткостей).
- •28Влияние осевых усилий на собственные изгибные колебания стержней
- •29Влияние инерции вращения и деформаций поперечного сдвига на изгибные колебания стержней
- •30Собственные колебания прямоугольных пластин.Граничные условия Навье. Уравнения и граничные условия
- •Собственные колебания прямоугольной пластины с краевыми условиями Навье
- •31Плотность собственных частот пластин
- •32Прямоугольная пластина краевыми условиями Леви
- •33Колебания круговых и кольцевых пластин
- •Круговые пластины
- •34Применение вариационных методов в задачах о собственных колебаниях пластин
- •35Асимптотический метод в.В.Болотина для определения спектров собственных колебаний
- •Идея асимптотического метода
- •36Применение асимптотического метода к расчету прямоугольных пластин
- •37Собственные колебания круговых цилиндрических оболочек.
- •38Осесимметричные и преимущественно изгибные колебания. Осесимметричные колебания цилиндрических оболочек
- •39Собственные колебания пологих оболочек. Уравнения и граничные условия
- •40Волны в неограниченной упругой изотропной среде. Волны расширения и волны сдвига.
- •41Дисперсионное уравнение. Фазовая и групповая скорости.Типы дисперсий
- •42Поверхностные волны Релея
- •43Приложение к сейсмологии
- •44 Продольные волны и волны кручения в призматических стержнях.Элементарная и уточненная теории изгибных волн в стержнях.
- •Волны кручения в призматическом стержне
- •Изгибные волны в призматических стержнях
- •Изгибные волны в стержнях
1Принцип Гамильтона-Остроградского для упругого тела.Вариационный вывод уравнений колебаний и естественных граничных условий для упругого тела Принцип Гамильтона – Остроградского для упругого тела
Сначала сформулируем этот принцип для систем с конечным числом степеней свободы, подчиненных голономным идеальным связям и загруженных консервативными силами:
Среди
всех движений, совместимых со связями,
достаточно близких к истинному и
совпадающих с истинным в начальный
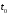 и конечный
и конечный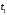 моменты времени, истинное движение
сообщает интегралу действия
моменты времени, истинное движение
сообщает интегралу действия
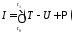
стационарное значение, т.е.
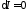
Этот принцип переносится и на распределенные системы, когда внешние силы обладают потенциалом.
 кинетическая
энергия системы;
кинетическая
энергия системы;
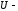 потенциальная
энергия упругой деформации;
потенциальная
энергия упругой деформации;
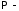 потенциальная
энергия внешних сил, равная работе
внешних сил с обратным знаком.
потенциальная
энергия внешних сил, равная работе
внешних сил с обратным знаком.
Рассмотрим
упругое тело, занимающее объем
 ,
загруженное по части поверхности
,
загруженное по части поверхности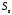 ,
а на части поверхности
,
а на части поверхности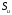 заданы перемещения точек поверхности.
заданы перемещения точек поверхности.
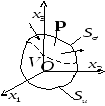
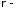 объемная плотность упругого тела
объемная плотность упругого тела
 ─ нагрузка
─ нагрузка
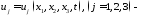 компоненты
вектора перемещений точек упругого
тела
компоненты
вектора перемещений точек упругого
тела
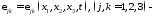 компоненты
тензорного поля деформаций упругого
тела
компоненты
тензорного поля деформаций упругого
тела
Будем считать, что перемещения и градиенты перемещений малы. Тогда компоненты тензора малых деформаций определятся формулами Коши
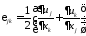
Материал
– линейно-упругий, справедлив закон
Гука
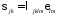
Кинетическая энергия
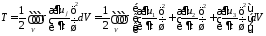
Потенциальная энергия упругой деформации
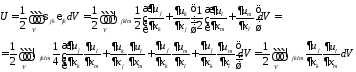 Здесь
учтено, что
Здесь
учтено, что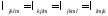 .
.
Потенциальная энергия внешних сил
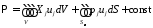
где
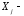 объемные силы. Без ограничения общности
объемные силы. Без ограничения общности
Запишем интеграл действия в виде
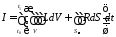 ,
,
где

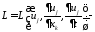 объемная плотностьлагранжиана
объемная плотностьлагранжиана
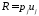
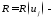 поверхностная плотностьлагранжиана
поверхностная плотностьлагранжиана
Функционал
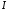 определен на функциях
определен на функциях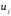 ,
имеющих необходимые производные и
удовлетворяющие заданным условиям на
поверхности
,
имеющих необходимые производные и
удовлетворяющие заданным условиям на
поверхности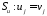 ,
т.е. кинематическим граничным
условиям.Вычислим вариацию квадратичного
функционала
,
т.е. кинематическим граничным
условиям.Вычислим вариацию квадратичного
функционала

Здесь
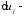 вариации
по Гамильтону: малые; совместимые со
связями, изохронные (переставимость
операций дифференцирования и варьирования);
в начале и в конце движения
вариации
по Гамильтону: малые; совместимые со
связями, изохронные (переставимость
операций дифференцирования и варьирования);
в начале и в конце движения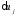 равны нулю
равны нулю
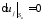 ,
, .
.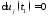 ,
,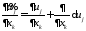
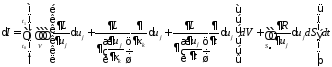
Преобразуем интегралы с использованием формулы Гаусса – Остроградского
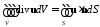 ;
в компонентах
;
в компонентах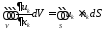
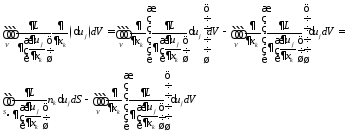
Здесь
учтено, что на
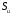
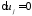 .
. Выражение
для вариации функционала
Выражение
для вариации функционала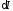 примет вид
примет вид
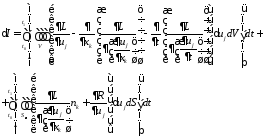
Необходимое
условие стационарности функционала
 .
Тогда на основании основной леммы
вариационного исчисления имеем уравнение
Эйлера – Остроградского.
.
Тогда на основании основной леммы
вариационного исчисления имеем уравнение
Эйлера – Остроградского.
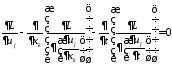 в объеме
в объеме
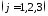
Естественные граничные условия
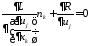 на поверхности
на поверхности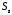
2Динамические уравнения теории упругости.
Уравнение колебаний
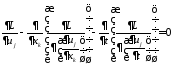 в объеме
в объеме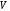
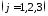
Естественные граничные условия
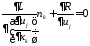 на поверхности
на поверхности

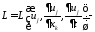 объемная плотностьлагранжиана
объемная плотностьлагранжиана
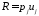
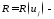 поверхностная плотностьлагранжиана
поверхностная плотностьлагранжиана
Учитывая
выражения для объемной и поверхностной
плотности лагранжиана
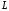 и
и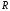 ,
получим динамические уравнения теории
упругости
,
получим динамические уравнения теории
упругости
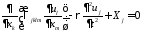 в объеме
в объеме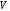
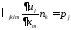 на поверхности
на поверхности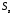
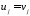 на поверхности
на поверхности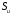
+ начальные условия
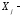 объемные силы
объемные силы
В
уравнении движения под знаком
дифференцирования
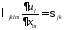
В
случае изотропного материала
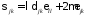
где
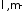 постоянные Ламе
постоянные Ламе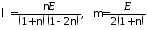 .
Тогда для изотропного материала имеем
.
Тогда для изотропного материала имеем
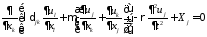
или
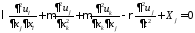
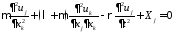 - уравнения Ламе для динамического
случая. Естественные граничные условия
- уравнения Ламе для динамического
случая. Естественные граничные условия
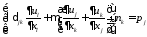 на
на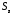
Векторная
форма записи при
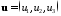 и при
и при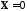
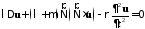
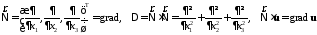
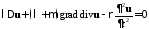
+ граничные и начальные условия.
