Решение

В данной задаче о плотности ничего не упоминается. Следовательно, она предполагается постоянной и равной единице и масса фигуры численно равна ее площади. Отсюда получаем:

Рисунок. 1.32

ПРИМЕР 3.Найти центр тяжести фигуры, ограниченной двумя параболамии.

Решение

Для нахождения координат центр тяжести достаточно вычислить по заданной области три интеграла, определяющие массу и статические моменты этой области (рис.1.33):

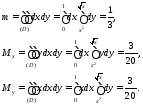
Рисунок. 1.33

Координаты центра тяжести равны:

Следовательно, .

ПРИМЕР 4.Найти момент инерции круга радиусаrотносительно точки, лежащей на окружности.

Решение

Составим уравнение окружности, проходящей через начало координат:

и вычислим момент инерции 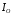. Получим:.

Вычислим интеграл в полярных координатах.

В полярной системе координат уравнение данной окружности представится в виде . Получим:

I_O= 2= 2===

= =.

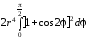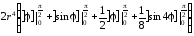ПРИМЕР 5.Вычислить момент инерции площади эллипсаотносительно оси ординат.

Решение

ПРИМЕР 6.Вычислить момент инерции площади, ограниченной параболой и прямой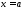относительно прямой.

Решение

Как видно из чертежа (рис. 1.34), расстояние любой точки (x,y) фигуры (D) до осибудет равно, а квадрат расстояния. Следовательно,

.

Рисунок. 1.34

2. Тройные интегралы

2.1. Задача о вычислении массы тела

Рассмотрим тело (V), плотность которого известна, но переменна, т.е. в разных точках различна, и предположим, что нам требуется подсчитать массуэтого тела. Для этого разобьем тело (V) произвольным образом на элементарные тела соответственно с объемамии выберем в каждом из них по точке. Примем приближенно, что в пределах элементарного телаплотность постоянна и равна плотностив выбранной точке. Тогда массакаждого элементарного тела приближенно выразится следующим образом:

,

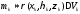масса же всего тела будет

.

В пределе, при стремлении к нулю наибольшего из диаметров d всех областей , это равенство делается точным, так что

, (2.1)

и задача решена.

Предел этого вида и есть тройной интеграл от функции по области . В принятых нами для них обозначениях полученный выше результат запишется так:

.

2.2. Определение тройного интеграла

Возьмем произвольную фигуру в пространстве, представляющую собойограниченную и замкнутую область. Условие существования объема для данной области в пространстве заключается в том, чтобы область была ограничена одной или несколькими гладкими поверхностями. В этом случае область называют кубируемой. В дальнейшем будем рассматривать только кубируемые области пространства.

ОПРЕДЕЛЕНИЕ 1. Ограниченная замкнутая область пространства называется телом.

Пусть в некотором теле задана функция. Разобьем это тело с помощью сети поверхностей на конечное число элементарных тел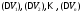соответственно с объемами. Выберем в каждом из них произвольным образом по точке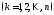. Значение функции в этой точкеумножим на объеми составиминтегральную сумму для функции 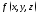по телу

. (2.2)

ОПРЕДЕЛЕНИЕ 2. Конечный предел интегральной суммы (2.2) при стремлении к нулю наибольшего из диаметровd всех элементарных тел называетсятройным интегралом функции в области , если он не зависит ни от способа разбиения телана элементарные тела, ни от выбора точекM_k в каждом из них:

.

Он обозначается символом .

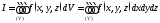Теорема 1. (необходимое условие существования тройного интеграла). Если функция интегрируема в ограниченной замкнутой области пространства, то она ограничена в этой области.

Теорема 2. (достаточное условие существования тройного интеграла). Если функция непрерывна в ограниченной замкнутой области пространства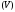, то она интегрируема в ней.

Из пункта 2.1. следует физический смысл тройного интеграла. Если функция 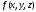есть плотность распределения массы по телу, то тройной интеграл от функциив областиравен массе этого тела:.