1.5. Вычисление двойных интегралов

1.5.1. Вычисление двойных интегралов в декартовых координатах

Определение 4. Областьназывается правильной в направлении оси ординат, если любая прямая, проходящая через внутренние точки областипараллельно оси ординат, пересекает границу этой области в двух точках.

Аналогично дается определение области, правильной в направлении оси абсцисс.

Следующие две теоремы позволяют вычислять двойные интегралы в декартовых координатах.

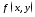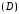ТЕОРЕМА 3. Если функция непрерывна в области, область- правильная в направлении оси ординат (рис. 1.4), то

.

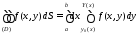ТЕОРЕМА 4. Если функция непрерывна в области, область- правильная в направлении оси абсцисс (рис. 1.5), то

.

Рисунок. 1.5

ПРИМЕР 1. Записать двойной интегралв виде

повторных интегралов (двумя способами), если:

а)область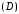ограничена прямымиx= 1,x= 2,y= 0,y= 4.

Решение

Построив на чертеже прямые, ограничивающие область интегрирования, видим, что представляет собой прямоугольник, стороны которого параллельны координатным осям (рис.1.6). В этом случае обе переменныеиизменяются в постоянных пределах, а формулы для вычисления двойного интеграла принимают соответственно вид:

= ;=.

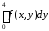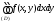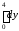
б)областьограниченна линиямиx= 0,x²+y²=r², причемx≥ 0,r> 0.

Решение

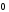Изобразим область интегрирования на чертеже (рис.1.7). Возьмем сначала постоянные пределы по переменной. Ими будут числаи. Для каждого значенияиз отрезкапринимает значения отдо.

Получим: .

Рисунок. 1.6 Рисунок. 1.7

Если постоянные пределы взять по , топринимает значения отдо. Получим:

.

Вообще при определении переменных пределов интегрирования полезно пользоваться следующим правилом: пусть изменяется в постоянных пределах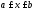(рис.1.8). Чтобы получить пределы интегрирования по, пересечем областьлучом, параллельным и одинаково направленным с осью ординат. Граница области, которую луч пересечет при входе в область, будет нижней границей этой области, а ее уравнение, решенное относительно, служит для установления нижнего предела интегрирования по.

Рисунок. 1.8

Граница области, которую луч пересекает, выходя из области, будет верхней границей этой области, а ее уравнение, решенное относительно , служит для установления верхнего предела интегрирования по.

Аналогичным образом при постоянных пределах по 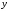определяются переменные пределы по.

ПРИМЕР 2. Записать двойной интегралв виде повторных интегралов (двумя способами), если область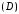– квадрат, ограниченный прямыми.

Решение

Строим на чертеже область интегрирования(рис.1.9). Пусть постоянны пределы интегрирования по. Ими будут –1 и +1. Проведем через областьлуч, параллельный и одинаково направленный с осью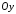. Как нижняя, так и верхняя границы области состоят из двух отрезков, пересекающихся соответственно в точках (0,–1) и (0,1).

Поэтому разобьем область на две части прямой. Тогда получим:

.

Рисунок. 1.9

Аналогично при выборе постоянных пределов по получим:

= +.

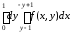ПРИМЕР 3.Изменить порядок интегрирования в повторном интеграле

Решение

Решение данной задачи состоит из двух частей:

а) восстановить область интегрирования (D) по известным пределам данного повторного интеграла;

б) записать повторный интеграл с постоянными пределами по yи переменными поx.

Так как внутренний интеграл взят по y, то, следовательно, пределы внутреннего интеграла получены из уравненийy= 2xиy= 2 –x. Это уравнения прямых, которые составляют какую-то часть границы области интегрирования (D). Изобразим прямые на чертеже (рис.1.10). Решая совместно уравненияy= 2xиy= 2 –x, найдем точку пересечения этих прямых. Так как дано, что абсциссаxточек области (D) изменяется в пределах от 0 до, то можно заключить, что искомой областью (D) является фигура, ограниченная линиямиx= 0,y= 2xиy= 2 –x.

Рисунок. 1.10

Расставляя теперь внешние пределы интегрирования по y, а внутренние поx, получаем:

+ .

ПРИМЕР 4. Изменить порядок интегрирования

+ .