2.3. Свойства тройного интеграла

1. .

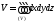2. Если умножить интегрируемую функцию в области на постоянную, то полученная функция также будет интегрируема, и при этом

.

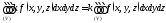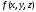3. Если в области интегрируемы функциии, то интегрируема и функция, причем

.

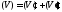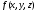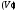4. Если в области задана функцияи область, то из интегрируемости функцииво всей областиследует ее интегрируемость в областяхи, и обратно – из интегрируемости функции в обеих областяхи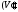вытекает интегрируемость в области. При этом

.

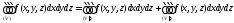5. Если для интегрируемых в областифункцийивыполняется неравенств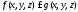о, то.

6. В случае интегрируемости функции 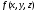интегрируема и функция, и имеет место неравенство.

7. Теорема О СРЕДНЕМ. Если функция непрерывна в области, то найдется такая точка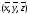в области, что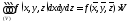, гдеV – объем области (V).

2.4. Вычисление тройных интегралов

2.4.1. Вычисление тройных интегралов в декартовых координатах

ОПРЕДЕЛЕНИЕ 3. Тело называется правильным в направлении осиOz, если выполняются два условия:

1) Любая прямая, проходящая через внутренние точки тела параллельно осиOz, пересекает границу тела в двух точках;

2) Область 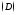, являющаяся проекцией тела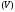на плоскость, является правильной в направлении хотя бы одной из осей координат.

Пусть тело представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностямии, проектирующимися на плоскость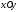в некоторую область, ограниченную кривой (K); с боков телоограничено цилиндрической поверхностью с образующими, параллельными осиOz, и с кривой (K) в роли направляющей (рис.2.1).

Рисунок. 2.1

Теорема3. Если дано тело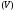, правильное в направлении осиOz; функция трех переменныхf(x,y,z) непрерывна в области, то

.

Если область 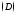представляет собой криволинейную трапецию, ограниченную двумя кривыми (рис.2.2)ии прямыми, то.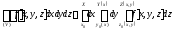

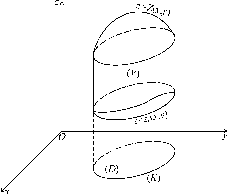
Рисунок. 2.2

Пример 1. Вычислить тройной интеграл, где областьограничена поверхностямиx+y+z= 1,x= 0,y= 0,z= 0.

Решение

Уравнение представляет собой плоскость, отсекающую на осях отрезки, равные 1;x= 0,y= 0,z= 0 - координатные плоскости. Областьесть пирамида (рис. 2.3).

Рисунок. 2.3

Из чертежа сразу видно, что по любой из переменных можно с одинаковым успехом брать постоянные пределы, и они равны 0 и 1. Возьмем, например, постоянные пределы по . Проекцией пирамиды на плоскостьявляется треугольник, ограниченный прямыми. Отсюда определяем пределы интегрирования по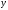. Для переменнойнижним пределом интегрирования будет, очевидно,(плоскость), а верхним – значение, полученное из уравнения плоскости, т.е.. Определив пределы интегрирования по каждой из переменных, можем представить данный тройной интеграл через повторный и выполнить вычисления, последовательно вычисляя соответствующие определенные интегралы. Получим:

= =

= ==

= ==

= ==–.

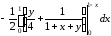Пример 2. Вычислить:, где телоограничено поверхностямиx= 2,y=,y= 0,z= 0,z= 2.

Решение

Выполним рисунок области интегрирования, ограниченной заданными в условии плоскостями (рис. 2.4).

Рисунок. 2.4 Рисунок. 2.5

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области (V)на выбранную плоскость изображена на рис. 2.5. Тогда исходный интеграл сводится к повторному с пределами интегрирования (рис. 2.5) по переменнойхот 0 до 2, поуот 0 до, и, в соответствии с рис. 1, по осиzот 0 до 2.

= ==

= 2= 2= 2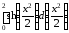= 2сh=

= 2(ch2 – 1).

Пример 3. Вычислить:, где тело (V) ограничено поверхностямиx= 2,y= 2x,y= 0,z= 0,z=xy.