1.6.2. Вычисление объемов тел

ПРИМЕР 1. Вычислить объем прямого бруса, ограниченного сверху параболоидоми имеющего основанием квадрат, ограниченный в плоскостипрямымиx= ±1,y= ±1.

Решение

Прежде всего, делаем чертеж (рис.1.24). В данном случае подынтегральной функцией будет 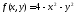. Она всюду положительна на указанном квадрате.

Рисунок. 1.24

Так как основанием бруса служит прямоугольник со сторонами, параллельными координатным осям OxиOy, то пределы интегрирования по обеим переменным постоянны. По формуле (1.2^*)

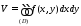
получим:

V====

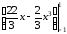= =–= 13.

Замечание. Задачу вычисления интеграла можно упростить, используя симметричность бруса относительно координатных плоскостейи, т.е. записав

.

ПРИМЕР 2.Вычислить объем шара, ограниченного сферой

.

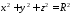Решение

В силу симметричности данного шара относительно координатных плоскостей, очевидно, достаточно ограничиться вычислением объема его восьмой части, расположенной в первой октанте (рис. 1.25).

Рисунок. 1.25

Подынтегральной функцией будет 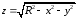(корень берем с положительным знаком потому, что рассматриваемая часть шара расположена над плоскостьюxOy).

Чтобы установить пределы интегрирования в формуле (1.2^*), необходимо сначала установить область интегрирования. Она ограничена пересечением плоскостиxOyс поверхностью шара. Чтобы получить это пересечение, положим в уравнении поверхности шараz= 0.

Полученная окружность и будет контуром области задания функции.

При нашем упрощении задачи областью интегрирования будет часть круга, расположенная в первой четверти плоскости xOy. Взяв постоянные пределы интегрирования поx (0 ≤x≤R), получим пределы поy: 0 – нижний,- верхний. По формуле (6) будем иметь:

.

Для вычисления внутреннего интеграла сделаем подстановку. Тогда и

(пока xпостоянная!). Следовательно,, откуда

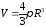
ЗАМЕЧАНИЕ. Можно было воспользоваться и переходом к полярной системе координат.

ПРИМЕР 3.Вычислить объем тела, ограниченного снизу плоскостью xOy, сверху плоскостью, с боков цилиндрической поверхностьюи плоскостью.

Рисунок. 1.26

Решение

Данное тело изображено на рисунке 1.26. Подынтегральная функция . Область интегрирования (D) ограничена прямойи параболой. При определении пределов интегрирования пользуемся уже известным приемом. Получими по формуле (1.2^*)

V===

= ==

= =.

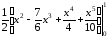ПРИМЕР 4.Оси двух круговых цилиндров с одинаковыми поперечными сечениями пересекаются под прямым углом. Вычислить объем общей части этих цилиндров.

Решение

Обозначим радиус поперечного сечения каждого из цилиндров через r. Выберем прямоугольную систему координат в пространстве таким образом, чтобы оси цилиндров совпадали с осямиOyиOz. Тогда уравнения цилиндрических поверхностей будут иметь вид: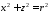- цилиндрическая поверхность с осью симметрииOy,- цилиндрическая поверхность с осью симметрииOz. На рисунке (1.27) отмечена одна восьмая часть тела, получаемого указанным сечением двух цилиндрических тел.

Рисунок. 1.27

Подынтегральной функцией будет, очевидно, разрешенное относительно yуравнение поверхности цилиндра с осью симметрииOy, т.е.. Проектируя ее часть, отрезанную второй поверхностью и содержащуюся в первом октанте, получим область интегрирования при вычислении объема выделенной на рисунке части тела. Ею будет часть круга, расположенная в первой четверти плоскостиxOy. Если поxвзять постоянные пределы (), то поy будут пределами: 0 - нижний предел, а- верхний. Тогда

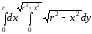= ==r³–=.

Следовательно,

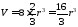
ПРИМЕР 5.Вычислить объем тела, ограниченного поверхностями