Решение

Криволинейный четырехугольник (D) изображен на рисунке 1.20. Обозначим новые переменные черезu иv. В системе координатuOv по условию задачи прямоугольник(Q) должен быть ограничен некоторыми прямыми, параллельными координатным осям,u = u₁,u = u₂,v = v₁,v = v₂. Из уравнений заданных линий

xy= 1,x–y= –1,

xy= 2,x–y= 1

видно, что при xy=u,x – y = v получится требуемое преобразование. Прямоугольник (Q) будет ограничен прямымиu= 1,u= 2,v= –1,v= 1 (рис. 1.21).

Рисунок. 1.20 Рисунок. 1.21

1.6. Приложения двойных интегралов к геометрии и механике

1.6.1.Вычисление площадей плоских фигур

ПРИМЕР 1.Вычислить площадь фигуры, лежащей в первом квадранте, ограниченной окружностьюx² +y² = 2ax, параболойy²= 2axи прямойx= 2a.

Решение

Прежде всего, необходимо данную фигуру изобразить на рисунке (рис.1.22).

Рисунок. 1.22

Для вычисления площади воспользуемся формулой: .

Из рисунка видно, что внешние пределы интегрирования удобнее выбрать по x, так как в противном случае фигуру пришлось бы разбивать на три части и соответственно вычислять три интеграла.

Постоянными пределами будут 0 и 2a. Снизу фигура ограничена верхней полуокружностью, уравнение которой. Следовательно,- нижний предел интегрирования. Сверху фигура ограничена верхней ветвью параболы, уравнение которой. Следовательно,- верхний предел интегрирования. Таким образом, получим:

ПРИМЕР 2.Найти площадь фигуры, ограниченной кривой

()

Решение

В данном случае, для того, чтобы представить на рисунке (рис.1.23) данную плоскую фигуру, необходимо предварительно провести исследование ее контура по заданному уравнению. Контур задан уравнением шестой степени относительно x иy.

В первую очередь отметим, что уравнение не меняется при замене yна-y, и потому кривая симметрична относительно оси абсцисс. Кроме того, из уравнения видно, чтоx≥ 0, и потому кривая расположена справа от оси ординат.

Рисунок. 1.23

Дальнейшее исследование методами дифференциального исчисления в данном случае весьма затруднительно, поэтому перейдем к полярным координатам, положив . Подставляя в (), получим:, или.

По этому уравнению видно, что каждому значению угла φ следует одно значение радиуса ρ. Кроме того, наибольшее значение ρ = 2 достигается при φ = 0, наименьшее – ρ = 0 при , т.е. при изменении φ от 0 довеличина ρ монотонно убывает от значения 2 до 0. Это дает возможность установить форму части кривой, расположенной в первой четверти. В силу симметричности кривой выясняется тем самым форма и всей кривой () (см. рис.1.22).

После того как выяснена форма заданной плоской фигуры и сделан чертеж, можно приступить к нахождению площади фигуры. Симметричность фигуры относительно оси Ox позволяет ограничиться вычислением площади ее части, лежащей в первой четверти. Получим¹:

S== 2= 2= 4=

= .

ПРИМЕР 3.Вычислить площадь параболического сегмента, ограниченного параболойи осьюOx.

Решение

Введем новые координаты, положив

, .

Тогда в системе координат uOvуравнение параболы примет обычный вид:u²=v(рис.1.24).

Рисунок. 1.24

Оси абсцисс (y= 0) в старой системе координат будет соответствовать в новой системе координат прямаяu=v.

Найдем якобиан преобразования:

.

При вычислении интеграла возьмем постоянные пределы интегрирования по u. Тогда переменными пределами поvбудут:u²– нижний,u– верхний. Таким образом, получим:

S======

= =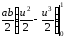