Решение

Так как, масса тела равна тройному интегралу от плотности:

m=,

следовательно, задача отыскания массы тела сводится к вычислению тройного интеграла от функции плотности по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.22).

Рисунок. 2.22 Рисунок. 2.23

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.23.

Так как одна из образующих поверхности тела – цилиндр, то удобнее перейти в цилиндрическую систему координат. Уравнения поверхностей в цилиндрической системе координат имеют вид:

μ = 5ρ²– функция плотности,

z=ρ– уравнение конуса,

ρ= 2 – уравнение цилиндра,

ρsinφ= 0 – уравнение плоскости,

z= 0 – уравнение плоскости.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.22) по переменной zот 0 доρ, по переменной ρ от 0 до 2, по φ от 0 до π (т.к. проекция на плоскостьxOy– верхняя часть окружности с радиусом равным 2, рис. 2.23). Тогда, с учетом якобиана перехода, имеем:

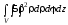= == 5=

= 5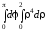= 5= 5= 32= 32= 32π.

Пример 8. Найти массу и момент инерции однородного тела, ограниченного поверхностямиx²+y²= 2zиx²+y²=z²относительно прямойx= 0,z= 4.

Решение

Проекцией данного тела, образованного пересечением параболоида вращения и конуса, на плоскость XOYявляется круг с центром в начале координат и радиусом 2.

Масса Мтела равна

М= ρ= ρ= 2πρ= 2πρ=.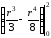

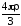Момент инерции Iданного тела найдем по формуле

I=,

где r– расстояние от точки (x,y,z) телаVдо прямойx= 0,z= 4. Квадрат этого расстояния находится по формулеr²=x²+ (z– 4)², поэтому

I= ρ= ρ=

= ρ=

= ρ=.

Пример 9. Найти координаты центра тяжести однородного тела, ограниченного поверхностямиx²+y²=zиx+y+z= 0.

Решение

Проекцией данного тела, образованного пересечением плоскости и параболоида вращения на плоскость XOYявляется областьD:x²+y²≤ –x–y, т.е. круг.

Поэтому в силу симметрии тела относительно плоскости x=yимеемx₀=y₀.

Положим x=rcosφ– 1/2,y=rsinφ– 1/2. Масса данного тела равна

M= ρ=ρ=

= ρ=

= 2πρ= 2πρ=.

Далее

x₀=y₀==

= =

= – = –,

z₀===

= =

= =.

Итак, координаты центра тяжести: x₀=y₀= –,z₀=.

Литература

1. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. [Текст] : учеб. пособие для вузов / Бугров Я.С., Никольский С.М. – М., Наука, 1997. – 446 с.

2. Высшая математика для экономистов. Под ред. Н.Ш.Кремера. [Текст] : учеб. пособие для вузов / Н.Ш.Кремер и др. – М., Банки и биржи, ЮНИТИ, 2003. – 470 с.

3. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты [Текст] : учеб. пособие / Кузнецов Л.А. – 4-е изд., стер. – СПб.: Лань, 2005. – 240 с.

4. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т. 2. [Текст] : учеб. пособие для вузов / Пискунов Н.С. – М.: Интеграл-Пресс, 2001. – 544 с.

5. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. [Текст] : учеб. пособие для вузов / Письменный Д.Т. – М.: Рольф, 2000. – 288 с.

6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 3. [Текст] : учеб. пособие для вузов / Фихтенгольц Г.М. – М., 1963 – 656 с.

7. Шипачев В.С. Высшая математика. [Текст] : учеб. пособие для вузов / Шипачев В.С. – М., Высшая школа, 2003. – 562 с.