Решение

а) Восстановим область интегрирования (D). Рассматривая оба слагаемых одновременно, заключаем, что нижний предел внутреннего интеграла на участках 0 ≤х≤ 1 и 1 ≤х≤ 3 выражается черезxодинаково: (парабола). Верхним же пределом на участке 0 ≤х≤ 1 является прямаяy=x, а на участке 1 ≤х≤ 3 - прямаяy= 1. Этого достаточно, чтобы построить область (D) (рис. 1.11).

Рисунок. 1.11

б) Из чертежа (см. рис. 1.11) видно, что постоянными пределами по yявляются числа 0 и 1. Нижним пределом измененияxбудетx=y, а верхним –x= 3. Корень берем с положительным знаком потому, что все точки области (D) имеют неотрицательные абсциссы. Искомый повторный интеграл представится в виде:

ПРИМЕР 5. Вычислить двойной интегралI=, где область (D) ограничена прямымиx= 0,y= 0,x+y= 1.

Решение

Область (D) изображена на рисунке 1.12.

Рисунок. 1.12

Возьмем постоянные пределы по переменной x, 0 ≤х≤ 1 . Тогда поyнижним пределом будетy= 0, а верхнимy= 1 –x. Получим:

I====

= ==.

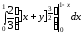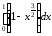1.5.2. Замена переменных в двойных интегралах

Предположим, что даны две декартовы плоскости с осями x,yиu,v. Рассмотрим в этих плоскостях две замкнутые области: область (D) на плоскостии областьна плоскости. Каждая из этих областей может быть и неограниченной, в частности может охватывать и всю плоскость. Границу области (если область не охватывает всей плоскости) будем предполагать кусочно-гладкой кривой.

Рисунок.1.13

Допустим, что в области дана система непрерывных функций

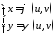_,(1.5)

которая устанавливает между областями (D) ивзаимно однозначное соответствие. Задание пары значений переменныхuиvиз областиоднозначно определяет некоторую точку в области (D) на плоскости(и обратно). Это дает основание и числаu,vназывать координатами точек области (D).

Кривую, составленную из точек области (D), у которых одна из координат сохраняет постоянное значение, называюткоординатной линией. В связи с тем, что координатные линии, вообще говоря, будут кривыми, числаu,v, характеризующие положение точки на плоскости, и в этом случае (как и в случае кривой поверхности) называюткриволинейными координатами точки.

Придавая координате uразличные (возможные для нее) постоянные значения, получим семейство координатных линий на плоскости. Фиксируя значение координатыv, получим другое семейство координатных линий. При наличии взаимно однозначного соответствия между рассматриваемыми областями различные линии одного и того же семейства не пересекаются между собой, и через любую точку области (D) проходит по одной линии из каждого семейства.

Вся сетка координатных линий на плоскости является изображением сетки прямыхu=constиv=constна плоскости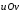(рис.1.13).

Далее будем предполагать, что функции (1.5) не только непрерывны, но и имеют непрерывные частные производные первого порядка.

Определение 5. Определитель второго порядка следующего вида

(1.6)

называют якобианом перехода от декартовых координат к криволинейным и обозначают .

Тогда формула перехода от декартовых координат к криволинейным координатам имеет следующий вид:

, (1.7)

≠0, за исключением конечного числа точек.

ЗАМЕЧАНИЕ 3. На практике декартовые координаты точки и ее криволинейные координаты рассматривают не на разных координатных плоскостях, а на одной совмещенной.

Простейшим и важнейшим примером криволинейных координат являются полярные координаты 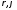. Они имеют наглядное геометрическое истолкование, как полярный радиус-вектор и полярный угол, но могут быть введены и формально, с помощью соотношений:

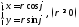. (1.8)

Если значения 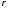иоткладывать по двум взаимно перпендикулярным осям, считая, скажем, - абсциссой, а - ординатой (при правой ориентации осей), то каждой точке полуплоскостипо указанным формулам отвечает одна определенная точка на плоскости.

Прямым отвечают круги радиуса с центром в начале (полюсе), а прямымотвечают лучи, исходящие из начала (полюса) под угломк оси(рис. 1.14).

Рисунок. 1.14

Однако в данном случае формулы преобразования не будут однозначно разрешимы: изменения величины угла на (гдеk– целое) не отразится на значенияхxиy. Для того чтобы получить все точки плоскости, достаточно ограничиться значениями ρ ≥ 0, 0 ≤ φ < 2π. Каждой точке (x,y), отличной от начала, отвечает одно значение ρ > 0 и одно значение φ в указанных пределах. Но неустранимое нарушение однозначности соответствия связано с началом координат: точкеx=y= 0 отвечает на плоскостився ось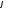(или, если угодно, отрезок ее отдо).

Формулы (1.8) называют формулами связи между декартовыми и полярными координатами.

Используя формулу (1.6), вычисляем якобиан перехода от декартовых координат к полярным:

===.

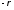Тогда, используя формулу (1.7), формула перехода от декартовых координат к полярным принимает следующий вид:

. (1.9)

ОПРЕДЕЛЕНИЕ 6. Область (D) называется правильной в направлении полярной оси, если луч, проходящий через внутренние точки области (D), пересекает границу области в двух точках (рис.1.15).

Рисунок. 1.15

Следующая теорема позволяет вычислять двойной интеграл в полярных координатах (см. замечание 3).

ТЕОРЕМА 5. Если функция непрерывна в области, область- правильная в направлении полярной оси(рис. 1.15), то

.

Тогда по формуле (1.9) получаем:

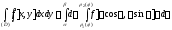
ПРИМЕР 1. Вычислить интеграл , где (D) – параллелограмм, ограниченный прямыми:x+y= 1,x+y= 2, 2x–y= 1, 2x–y= 3. (*)