Решение

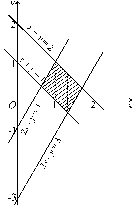
Рисунок. 1.16 Рисунок. 1.17

Изобразим область (D) на рисунке 1.16. Из рисунка видно, что для вычисления данного интеграла область (D) следует разбить на три части, как показано штриховыми линиями. Задача, таким образом, сводится к вычислению трех двойных интегралов. Однако можно избежать такого громоздкого способа решения, если ввести новые переменные, положив:

x+y=u, 2x–y=v. (**)

Тогда прямые x+y= 1,x+y= 2 в системе координатxOyпреобразуются в прямыеu= 1,u= 2 в системе координатuOv(рис. 1.17), а прямые 2x–y= 1, 2x–y= 3 преобразуются в прямыеv= 1,v= 3. Параллелограмм (D) преобразуется в прямоугольник (Q) со сторонами, параллельными координатным осям.

При преобразовании интеграла к новым переменным необходимо сначала получить выражения xиyчерезuиvиз равенств (*) и (**):

x=,y=.

Используя формулу (1.6) вычислим якобиан данного преобразования:

J(u,v) == ––= –.

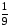Так как якобиан отличен от нуля, то выбранное преобразование области (D) в область (Q) будет взаимно однозначным. Кроме того, как функция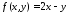, так и функции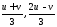вместе со своими частными производными являются непрерывными. Следовательно, по формуле (1.7) имеем:

Если подынтегральная функция или уравнение границы области интегрирования содержат сумму x²+y², то в большинстве случаев упрощение интеграла достигается преобразованием его к полярным координатам. Это объясняется тем, что данная сумма в полярных координатах получает весьма простое выражение

.

Если в состав подынтегральной функции или уравнения границы области интегрирования входит сумма вида ax²+by²;a> 0,b> 0, то пользуются «обобщенной» полярной системой координат:

.

Тогда ,

а якобиан преобразования в этом случае (убедится самостоятельно).

ПРИМЕР 2. Вычислить двойной интеграл, где (D) – верхний полукруг.

Решение

Преобразуем интеграл к полярным координатам:

.

Тогда x²+y²=ρ²,

= ,,

и данный интеграл примет вид:

= .

Рассмотрим область интегрирования (D) (рис. 1.18).

Рисунок. 1.18

Уравнение ее границы в полярных координатах примет вид:

ρ²cos²φ+ ρ²sin²φ= 1,

т.е. ρ²= 1, или ρ = 1 (предполагается, что полярная ось совпадает с положительным направлением оси абсцисс). В пределах данной области (D) полярный угол φ изменяется от 0 до π, а полярный радиус ρ изменяется в пределах от 0 до 1.

Следовательно,

I ===π=

=.

ПРИМЕР 3.Вычислить двойной интегралI=, где область (D) ограничена окружностямиx²+y²= 4x,x²+y²= 8xи прямымиy=x,y= 2x.

Решение

Область (D) изображена на рисунке 1.19. Перейдем к полярным координатамx=ρcosφ,y=ρsinφ. Тогда подынтегральная функция

f(x,y) ==ρ^-4.

Криволинейные участки границы области задаются уравнениями:

ρ²cos²φ+ ρ²sin²φ= 4ρcosφ, или ρ = 4cosφ,

ρ²cos²φ+ ρ²sin²φ= 8ρcosφ, или ρ = 8cosφ,

а прямолинейные участки уравнениями:

ρsinφ= ρcosφ, илиtgφ= 1, откуда φ =;

ρsinφ= 2ρcosφ, илиtgφ= 2, откуда φ =arctg2;

Итак, угол φ изменяется в постоянных пределах от доarctg2. Чтобы найти пределы изменения ρ, пересечем область (D) лучом, исходящим из полюса. При входе в область он пересечет границу ρ = 4cosφ, при выходе - границу ρ = 8cosφ. Следовательно, 4cosφ- нижняя граница интегрирования, а 8cosφ- верхняя граница.

Рисунок. 1.19

Имея в виду, что при данном преобразовании якобиан , можем представить двойной интеграл в новых координатах следующим образом:

I====

= ==.

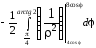ПРИМЕР 4. При какой замене переменных криволинейный четырехугольник (D), ограниченный линиямиxy = 1, xy = 2, x – y + 1 = 0, x – y – 1 = 0 (x > 0, y > 0), перейдет в прямоугольник (Q), стороны которого параллельны координатным осям?