
- •Федеральное агентство по образованию
- •1. Двойные интегралы
- •1.1. Задача об объеме цилиндрического бруса
- •1.2.Определение двойного интеграла
- •1.3. Свойства двойного интеграла
- •1.4. Сведение двойного интеграла к повторному интегралу
- •1.5. Вычисление двойных интегралов
- •1.5.1. Вычисление двойных интегралов в декартовых координатах
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •1.5.2. Замена переменных в двойных интегралах
- •Решение
- •Решение
- •Решение
- •Решение
- •1.6. Приложения двойных интегралов к геометрии и механике
- •1.6.1.Вычисление площадей плоских фигур
- •Решение
- •Решение
- •Решение
- •1.6.2. Вычисление объемов тел
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •1.6.3. Вычисление площадей поверхностей
- •Решение
- •Решение
- •1.6.4. Некоторые приложения двойных интегралов к механике
- •Решение
- •Решение
- •2.2. Определение тройного интеграла
- •2.3. Свойства тройного интеграла
- •2.4. Вычисление тройных интегралов
- •2.4.1. Вычисление тройных интегралов в декартовых координатах
- •Решение
- •Решение
- •Решение
- •2.4.2. Замена переменных в тройных интегралах
- •2.5. Приложения тройных интегралов
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Литература
- •Содержание
- •214013 Г. Смоленск, Энергетический проезд, 1
Решение
Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.
Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.16).

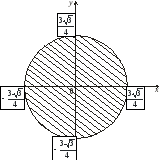
Рисунок. 2.16 Рисунок. 2.17
Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.17.
Так как одна из образующих поверхности тела – сфера, то удобнее перейти в сферическую систему координат. Уравнения поверхностей в сферической системе координат имеют вид:
ρ = 3 – уравнение сферы.
Уравнение конуса найдем следующим образом. Пусть х= 0, тогда:
z= ,
тогда
,
тогда ,
но
,
но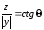 ,
,
после этого, с
учетом формулы приведения
 =
=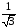 .
.
Решение тригонометрического уравнения, соответствующее условию задачи, имеет вид:
 –Θ =
–Θ =
 или Θ =
или Θ = .
.
Полученное решение является уравнением конуса в сферической системе координат.
Тогда исходный
интеграл сводится к повторному, с
пределами интегрирования (рис. 2.16) по
переменной Θ от 0 до
 ,
по переменной ρ от 0 до 3, по φ от 0 до 2π
(т.к. проекция на плоскостьxOy– окружность с единичным радиусом, рис.
2.17). Тогда, с учетом Якобиана перехода,
имеем:
,
по переменной ρ от 0 до 3, по φ от 0 до 2π
(т.к. проекция на плоскостьxOy– окружность с единичным радиусом, рис.
2.17). Тогда, с учетом Якобиана перехода,
имеем:
 =
=
 =
= =
=
=
 = 9
= 9 = 9
= 9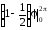 = 9·
= 9· ·2π
= 9π.
·2π
= 9π.
Пример 5. Найти объем тела, заданного ограничивающими его поверхностями:z= 5(x2+y2) + 2,z= 2 + 10y.
Решение
Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.
Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.18).


Рисунок. 2.18 Рисунок. 2.19
Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.19.
Так как одна из образующих поверхности тела – параболоид вращения, то удобнее перейти в цилиндрическую систему координат. Уравнения поверхностей в цилиндрической системе координат имеют вид:
z= 5ρ2+ 2 – уравнение параболоида вращения,
z= 2 + 10ρsinφ– уравнение плоскости.
Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.18) по переменной zот 5ρ2+ 2 до 2 + 10ρsinφ, по переменной ρ от 1 до 0, по φ от 0 до 2π (т.к. проекция на плоскостьxOy– окружность с единичным радиусом и с центром в точке (0, –1), рис. 2.19). Тогда, с учетом якобиана перехода, имеем:
 =
=
 =
=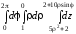 =
= =
=
=
 =
= =
=
=
 =
= =
=
=
 =
= .
.
Пример 6. Найти объем тела, заданного неравенствами:
9 ≤ x2+y2+z2≤ 81, 0 ≤z≤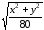 ,y≤ 0,y≤ –х.
,y≤ 0,y≤ –х.
Решение
Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.
Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.20).

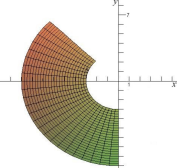
Рисунок. 2.20 Рисунок. 2.21
Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.21.
Рассмотрим первое двойное неравенство 9 ≤ x2+y2+z2≤ 81. Это пространство, заключенное между двумя сферами с радиусами 3 и 9, расположенными в начале координат.
Так как одна из образующих поверхности тела – сферы, то удобнее перейти в сферическую систему координат. Уравнения поверхностей в сферической системе координат имеют вид:
9 ≤ ρ ≤ 81 – сферы и пространство между ними.
Второе двойное
неравенство 0 ≤ z≤ задает пространство между плоскостьz= 0 и конусомz=
задает пространство между плоскостьz= 0 и конусомz=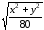 .
Уравнение плоскостиz= 0 в сферической системе координат
получим исходя из формул связи между
прямоугольной декартовой системой
координат и сферической:
.
Уравнение плоскостиz= 0 в сферической системе координат
получим исходя из формул связи между
прямоугольной декартовой системой
координат и сферической:
ρcosΘ= 0,
откуда ρ R,Θ= (без учета периода).
(без учета периода).
Уравнение конуса найдем следующим образом. Пусть х= 0, тогда:
z= .
.
Следовательно
 =
= .
.
Для решения тригонометрического уравнения воспользуемся формулами приведения:
ctg(Θ)
= .
.
Следовательно,
tg(Θ) = .
.
Полученное решение является уравнением конуса в сферической системе координат.
Отсюда, решение, соответствующее условию задачи, имеет вид:
Θ = arctg( ).
).
Полученное решение является уравнением конуса в сферической системе координат.
Следовательно, второе двойное неравенство, определяющее пространство между плоскостью и конусом, с учетом того, что угол Θ отсчитывается от оси zв направлении по часовой стрелке, имеет вид:
arctg( )
≤ Θ ≤
)
≤ Θ ≤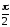 .
.
Третье y≤ 0 и четвертое неравенстваy≤ –хзадают полупространства, ограниченные соответствующими плоскостямиy= 0, ниже осих(отрицательные значенияу) иy= –х, ниже соответствующей плоскости, их проекции изображены на рис. 2.21.
Исходя из связи между декартовой и сферической системами координат, учитывая положительное направление отсчета угла φ, эти неравенства можно сразу записать в сферической системе координат:
φ ≥ π, φ ≤
 ,
,
Тогда исходный
интеграл сводится к повторному, с
пределами интегрирования (рис. 2.20) по
переменной Θ от arctg( )
до
)
до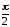 ,
по переменной ρ от 3 до 9, по φ от π до
,
по переменной ρ от 3 до 9, по φ от π до .
Тогда, с учетом якобиана перехода, имеем:
.
Тогда, с учетом якобиана перехода, имеем:
 =
=
 =
= =
=
 = 234
= 234 =
=
= 26 = 26
= 26 =
= .
.
ЗАМЕЧАНИЕ. Во время
вычисления интеграла возникает
необходимость вычислять cos(arctg( )).
Оно осуществляется с применением формулы
(справедливой только для положительных
значений аргументах):
)).
Оно осуществляется с применением формулы
(справедливой только для положительных
значений аргументах):
arctg х
= arccos ,
а cos(arccosx)
= x.
,
а cos(arccosx)
= x.
Пример 7. ТелоVзадано ограничивающими его поверхностями, μ – плотность. Найти массу тела.
x2+y2=z2,x2+y2= 4,y= 0,z= 0 (y≥ 0,z≥ 0); μ = 5(x2+y2).
