Решение

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностью и плоскостями (рис. 2.6).

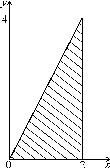
Рисунок. 2.6 Рисунок. 2.7

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция области (V)на выбранную плоскость изображена на рис. 2.7. Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.6) по переменнойхот 0 до 2, поуот 0 до 2x, и, в соответствии с рис. 1, по осиzот плоскостиz= 0 до «седла»xy.

= ===

= ====.

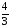
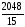2.4.2. Замена переменных в тройных интегралах

Идеи, развитые в пункте 1.5.2. в связи с преобразованием плоских областей, естественно переносятся и на случай пространственных областей.

Предположим, что даны два трехмерных пространства с системами координат xyz, иuvw. Рассмотрим в этих пространствах две замкнутые области: область (V) в пространствеи областьв пространстве, ограниченные соответственно поверхностямии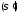, которые мы всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны между собойвзаимно однозначнымнепрерывным соответствием, которое осуществляется формулами:

, (2.3)

При этом необходимо, чтобы точкам поверхности отвечали именно точки поверхностии наоборот.

Пусть функции (2.3) имеют в области непрерывные частные производные.

Определение 4. Определитель третьего порядка следующего вида

(2.4)

называют якобианом перехода от декартовых координат к криволинейным и обозначают .

Числа , однозначно характеризующие положение точки в пространствеxyz, называютсякриволинейными координатами этой точки. Точки пространстваxyz, для которых одна из этих координат сохраняет постоянное значение, образуюткоординатную поверхность. Всегда будет существовать три семейства таких координатных поверхностей; через каждую точку области (V) проходит по одной поверхности каждого семейства.

Тогда формула перехода от декартовых координат к криволинейным координатам будет иметь следующий вид:

. (2.5)

ЗАМЕЧАНИЕ 1. На практике рассматривают не два координатных пространствах, а одно совмещенное.

а) Цилиндрические координаты представляют соединение полярных координат в плоскостис обычной декартовой аппликатойz(рис. 2.8).

Рисунок. 2.8

Формулы, связывающие их с декартовыми координатами, имеют вид

.

Эти формулы отображают область 0 ≤ ρ < +, 0 ≤ φ < 2π, –<z< +на все пространствоxyz. Отметим, однако, что прямаяотображается в одну точку (0,0,z); этим нарушается взаимная однозначность соответствия. Координатные поверхности в рассматриваемом случае будут:

а) - цилиндрические поверхности с образующими, параллельными оси; направляющими для них служат окружности на плоскостис центром в начале;

б) - плоскости, проходящие через ось;

в) 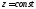- плоскости, параллельные плоскости.

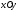По формуле (2.4) получаем якобиан преобразования:

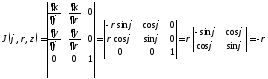, (2.6)

а формула перехода (2.5) принимает вид

. (2.7)

б) Сферические координатысвязаны с декартовыми формулами:

, (2.8)

где .

Геометрический смысл величин ясен из рисунка 2.9:rесть радиус-векторOM, соединяющий начало с данной точкойM;- угол, составляемый этим радиус-вектором с осьюOz;- угол, составляемый с осьюOxпроекциейрадиус-вектораOMна плоскостьxOy.

Рисунок. 2.9

Координатные поверхности составляют три семейства:

а)- концентрические сферы с центром в начале координат;

б) - круговые конусы, осью которых служит осьOz;

в) - плоскости, проходящие через осьOz.

По формуле (2.4) получаем якобиан преобразования:

,(2.9)

а формула перехода (2.5) принимает вид

. (2.10)