Решение

Поверхность 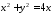есть круговой цилиндр, ось которого совпадает с осьюOz, аи- плоскости, проходящие через осьOyпод разными углами наклона к плоскостиxOy. Эти плоскости, пересекая цилиндр, вырезают из него клинообразный слой (рис.1.28), объем которого и требуется вычислить.

Рисунок. 1.28

Сам слой не является цилиндрическим брусом, и потому его объем не может быть вычислен непосредственно по формуле (1.2^*). Однако его можно рассматривать как разность двух цилиндрических брусов, срезанных сверху плоскостямии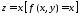. Пределы изменения дляxиyнаходим из уравнения контура области интегрирования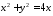. Здесь удобнее взять постоянные пределы по. Тогда поyбудут: 0 – нижний предел,- верхний предел, и искомая половина объема тела представится в виде:

Следовательно, V= 8π.

1.6.3. Вычисление площадей поверхностей

ПРИМЕР 1.Вычислить площадь той части плоскости, которая заключена в первом октанте (рис.1.29).

Рисунок. 1.29

Решение

Имеет место формула

. (1.10)

Мы имеем: и

.

Проекцией данной плоскости на плоскость xOyявляется треугольник, ограниченный координатными осямиOx,Oyи прямой(последняя получается из уравнения данной плоскости приz= 0). Получим:

S====== 14.

ПРИМЕР 2.Вычислить площадь части поверхности, вырезанной цилиндром.

Решение

Контуром проекции вырезанной части на плоскость xOyявляется лемниската(рис.1.30).

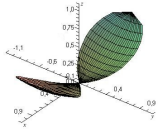
Рисунок. 1.30

Цилиндр вырезает из параболоида два равных куска поверхности. Чтобы вычислить их общую площадь, воспользуемся формулой (1.10). Для нее из уравнения параболоида получим подынтегральную функцию.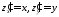,. Следовательно,. Преобразуем интеграл к полярным координатам. Подынтегральная функция запишется в виде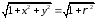, а уравнение лемнискаты – в виде, или.

Так как параболоид и цилиндр симметричны относительно плоскостей xOz,yOz, то достаточно вычислить интеграл по одной четвертой части лемнискаты, расположенной в первой четверти плоскостиxOz. Следовательно, пределами интегрирования будут:. Получим:, откуда.

1.6.4. Некоторые приложения двойных интегралов к механике

ПРИМЕР 1.Найти массу квадратной пластинки со стороной 2a, если плотность материала пластинки пропорциональна квадрату расстояния от точки пересечения диагоналей и на углах квадрата равна единице.

Решение

Пластинку естественно расположить в прямоугольной системе координат таким образом, чтобы точка пересечения диагоналей совпадала с началом координат, а стороны были параллельны координатным осям (рис. 1.31).

Масса плоской фигуры вычисляется по формуле

_{где -}плотности распределения массы по плоской фигуре.

Если плоская фигура однородная, то есть величина постоянная.

Рисунок. 1.31

После этого можно составить функцию плотности материала пластинки по условиям задачи. ПустьM(x,y) – произвольная точка квадрата. Тогда квадрат расстояния от точки пересечения диагоналей (начало координат) будет равен. Следовательно, плотность в точкеMпредставится в виде, гдеk– коэффициент пропорциональности. Чтобы найти числовое значение этого коэффициента, используем известное значение плотности на углах квадрата. Возьмем, например, вершину угла (a,a). Тогда получим: 1 =k (a²+a²), откуда.

Подставляя найденное значение kв выражение функции плотности, окончательно получим: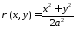. Теперь остается только вычислить двойной интеграл.

Учитывая, что подынтегральная функция четная относительно xиy(т.е. плотность симметрична относительно начала координат), можем ограничиться вычислением интеграла только по одной четвертой части области (D), расположенной в первой четверти

m==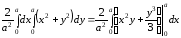

= ===.

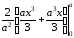ПРИМЕР 2.Найти статические моменты относительно осей координат сегмента эллипса, ограниченного прямой(рис. 1.32).