1.2.Определение двойного интеграла

Возьмем произвольную фигуру на плоскости, представляющую собойограниченнуюизамкнутуюобласть. Ее границу мы всегда будем представлять в виде замкнутой кривой (или нескольких таких кривых).

Определение 2. Областьназывается квадрируемой, если она имеет площадь.

Замечание 1. В дальнейшем будем рассматривать только квадрируемые области.

Пусть в области определена функция двух переменных. Разобьем областьсетью кривых наконечное число элементарных областейсоответственно с площадями. В каждой элементарной областивозьмем по произвольной точке, значение функции в этой точке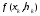умножим на площадьсоответствующей области и все подобные произведения сложим. Полученную сумму

(1.3)

будем называть интегральной суммой для функции f (x, y) по области (D).

Обозначим через наибольший из диаметров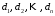элементарных областей.

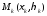Определение 3. Если при стремлении к нулю наибольшего из диаметровсуществует конечный пределинтегральной суммы (1.3), и он не зависит ни от способа разбиения областина элементарные области, ни от выбора точекв каждой элементарной области, то этот предел называетсядвойным интегралом отфункции по областии обозначается.

Теорема1. (необходимое условие существования двойного интеграла). Если функцияинтегрируема в ограниченной замкнутой области, то она ограничена в этой области.

Теорема2. (достаточное условие существования двойного интеграла). Если функциянепрерывна в ограниченной замкнутой области, то она интегрируема в ней.

Из пункта 1.1. следует геометрический смысл двойного интеграла. Если функциянеотрицательна:- и интегрируема в области, то двойной интеграл от функциипо областиравен объему тела, сверху ограниченного поверхностью,cбоков - цилиндрической поверхностью с образующими, параллельными оси, снизу – областьюна плоскости:.

1.3. Свойства двойного интеграла

1. .

2. Если функцию , интегрируемую в области, умножить на постояннуюk, то полученная функцияk f (x,y) также будет интегрируема в области, причем

.

3. Если в области интегрируемы функциии, то интегрируема и функция, причем

.

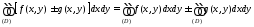4. Если область , в которой задана функция, кривойразделена на две областии, то из интегрируемости функции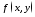во всей областиследует ее интегрируемость в областяхи, и обратно – из интегрируемости функции в обеих областяхивытекает ее интегрируемость в области. При этом

.

5. Если для интегрируемых в области функцийивыполняется неравенство, то.

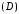6. В случае интегрируемости функции в областиинтегрируема и функция |f(x,y)| в области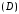, и имеет место неравенство.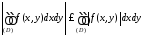

7. ТеоремаО СРЕДНЕМ. Если функция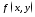непрерывна в области, то найдется такая точкав области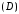, что=f·S_D, гдеS_D– площадь областиD.

ЗАМЕЧАНИЕ 2. Свойство 3 обобщается на любое конечное число функций.

Свойство 4 обобщается на любое конечное число областей.

1.4. Сведение двойного интеграла к повторному интегралу

Продолжая трактовать двойной интеграл геометрически, как объем цилиндрического бруса, дадим указания относительно его вычисления путем сведения к повторному интегралу.

Ранее рассматривалась задача вычисления объема тела по его поперечным сечениям. Напомним относящуюся сюда формулу. Пусть тело ограничено плоскостямии(рис.1.2).

Рисунок. 1.2

Допустим, что сечение тела плоскостью, перпендикулярной к оси абсцисс и отвечающей абсциссе , имеет площадь. Тогда объем тела, в предположении его существования, выразится формулой

. (1.4)

Применим теперь эту формулу к вычислению объема цилиндрического бруса, о котором шла речь выше. Начнем с простого случая, когда в основании бруса лежит прямоугольник [a,b;с,d] (рис.1.3).

Рисунок. 1.3

Сечение бруса плоскостью есть криволинейная трапеция. Для нахождения ее площади спроектируем эту фигуру на плоскость. Получим конгруэнтную с ней трапецию(ибо проектирование происходит без искажения). Но уравнение линиина плоскости, очевидно, будет.

Пользуясь известным выражением площади криволинейной трапеции в виде определенного интеграла, будем иметь . Так как наше рассуждение относится к любому сечению, то вообще для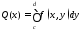. Подставляя это значение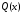в формулу (1.4), получим. Но мы имеем для объемаи выражение (1.2*), следовательно,- двойной интеграл приведен к повторному.

Аналогичный результат можно получить и для общего случая, когда область 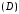на плоскостипредставляет собой криволинейную трапецию, ограниченную двумя кривыми: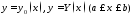и двумя прямымии(рис. 1.4). Разница по сравнению с рассмотренным случаем состоит в следующем: раньше при любом фиксированнымизменениепроисходило в одном и том же промежутке, а теперь этот промежутоксам зависит от, так что

.

Окончательно получим: .

Рисунок. 1.4