2.5. Приложения тройных интегралов

1. Вычисление объема

V=.

2. Масса тела

m=,

где ρ(x,y,z) – плотность распределения масс в произвольной точке тела (V).

3. Статические моменты

M_xy=,

M_zx=,

M_yz=,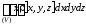

M_z=.

4. Моменты инерции тела относительно осей координат

I_x=,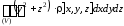

I_y=,

I_z=.

5. Координаты центра тяжести тела

X_c=,

Y_c=,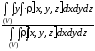

Z_c=.

Пример 1. Найти объем тела, заданного ограничивающими его поверхностями:

x= 5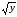,x=,z= 0,z+y=.

Решение

Воспользуемся следующей формулой для вычисления объема тела:

V=. (2.11)

Таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.10).

Рисунок. 2.10 Рисунок. 2.11

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.11. Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.11) по переменнойyот 0 до(так как область не является простой относительно плоскостиxOz), поxотдо 5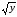, и, в соответствии с рис. 1 по осиzот плоскостиz= 0 до плоскостиz=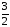–y.

= ===

= ==

= =.

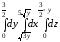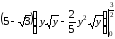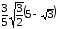Пример 2. Найти объем тела, заданного ограничивающими его поверхностями:x²+y²– 2x= 0,z= 7 – 4y²,z= 1.

Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.12).

Рисунок. 2.12 Рисунок. 2.13

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.13.

Так как одна из образующих поверхности тела – цилиндр, то удобнее перейти в цилиндрическую систему координат. Уравнения поверхностей в цилиндрической системе координат имеют вид:

ρ²– 2ρcosφ= 0,z= 7 – 4ρ²sin²φ,z= 1.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.12) по переменной zот 1 до 7 – 4ρ²sin²φ, по переменной ρ от 0 до 1, по φ от 0 до 2π (т.к. проекция на плоскостьxOy– окружность с единичным радиусом, рис. 2.13). Тогда, с учетом якобиана перехода, имеем:

= ===

= ==

= ==+=

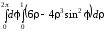= += 5π.

Пример 3. Найти объем тела, заданного ограничивающими его поверхностями:y= –x²+ 3,y= 2,z= 1 –x²+ 2y²,z= 5 –x²+ 2y².

Решение

Воспользуемся формулой (2.11) для вычисления объема тела и, таким образом, задача отыскания объема тела сводится к вычислению тройного интеграла по соответствующей фигуре.

Выполним рисунок области интегрирования, ограниченной заданными в условии поверхностями (рис. 2.14).

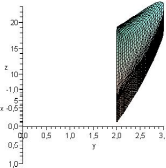
Рисунок. 2.14 Рисунок. 2.15

Область является правильной относительно всех осей. Проектируем тело на плоскость xOy. Проекция областиVна выбранную плоскость изображена на рис. 2.15.

Тогда исходный интеграл сводится к повторному, с пределами интегрирования (рис. 2.15) по переменной yот 2 до –х²+ 3, поxот –1 до 1, и, в соответствии с рис. 1 по осиzот гиперболического параболоидаz= 1 –x²+ 2y²до такого же точно гиперболического параболоида, смещенного по осиzна четыре единицы вверхz= 5 –x²+ 2y².

= ===

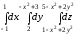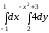4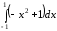= 4= 4·=.

Пример 4. Найти объем тела, заданного ограничивающими его поверхностями:z=,z=.