Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика

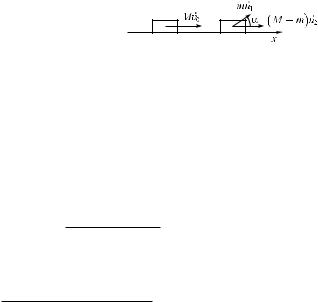
¹ 6. Железнодорожная платформа с установленным на ней орудием движется горизонтально со скоростью v0 = 1 м/с. Масса платформы вместе с орудием Ì = 2 · 104 кг. Из орудия выпускается снаряд по ходу платформы со скоростью u1 = 800 м/с под углом = 30° к горизонту. Масса снаряда m = 20 кг. С какой скоростью u2 будет двигаться платформа после выстрела?

Решение

Схематический чертеж с указанием импульсов тел системы до и после выстрела, а также системы отсчета приведен на рисунке. Запишем закон сохранения импульса в векторной форме:

Спроецируем полученное уравнение на координатную ось:

(M – m)v0 + mv0 = (M – m)u2 + mu1cos .

Затем разрешим данное уравнение относительно u2:

u2 Mv0 mu1cos . M m

Подставляя исходные данные, получим:

u2 2 104 1 20 800 0,866 0,308 ì/ñ. 2 104 20

¹ 7. Люстра весом 98 Н висит на цепи, которая выдерживает нагрузку 196 Н. На какой максимальный угол можно отклонить люстру от положения равновесия, чтобы при последующих колебаниях цепь не оборвалась (сопротивлением воздуха пренебречь)?

Решение

Колебания люстры будут происходить по дуге окружности, таким

271

Нормальное (центростремительное) ускорение связано со скоростью известной формулой: an v 2 r, ãäå r , — длина нити. Тогда уравнение (2) перепишем в виде

Из треугольника ÀÂÑ (см. рисунок): BC AB cos cos , тогда

272

h cos 1 cos .

Высоту поднятия h подставим в уравнение (4) и найдем :

Fí mg 2mg 1 cos ,

cos 3mg Fí , 2mg

cos 0,5; 60°.

¹ 8. Колесо автомобиля радиусом 0,4 м, имеющее массу 10 кг, раскручено до частоты вращения 60 об/мин и предоставлено самому себе. Под действием трения вала колеса о подшипники оно остановилось че- рез 1 мин 20 с. Определить момент силы трения вала колеса о подшипники и работу силы трения.

Решение

Используем основное уравнение динамики вращательного движения

Ìt = I2 – I1,

ãäå Ì — тормозящий момент; t — время действия тормозящего момента; I — момент инерции колеса; 2 — конечная угловая скорость; 1 — на- чальная угловая скорость. Решая уравнение относительно Ì, получим:

M 0,8(0 6,28) 0,0628 Í·ì, 80

где знак «минус» означает, что момент Ì — тормозящий.

273

Работа силы трения может быть вычислена по формуле A M , где — угловое перемещение колеса (угол поворота колеса от начального момента до полной остановки). Вычислим по формуле

A0,0628 251,2 15,8 Äæ.

¹9. Материальная точка массой m = 0,01 кг совершает гармониче-

ские колебания по закону синуса с периодом Ò = 2 с и начальной фазой 0, равной нулю. Полная энергия колеблющейся точки W = 0,1 мДж. Требуется: найти амплитуду À колебаний; написать закон данных колебаний x = f(t); найти наибольшее значение силы Fmax, действующей на точку.

Решение

Запишем закон гармонических колебаний: x = A sin t. Так как закон не дает возможности определить амплитуду À, обратимся к условию зада- чи и воспользуемся полной энергией W. Полная энергия колеблющейся точки Å равна, например, ее максимальной кинетической энергии Wê.max:

W Wê.max mvmax2 .

2

Скорость v колеблющейся точки можно определить, взяв первую производную смещения õ по времени v dxdt A cost, ãäå vmax = A. Подставим значение vmax в формулу для энергии W mA2 2 2, найдем амплитуду колебаний:

Выразим амплитуду через период Ò, учитывая, что 2:

T

274

Напишем закон гармонических колебаний для данной точки:

õ = 0,045sint.

Взяв первую производную скорости по времени, можно найти ускорение колеблющейся точки:

a dv A 2 sint. dt

Максимальное ускорение (при sint = 1) |amàõ| = A 2.

Из второго закона Ньютона следует, что максимальная сила

|Fmax| = ma = mA 2.

Произведем вычисления: Fmax = 0,01 · 0,045 · 3,142 Í = 4,44 · 10–3 Í.

¹10. Вода движется в трубе диаметром d1 2,5 см со скоростью

v1 1 м/с. В трубу врезан кран диаметром d2 1 см. Определить стои-

мость воды, вытекшей из крана за 1 ч, если цена 1 м3 воды равна 16 руб.

Решение

Для установившегося потока несжимаемой жидкости справедливо условие неразрывности струи:

ãäå v2 — скорость вытекания струи воды из крана:S1 èS 2 — соответственно площади сечения трубы и крана, которые вычисляются по формулам:

Из формулы (1) следует:

275

ãäå t — время вытекания воды. Подставив в формулу (4) соответствующие выражения из (2) и (3), получим:

V d1 d2 v1 t. 4

Тогда стоимость вытекшей воды

N16V 4 d1 d2 v1 t 4 3,14 0,025 0,01 1 3600 11,3 ðóá.

¹11. Определить число N молекул воды, содержащихся в объеме V = 1 ìì3, и массу ò1 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекулы.

Решение

Число N молекул, содержащихся в некоторой массе m, равно произведению числа Авогадро NA на количество вещества : N N A . Так как количество молей вещества m , где — молярная масса, то

Nm N A . Выразив в этой формуле массу как произведение плотности

3,34 · 1019 молекул.

Массу одной молекулы можно найти делением молярной массы на число Авогадро: m1 N A . Подставив сюда числовые значения и NÀ,

276

Если молекулы воды плотно прилегают друг к другу, то можно счи- тать, что на каждую молекулу приходится объем (кубическая ячейка) V1 = d3, ãäå d — диаметр молекулы. Отсюда

Объем V1 найдем, разделив молярный объем V на число молекул в моле, т. е. на число Авогадро NA:V1 V NA . Подставим полученное выражение для V1 в формулу (2): d 3V NA .

Входящий в эту формулу молярный объем определяется выражением V = / . Тогда искомый диаметр молекулы

Подставим числовые значения физических величин в формулу (3) и произведем вычисления:

¹ 12. В баллоне объемом V = 10 л находится гелий под давлением ð1 = 1 МПа при температуре Ò1 = 300 К. Для надувания воздушных шариков из баллона было использовано ò = 10 г гелия, при этом температура в баллоне понизилась до Ò2 = 290 К. Определить давление ð2 гелия, оставшегося в баллоне.

Решение

Для решения задачи воспользуемся уравнением Менделеева — Клапейрона, применив его к конечному состоянию газа:

ãäå ò2 — масса гелия в баллоне в конечном состоянии; — молярная масса гелия (см. справочные таблицы в приложении или таблицу Д. И. Менделеева); R — универсальная газовая постоянная. Из уравнения (1) выразим искомое давление p2:

277

Массу гелия ò2 выразим через массу гелия в начальном состоянии ò1 и массу m гелия, взятого из баллона:

Массу ò1 найдем также из уравнения Менделеева — Клапейрона, применив его к начальному состоянию:

Подставляя выражения (3) и (4) последовательно в формулу (1), найдем:

или после преобразования и сокращения:

Выразим величины, входящие в эту формулу, в единицах СИ: ð1 = 1 ÌÏà = 106 Ïà, m = 10 ã = 10–2 êã, V = 10–2 ì3. Произведем вычисления:

¹ 13. Для принятия водных процедур в ванну было набрано 80 л горячей воды при температуре tâ = 80 °С. Сколько льда, взятого при температуре të = –10 °С, надо добавить в ванну, чтобы температура смеси стала комфортной, т. е. tê = 40 °Ñ.

Решение

При добавлении льда в ванну лед сначала нагревается до температуры плавления (tïë = 0 °С), а затем плавится, превращаясь в воду. Полу- чившаяся изо льда вода нагревается до конечной температуры tê = 40 °Ñ.

278

Лед и получившаяся из него вода поглощают тепло, которое отдает горя- чая вода, изначально находившаяся в ванной. Уравнение теплового баланса в этом случае можно записать в виде

где первое и третье слагаемые в левой части описывают соответственно процессы нагрева льда и воды, получившейся изо льда; второе слагаемое в левой части равенства описывает процесс плавления льда; в правой части уравнения стоит выражение для количества теплоты, отданного горячей водой. В уравнении (1) стоят разности температур, а сами температуры можно брать в градусах Цельсия. Сделаем преобразования и выразим из (1) массу льда:

Значения удельных теплоемкостей воды câ , ëüäà cë , удельной теплоты плавления льда , температуры плавления льда tïë и плотности воды â берутся из справочных таблиц (см. приложение).

Подставим числовые значения в формулу (2) и произведем вычисле-

íèÿ:

4200 1000 0,08 80 40

mâ 2100 0 10 335000 4200 40 0 25,6 êã.

¹ 14. Кислород массой ò = 2 кг занимает объем V1 = 1 ì3 и находится под давлением p1 = 0,2 MПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 ì3, а затем при постоянном объеме до давления p3 = 0,5 МПа. Считая кислород идеальным газом, найти изменение его внутренней энергии U, совершенную им работу À и теплоту Q, переданную кислороду. Построить график процесса в координатах PV.

Решение

Качественно график процесса, происходящего с газом, представлен на рисунке. На участке 1–2 с кислородом происходит изобарный процесс, при котором изменяется внутренняя энергия газа и газ совершает положительную работу. На участке 2–3 с кислородом происходит изо-

279

хорный процесс, который также сопровождается изменением внутренней энергии, но работа при этом равна нулю.

Полное изменение внутренней энергии газа в процессе 1–2–3 определяется изменением температуры и выражается формулой

ãäå i — число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5); — молярная масса кислорода (см. справочные таблицы (см. приложение) или таблицу Д. И. Менделеева).

Полная работа в процессе 1–2–3 равна работе расширения газа при постоянном давлении, которая определяется выражением

Температуру газа в точках 1, 2 è 3 найдем из уравнения Менделеева — Клапейрона:

Подставляя данные в задаче значения в выражение (3) и выполняя арифметические действия, получим:

Подставляя в выражение (1) и (2) числовые значения величин, найдем:

280