1.4.2. Решение слау методом Гаусса

1) Метод Гаусса

Этот метод базируется на методе элементарных преобразований.

Элементарные преобразования для слау включают в себя:

1)) Перестановку строк

2)) Умножение строки на число отличное от нуля

3)) Прибавление к элементам строки другой строки, умноженной на некоторое число.

Рассмотрим этот метод на примере (его смысл: сведение левой части к диагональному виду).

Пример:

Решение примера приведённого выше методом Гаусса в матричной форме

A B E X

~~~

2. Теорема Кронекера – Капелли

Теорема 1.4.1

Если у системы (1.4.1) ранг основной матрицы равен рангу расширенной матрице rang A = rang , (1.4.11)

то система (1.4.1) совместна то есть имеет решение (нетривиальное).

Доказательство.

Система (1.4.1) в матричной форме имеет вид:

x₁ + x₂ + … +x_n

Если решение существует, то матрица-столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит переход А не изменяет её ранга, т.е. rang A = rang _{. Э}то означает, что они имеют один и тот же базисный минор. Если же rang A 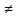rang _{, т.е} А и имеют различный базисный минор, то это означает, что матрица-столбец свободных членов не есть линейная комбинация столбцов матрицы А и значит система не имеет решения.

1.4.3 Решение слау с помощью обратной матрицы

Решение системы при помощи обратной матрицы справедливо для СЛАУ (1.4.5)

Пусть(1.4.12)(1.4.13)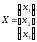(1.4.14)

В этом случае систему можно записать так: (1.4.15)

= (1.4.16)

Решим систему (1.4.15) в матричной форме для этого помножим левую и правую часть на А^-1, тогда получим

(1.4.17) 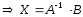(1.4.18)

(1.4.19)

Пример.

Х = ,B = ,A =

Решение

Найдем обратную матрицу А^-1.

 = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.

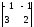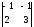M₁₁ = = -5; M₂₁ = = 1; M₃₁ = = -1;

M₁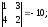₂ = M₂₂ = M₃₂ =

M₁₃ = M₂₃ = M₃₃ =

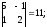
A^-1 = ;

Проверка

AA^-1 = =E.

Найдём матрицу Х:

Х = = А^-1В = = .

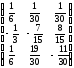
Ответ: x =1; y = 2; z = 3.

Лекция 5

Тема 1.5. Однородные, неопределённые и несовместные системы линейных алгебраических уравнений (слау)

1.5.1. Решение однородных СЛАУ.

1.5.2.Решение неопределённых СЛАУ.

1.5.3. Определение несовместных СЛАУ.

1.5.1. Решение однородных слау.

1)Основные понятия

Определение 1.5.1.

Система вида (1.5.1) называется однородной СЛАУ.

Замечание: если для (1.5.1), то эта система имеет единственное и притом тривиальное решениеx₁ = x₂= ... = x_n =0.

2. Решение однородных СЛАУ

Теорема 1.5.1.

Если основная матрица А системы (1.5.1) имеет порядок n, а ее r=rangA<n, то система (1.5.1) имеет n-r независимых решений.

Определение 1.5.2.

Совокупность независимых решений системы (1.5.1) называется фундаментальной системой решений.

Пример 1:

detA=0

Решение:

~~~;;

n - r = 3 – 2 = 1.

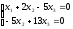
Пример 2:

Найти фундаментальную систему решений однородной СЛАУ.

Решение.

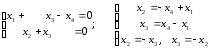
Ответ: x₁ = k, x₄ = l, x₂ = k - l, x₃ = l – k.