3.1.3. Методы интегрирования

1. Интегрирование методом замены переменной.

Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от неё, т.е. если ∫ f(x) dx = F(x) + c, то и

∫ f(u) du = F(u) + c, (3.1.4)

где u=φ(x) – любая дифференцируемая функция от х.

Примеры

1. ∫(5х+1)²dx ===

=

2.

3.

4.

2. Интегрирование некоторых функций, cодержащих квадратный трехчлен

1. 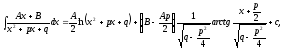(3.1.5)

2. (3.1.6)

3. (3.1.7)

4. (3.1.8)

3) Интегрирование методом деления по частям

∫ udv = uv - ∫ vdu (3.1.9)

Типовые примеры

1. = =,,,=

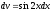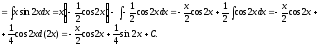
2. =,,,=

=,,,

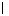
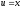3.

Лекция 16.

Тема 3.2. Интегрирование рациональных и тригонометрических функций.

3.2.1. Интегрирование рациональных дробей.

3.2.2. Интегрирование иррациональных функций.

3.2.3. Интегрирование тригонометрических функций.

3.2.1. Интегрирование рациональных дробей.

1)Рациональные дроби

Рациональной дробью называется дробь вида , (3.2.1.)

где P_m(x) – полином m-й степени и Q_n(x) – полином n-й степени. Если в формуле (3.2.1) m < n, то дробь называется правильной, если m ≥ n, то – неправильной. Неправильная рациональная дробь может быть путем деления числителя на знаменатель, разложена на алгебраический полином и правильную рациональную дробь.

Пример:

Правильные рациональные дроби могут быть разложены на элементарные.

2)Элементарные рациональные дроби.

Элементарными дробями называются дроби вида:

I (3.2.2),II (3.2.3),III (3.2.4),IV (3.2.5)

3) Интегрирование элементарных дробей

I 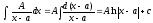(3.2.6)

II (3.2.7)

III

(3.2.8)

IV 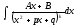(3.2.5) – вычисляется с помощью рекурентных формул.

Примеры.

1.

2.

4) Интегрирование рациональных дробей.

1. Метод неопределенных коэффициентов.

Решение:

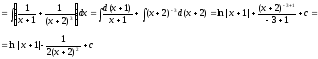
2. Метод произвольных коэффициентов.

Решение:

3.2.2. Интегрирование иррациональных функций.

Примеры.

1.

2.

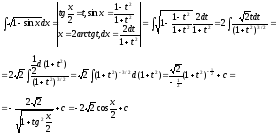
3.

= =

=

4.

3.2.3. Интегрирование тригонометрических функций.

Вспомогательные формулы:

sin cos = [sin(+) + sin( −)],

cos cos = [cos(+) + cos( −)],

sin sin = [cos(−) − cos( +)]

Примеры.

1. 

2. 

3. 

Лекция 17

Тема 3.3. Определенный интеграл.

3.3.1. Определенный интеграл. Теорема существования. Основные свойства определенного интеграла.

3.3.2. Формула Ньютона – Лейбница.

3.3.3. Методы интегрирования.

3.3.1. Определенный интеграл. Теорема существования. Основные свойства определенного интеграла.

1) Интегральная сумма

Если функция f(x) определена на отрезке x Є [a; b] и a = x₀ < x₁<…<x_n=b – произвольное разбиение отрезка на n частей, то сумма вида:

S_n = , (3.3.1)

где , называется интегральной суммой.

2) Определенный интеграл

Определенным интегралом называется предел интегральной суммы (3.3.1) вида: (3.3.2)

3)Теорема существования

Теорема 3.3.1.

Если функция f(x) непрерывна на отрезке [a;b] или имеет на этом отрезке конечное число точек разрыва первого рода, то она интегрируема на этом отрезке.

4)Основные свойства определенного интеграла

1. (3.3.3)

2. (3.3.4)

3. 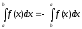(3.3.5)

4. Если на [a, b] f(x) < φ(x), то и <

5. Если m – наименьшее значение функции f(x) на [a, b], а М – наибольшее значение, то m(b-a) < <M (b-a) (3.3.6)

6. Если функция f(x) непр. на [a, b], то найдется такая точка ζ Є [a,b], что будет справедливо следующее равенство : 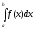=f(ζ) (b-a) (3.3.7)

Это свойство интерпретируется как Теорема о среднем.

Теорема 3.3.2.

Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке существует точкатакая, что

Доказательство

В соответствии со свойством 5:

т.к. функция f(x) непрерывна на отрезке [a,b], то она принимает на этом отрезке все значения отmдо М. Другими словами, существует такое число[a,b], что если

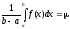и=f(), аab, тогда.

Теорема доказана.

7) Для произвольных чисел a,b,cсправедливо равенство:

(3.3.8)

Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.

8) (3.3.9)