Лекция 3
Тема 1.3. Обратная матрица.
1.3.1. Понятие обратной матрицы.
1.3.2. Получение обратной матрицы с помощью присоединенной матрицы.
1.3.3. Получение обратной матрицы методом элементарных преобразований.
1.3.1.Понятие обратной матрицы.
1) Вырожденная и невырожденная матрицы.
Определение 1.3.1.
Квадратная матрица А называется вырожденной, если detA=0 и невырожденной, если detA≠0.
2) Обратная матрица.
Определение 1.3.2.
Невырожденная матрица А-1 называется обратной к невырожденной матрице А, если для нее выполняется условие:
А-1А=АА-1=Е (1.3.1)
Теоремы существования и единственности обратной матрицы.
Теорема 1.3.1. (т. существования обратной матрицы)
Для того, чтобы матрица А-1, являющаяся обратной матрицей по отношению к матрице А, существовала, необходимо и достаточно, чтобы матрица А была невырожденной.
Доказательство:
Необходимость - Пусть А-1 существует. Требуется доказать, что А – невырожденная. Док-во:
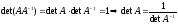
А-1
– существует, следовательно, она не
вырожденная, т.е.
ч.т.д.
Достаточность
- Пусть
А – невырожденная. Требуется доказать,
что А-1
существует. Док-во:
ч.т.д.
Следствие. Всякая невырожденная матрица имеет обратную, и наоборот, если матрица имеет обратную, то она не вырожденная.
Теорема 1.3.2. (т. единственности обратной матрицы)
Если матрица а имеет обратную матрицу а-1, то она единственная.
Свойства операций обращения матриц.
1) (АВ)-1=В-1А-1
2) (А-1)-1=А
1.3.2. Получение обратной матрицы с помощью присоединенной матрицы.
1) Присоединенная матрица.
Определение 1.3.3.
Невырожденная
матрица Аυ
называется присоединенной по отношению
к невырожденной матрице А, если она
является транспонированной по отношению
к А и состоит из алгебраических дополнений
Пример:
Свойства присоединенной матрицы:
2) Получение присоединенной матрицы с помощью алгебраических дополнений.
Пример:
,
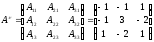
3) Получение обратной матрицы с помощью присоединенной матрицы.
Теорема 1.3.3.
Обратная матрица равна присоединенной матрице, умноженной
на
,
т.е.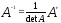
(1.3.2)
Доказательство:
ч.т.д.
Пример:
,
А-1=?
Проверка: АА-1=Е
1.3.3. Получение обратной матрицы методом элементарных преобразований.
Пример:
Решение:
A
E
E A-1
Лекция 4
Тема 1.4. Система линейных алгебраических уравнений (слау)
1.4.1. Решение СЛАУ методом Крамера
1.4.2. Решение СЛАУ методом Гаусса
1.4.3. Решение СЛАУ с помощью обратной матрицы
1.4.1.Решение слау методом Крамера.
1) Основные понятия
Определение 1.4.1.
Система
уравнений вида
, (1.4.1)
где
-
произвольные постоянные, а
-
переменные и
- постоянные называется системой.
Определение 1.4.2.
Матрица
, (1.4.2)
составленная
из коэффициентов при неизвестных в
системе (1.4.1) называется матрицей
коэффициентов или основной матрицей
системы, а матрица В=
, (1.4.3)
называется матрицей столбцом свободных членов.
Определение 1.4.3.
Матрица
(1.4.4)
называется расширенной матрицей системы
(1.4.1)
Замечание: Особую роль в теории СЛАУ играют системы у которых количество неизвестных равно количеству уравнений т.е. m=n
(1.4.5),
для такой системы
(1.4.6), а матрица столбец свободных
членов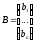
(1.4.7.).
2) Метод Крамера
Замечение: Метод Крамера применим лишь для СЛАУ вида (1.4.5)
1)) Метод Крамера для системы 2-х уравнений с 2-мя неизвестными.
|
|
_______________________
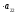
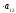
отсюда
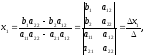
В
данном случае формула для
(1.4.8)
2)) Метод Крамера для системы с n уравнениями и n неизвестными.
(1.4.9)
(1.4.10)
Пример: решить систему методом Крамера
Решение:
,
,
x1=1, x2=2, x3=3